Knowledge Discovery Process
Through the lens of Information Theory
What is a Knowledge Discovery Process?
Uncertainty isn’t just a hurdle. It's a mirror reflecting how much (or how little) we truly understand about our problem, our customers, and the solutions they need.
So, how do we tackle it? By discovering what we don't know. Yes, discovering - not merely learning.
The process of knowledge discovery is a journey of exploration and investigation, as an individual seeks to fill in the gaps in their understanding and gain the knowledge necessary to complete a task.
The process of knowledge discovery starts with identifying the knowledge to be discovered, which can be thought of as the question "what do we need to know?" This represents the gaps in understanding or information that an individual or group believes they lack. By recognizing what is unknown, i.e., the questions without answers, the process of knowledge discovery aims to fill in these gaps by finding answers through research, investigation, and other means.
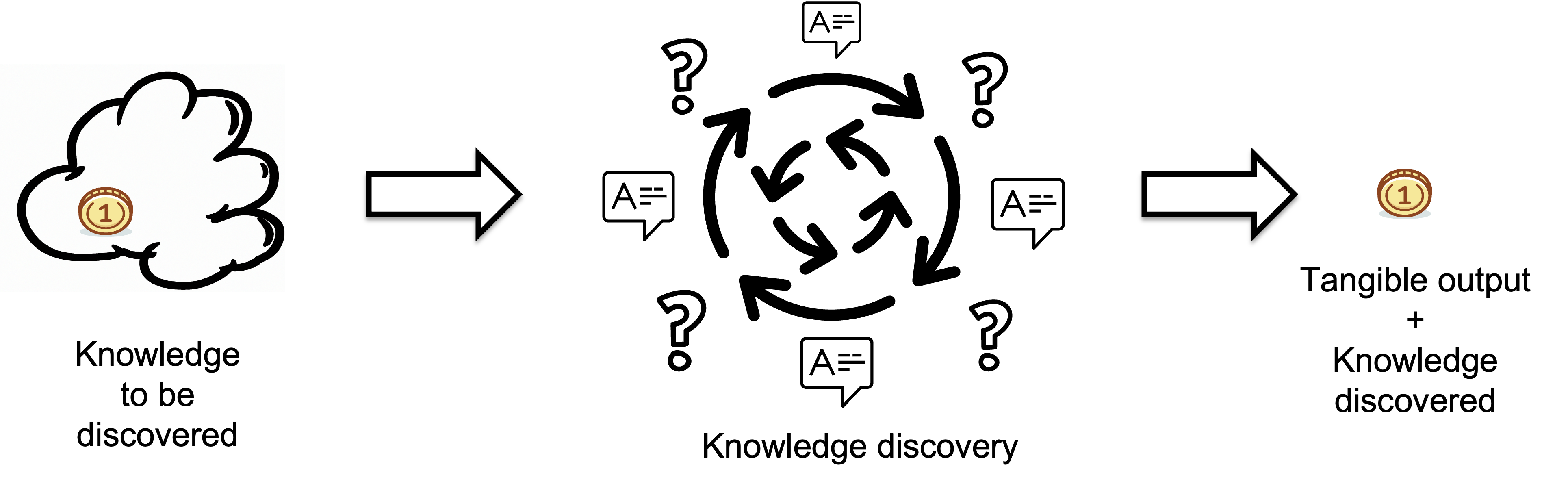
The tangible output represents the knowledge discovered through the knowledge discovery process, encapsulating the new information that has been acquired. In contrast, the input represents the missing information or knowledge that needs to be discovered.
We do not address the question of the quality of the tangible output, assuming that it meets appropriate standards.
We consider the knowledge discovery part as a black box, and we don't know how it produces tangible output in response to input questions. This black box may contain a human or an AI tool, such as ChatGPT.
Knowledge to Be Discovered
Let's delve into the world of knowledge acquisition and decision-making through a focused scenario: a person is tasked with typing the first letter of a word. This situation offers a window into how decisions are influenced and made based on available knowledge and external information sources. In this context, we define key variables to navigate the process:
- X: Represents the aggregate of all information, insights, and understanding required to achieve a specific outcome. X encompasses a broad spectrum of possible outcomes, signifying the overarching objective of the decision-making process — identifying the correct letter to type.
- Y: Represents the person's existing knowledge base, encompassing all prior information relevant to making the decision about X, as well as any other knowledge about anything else. Y influences the initial state of certainty or uncertainty regarding X, acting as the foundation upon which decisions are based. Initially, Y holds a certain level of information that may or may not be sufficient to resolve the uncertainty about X.
- Z: An external source of information, such as a book, from which the person can obtain answers to binary questions that directly pertain to X. Each interaction with Z is aimed at reducing the uncertainty about X. Z is a mechanism through which Y is enhanced, enabling a more informed decision-making process.
Given the multiple potential outcomes represented by X, there is a certain level of entropy H(X) associated with X, which signifies the initial uncertainty about X before considering any existing knowledge Y. H(X) is more about the potential variety and unpredictability in X itself, rather than the person's specific state of knowledge at any given moment. From a knowledge-centric perspective, H(X) is the person's perception of the "required knowledge" to successfully complete the task,
The mutual information I(X;Y) quantifies how much Y reduces the person's uncertainty about X due to the information obtained from Y It also captures the variability in the utility of Y. From a knowledge-centric perspective, the mutual information I(X;Y) is the person's perception of their individual capabilities or their "prior knowledge". It is the part of the person's existing knowledge base Y that they consider applicable for successfully achieving the outcome X. Prior knowledge is known to facilitate the learning of new knowledge from knowledge sources like Z. Estimates suggest that between 30% and 60% of the variance in learning outcomes can be explained by prior knowledge[1]. Additionally, prior knowledge of different domains can jointly support the recall of arguments[2]. In instances where no questions are needed, Y has effectively reduced all uncertainty about X by itself, suggesting high mutual information I(X;Y) for those instances. Conversely, when questions are needed, Y has not fully reduced uncertainty about X, indicating lower mutual information I(X;Y) for those specific instances. The overall I(X;Y) would reflect an average across all instances, considering both when Y is and isn’t sufficient by itself.
Questions are the cognitive tools we use to close knowledge gaps. Questions arise only when there is Knowledge to Be Discovered. The existence of any question implies a perceived gap in knowledge, understanding, or certainty. Whether the gap is large (fundamental knowledge is missing) or small (details need confirmation or alternatives are being explored), the act of questioning reflects the Knowledge work i.e. the effort to bridge that gap. Conversely, if an individual believes they know everything necessary about a task, there is no uncertainty, and no questions arise.
For each task, Required Knowledge represents the complexity of the task, i.e. what must be known to complete it, while Prior Knowledge refers to the skills, experience, and understanding an individual already possesses. The gap between these two is the Knowledge to Be Discovered. It represents what the individual thinks they don't know, given what they think they do know. It is the information that the individual is missing about the task before engaging with it. That is the challenge they face. Any uncertainty or need for additional clarity about a task implies the existence of some form of a knowledge gap - even if it is small or subtle.
If an individual believes they know everything they need to know about a task, there would be no questions. Any uncertainty or need for additional clarity about a task implies the existence of some form of a knowledge gap - even if it is small or subtle. Even when someone has sufficient knowledge to perform a task, there can still be a small knowledge gap that prompts questions. For example, a developer asking for a more efficient algorithm assumes there's room for improvement, revealing a gap (though minor). So, it’s fair to say that questions always indicate some level of missing knowledge, even if it's negligible. Confirmation or clarification reflects a gap in certainty rather than a lack of explicit knowledge. Even when someone knows how to perform a task, they might seek assurance or alignment with others, indicating they perceive some uncertainty. As you noted, this still reflects a form of a gap—however narrow. Exploring alternatives or expanding knowledge explicitly indicates a desire to bridge a gap in possibilities. While the original task might not require this knowledge, the individual perceives value in acquiring it, confirming the presence of a gap related to optimization or optionality.
Conditional Entropy H(X|Y) quantifies the uncertainty that remains about X after considering the prior knowledge I(X;Y) before augmentation through Z. It represents the "knowledge to be discovered" - needed to complete a task.
In practical terms, this means observing whether, in a specific instance, they need to ask further questions (indicating some remaining uncertainty about X) or if Y alone was enough to make the decision (no remaining uncertainty about X). Thus, H(X∣Y) can be understood or estimated based on the person's experience in each instance — how often and under what conditions they find Y sufficient or insufficient. The person will experience H(X∣Y) directly through the necessity of asking questions to reduce uncertainty. Over many instances, our observations about when and how often Y is sufficient could inform an estimate of H(X∣Y), and indirectly, the nature of H(X) itself by aggregating our experiences across different contexts or states of knowledge (Y).
Knowledge Discovered
The knowledge discovered during a task refers to the information that is gained by an individual through their engagement in that task, and is the nformation that has been verified and confirmed through investigation or experience to allow the individual to successfully complete the task.
Below is an animated example of calculating Knowledge Discovered when we search for a gold coin hidden in 1 of 64 boxes.
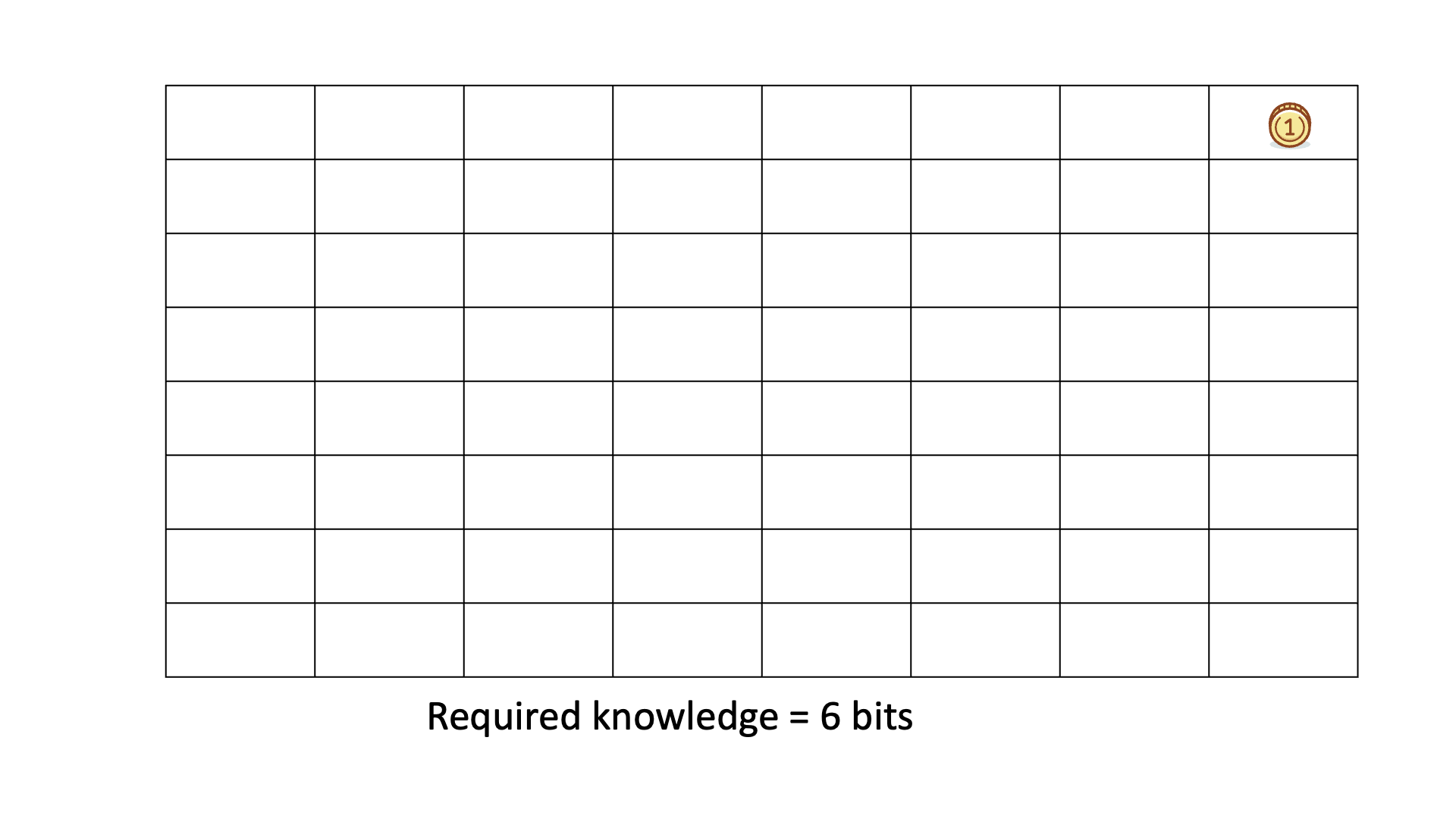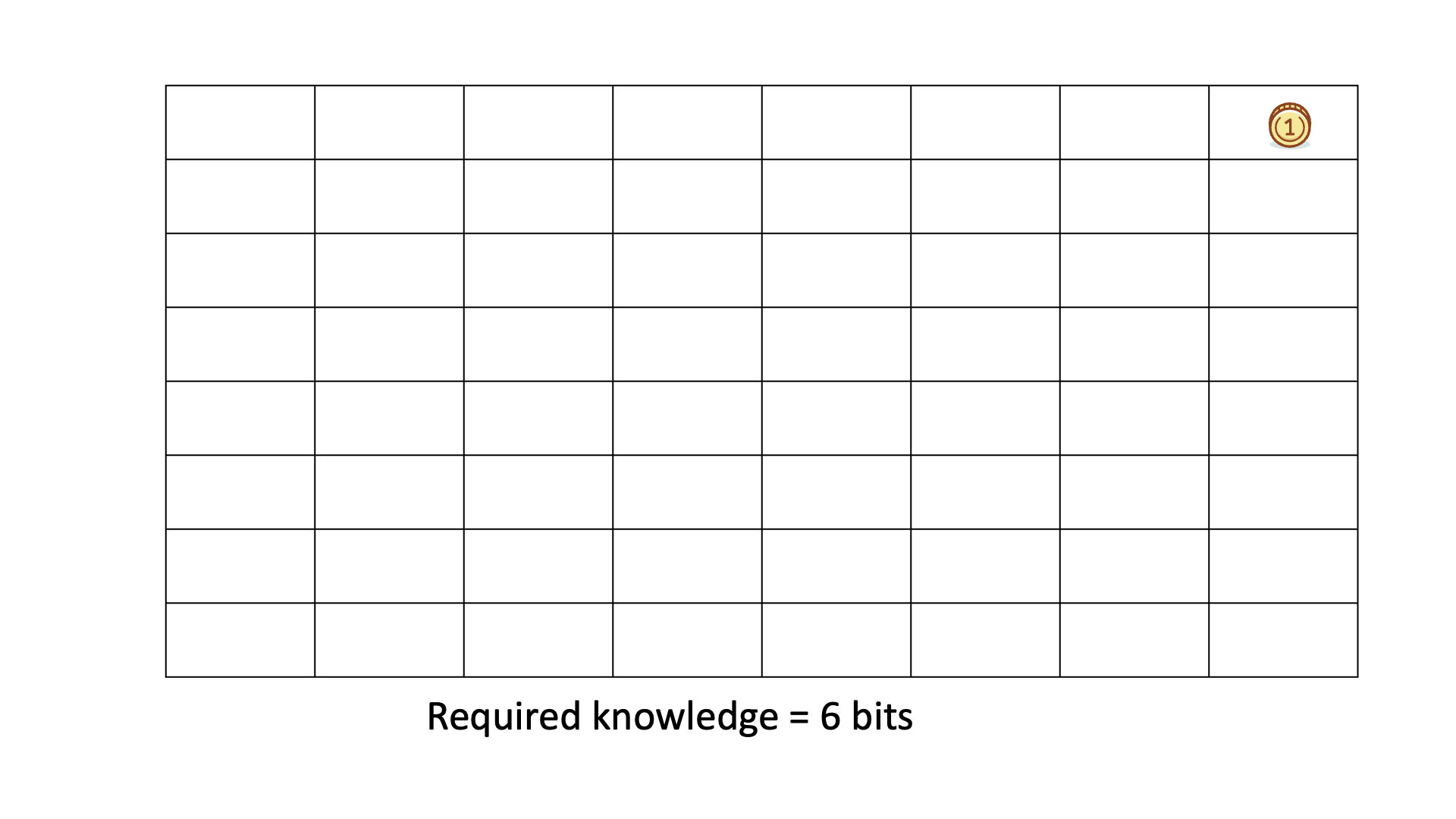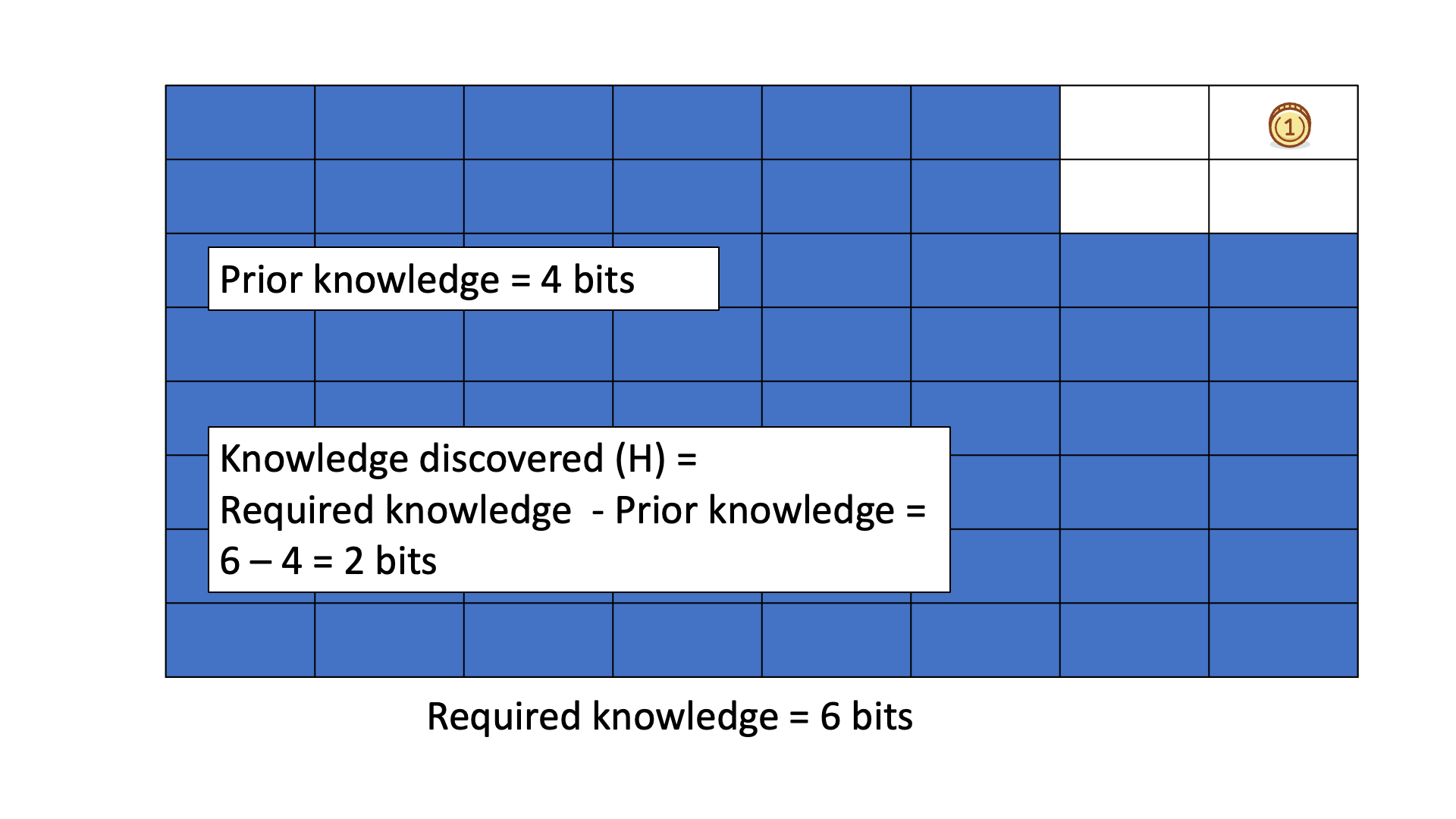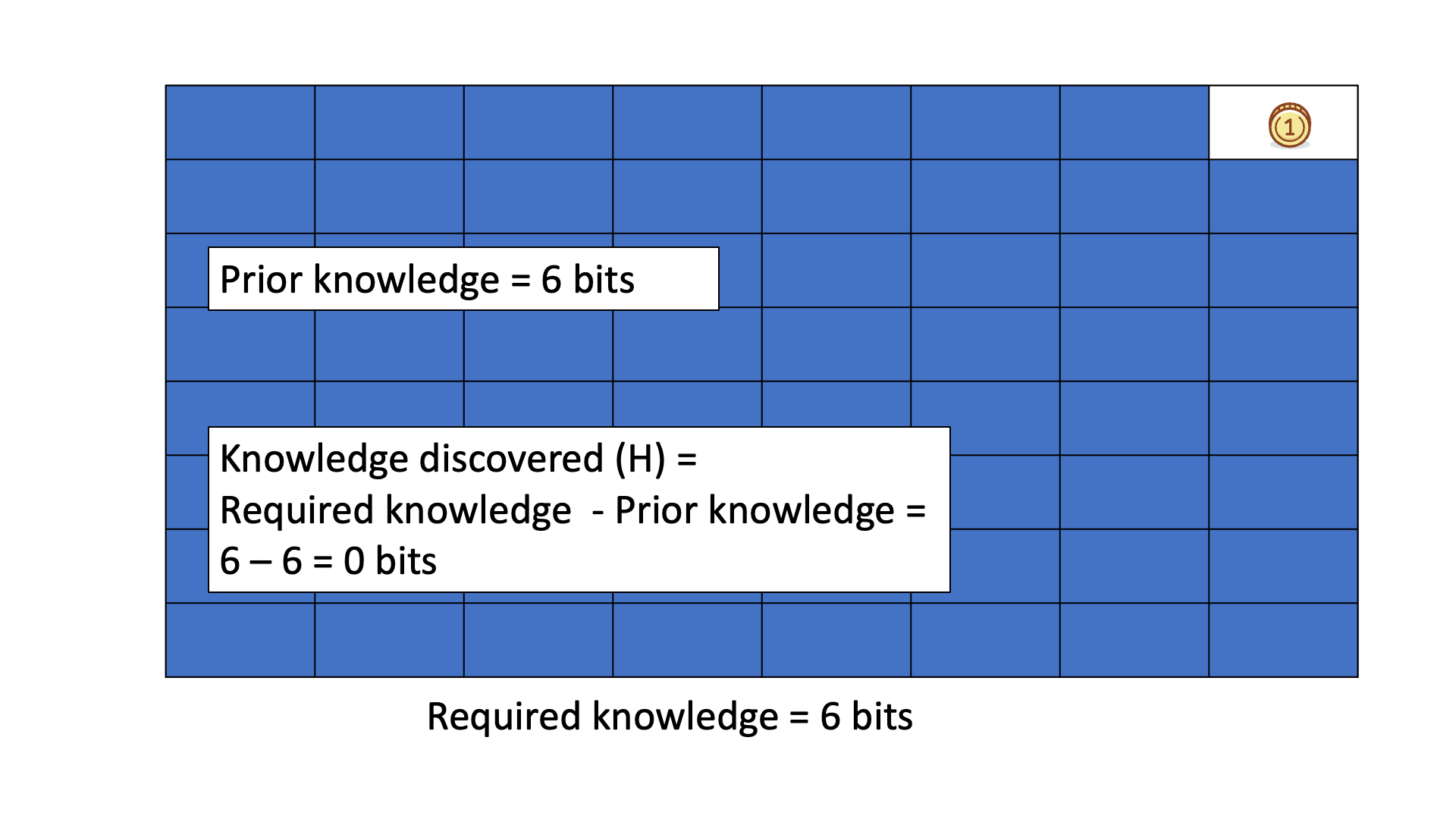
This knowledge can be considered real as it has been tested and validated. However, the knowledge to be discovered, which represents the gap in understanding or the information that is believed to be missing, may not always be real. The distinction between knowledge to be discovered and knowledge discovered can be seen in games such as "20 questions" and ""Surprise 20 questions" where the knowledge to be discovered is an object or concept that is not certain until it is guessed or revealed.
Knowledge is a dynamic construct shaped by human inquiry, creativity, and interaction. It evolves through the systematic refinement of conjectures and the elimination of errors, evolving toward greater understanding. To measure knowledge, we interpret knowledge through the perspective of information theory. In the table below, we have related human terms to concepts from information theory.
| SUBJECTIVE | OBJECTIVE (ACTUAL) | ||
|---|---|---|---|
| Human perspective | Information Theory lens | Human perspective | Information Theory lens |
|
Knowledge to be discovered |
Knowledge discovered |
||
|
Required knowledge |
|
|
|
|
Prior knowledge |
|
|
|
The first column of the table lists various subjective elements from both human and information theory perspectives. The second column of the table contains knowledge discovered, which is the information that can be observed and verified through objective reality. We can measure knowledge discovered (or the information gained) by counting the number of questions asked.
It is not possible to accurately measure the knowledge to be discovered in advance as demonstrated by the concept of ""it from bit"".
However, If the task is completed successfully, it can be inferred that the knowledge discovered during the process is equal to the knowledge that was deemed necessary to be discovered to complete the task. In other words, all the information and understanding required to complete the task has been obtained.
Discovering knowledge
The diagram below illustrates the internal workings of a knowledge discovery process.
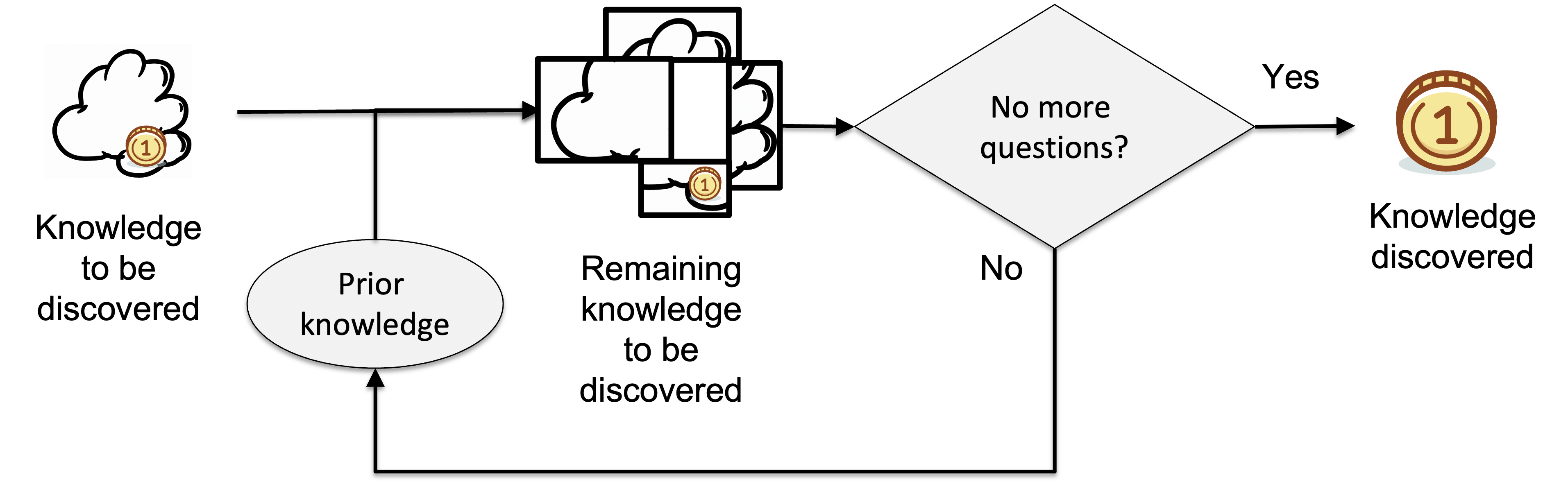
The input to the process is the knowledge required to successfully complete the task at hand, which is represented as a cloud with a gold coin inside. The knowledge discovery process aims to uncover the gold coin, which represents the knowledge that is essential to complete the task.
When prior knowledge is applied and used to group the possible states and decide on the number of states in each class, we can say that an understanding of the knowledge to be discovered has been gained. This knowledge to be discovered is represented by missing information, measured in bits. The result is the remaining knowledge to be discovered, which still contains some missing information.
If the remaining missing information is greater than zero, the discovery process continues by applying prior knowledge and gathering new information from the world through various methods such as active perception, monitoring, testing, experimenting, exploring, and inquiry, as explained here.
If the remaining missing information is zero, the discovery process is considered complete, and the required knowledge has been discovered. The knowledge discovered is confirmed, and the process can be stopped.
Dynamic Process of Knowledge Discovery
Initially, Y may or may not be sufficient to resolve X i.e. not knowing the letter to type, As the person encounters uncertainty about X they engage in a process of querying Z to obtain specific information that addresses this uncertainty. Each query to Z is formulated as a binary question, the answer to which directly reduces the uncertainty about X by one bit of information. The key aspect of this scenario is that as the person receives answers from Z, their knowledge base (Y) is incrementally augmented, enhancing their capability to make an informed decision about X.
- Incremental Increase in I(X;Y): With each piece of information acquired from Z and integrated into Y, there is a corresponding increase in the mutual information I(X;Y). This reflects a reduction in the uncertainty about X due to the enhanced state of Y.
- Reduction of H(X∣Y) H(X∣Y) quantifies the remaining uncertainty about X given the current state of knowledge Y. As Y is augmented with each answer from Z, the uncertainty about X decreases. Therefore, the process of augmenting Y effectively reduces H(X∣Y) because Y becomes increasingly informative about X.
This process highlights a dynamic view of knowledge discovery, where Y is not static but evolves through interaction with Z. The evolving state of Y and its impact on decision-making about X can be modeled as a sequence of updates, each contributing to a gradual increase in I(X;Y) and decrease in H(X∣Y). Eventually the uncertainty about X is reduced to zero.
Let's look at a numerical example of this knowledge discovery process. Say we observe the person and notice they asked 3 binary questions to determine the letter they need to type,
Initial State (Before Asking Questions):
- Entropy (H(X)): We don't know the value of H(X), because it depends on the context of the decision to be made (i.e., the selection of the letter from a number of possibilities).
- Conditional Entropy H(X∣Y) Initially we don't know what the value of H(X∣Y) is.
- Mutual Information (I(X;Y)) Initially the mutual information between X and Y is unknown.
After Asking Questions (and successfully typing the letter):
- Entropy (H(X)): We still don't know the value of H(X).
- The mutual information I(X;Y) increases by 3 bits, because 3 binary questions were asked gaining 1 bit of information each. That reflects the total amount of information gained by Y that was necessary to eliminate all uncertainty about X. However, we still don't know the value of I(X;Y), we only know the delta.
- The conditional entropy H(X∣Y) is 0 bits, indicating no remaining uncertainty about X given the information obtained from Y.
The initial value of H(X∣Y) can be inferred from the necessity to ask questions (and thus gain information) until H(X∣Y)=0. If gaining 3 bits of information was necessary to eliminate all uncertainty about X (i.e., knowing which letter to type), and after this information gain, H(X∣Y)=0 bits (indicating no remaining uncertainty about X given Y), then it is reasonable to conclude that the initial value of H(X∣Y) was 3 bits. We reiterate that the reduction in H(X∣Y) is directly related to the information gain measured by I(X;Y).
Information gain is a measure of the reduction in missing information. It is frequently used in the construction of decision trees from a training dataset by evaluating the information gain of each variable and selecting the variable that maximizes the information gain, which in turn minimizes missing information and divides the dataset into the most effective groups for classification. Information gain is calculated by comparing the missing information of a dataset before and after a transformation[3].
The process we've described suggests that the total amount of information needed and gained to resolve the uncertainty was equal to the initial conditional entropy. Counting the number of questions asked allows us to make the concept of conditional entropy H(X∣Y) concrete and measurable.
Knowledge Discovered calculation for the longest English word
Let's explain how to measure conditional entropy H(X∣Y) for the whole word “Honorificabilitudinitatibus” from the exercise presented here. At the end of the exercise we have the word “Honorificabilitudinitatibus” typed and along with it a sequence of zeros and ones:
0 0 1 1 1 1 1 0 1 1 1 1 1 1 1 0 0 1 1 1 0 1 1 1 0 0 1 1 0 0 1 1 1 1 1 1 1
In this sequence:- A "1" indicates an interval where the person knew what letter to type next, implying no additional information from the external source (Z) was needed at that moment. This suggests that their existing knowledge (Y) at that point was sufficient to make a decision about X (the letter to type).
- A "0" indicates an interval where the person did not know what letter to type and had to query Z to obtain the necessary information. Each "0" represents a binary question asked to Z, which directly reduces the uncertainty about X by one bit of information, contributing to the conditional entropy H(X∣Y).
To measure the conditional entropy H(X∣Y) for typing the entire word:
- Count the "0"s: Each "0" in the sequence represents a binary question asked, which corresponds to a bit of information needed to resolve uncertainty about the next letter to type. Counting the number of "0"s gives us the total number of binary questions asked throughout the process of typing the word.
- Calculate H(X∣Y): The total number of "0"s (binary questions asked) quantifies the total conditional entropy H(X∣Y) for the word. This is because the conditional entropy represents the remaining uncertainty about X (each letter to be typed) given the existing knowledge (Y) before each decision is made. The process of asking questions and receiving answers effectively reduces this uncertainty.
The sequence contains 10 instances of "0". This implies that 10 binary questions were needed to resolve the uncertainty about what letters to type for the entire word. Therefore, the total conditional entropy H(X∣Y) for typing the word, given the existing knowledge (Y) and the process of querying Z, is 10 bits.
Calculating the Information per Symbol
Given that it took 10 bits of information to type 27 symbols (letters of the word), dividing the total bits of information by the number of symbols gives the average information per symbol for the typing process.
This means, on average, each symbol in the word required about 0.37 bits of information to resolve the uncertainty about what letter to type next, given the existing knowledge and the process of querying an external source Z.
This calculation is based on the total conditional entropy H(X|Y) = 10 bits needed to type all 27 letters of the word, where the conditional entropy represents the total uncertainty resolved or information gained through the process of asking questions.
This metric provides insight into the efficiency of the knowledge acquisition process in this specific scenario. It indicates how much information, on average, was needed per letter to type the entire word, reflecting the average reduction in uncertainty or the average information gain per symbol, given the initial knowledge state Y and the assistance from querying Z.
Importantly, this calculation of information per symbol specifically reflects the conditional entropy H(X|Y) aspect and the process of augmenting existing knowledge Y to resolve uncertainty about the sequence X, not the mutual information between the sequence and the knowledge base per se.
How to cite:
Bakardzhiev D.V. (2022) Knowledge Discovery Process. https://docs.kedehub.io/kede/kede-knowledge-discovery-process.html
Works Cited
1. Dochy, F., Segers, M., and Buehl, M. M. (1999). The relation between assessment practices and outcomes of studies: the case of research on prior knowledge. Rev. Educ. Res. 69, 145–186. doi: 10.3102/00346543069002145
2. Schmidt HK, Rothgangel M, Grube D. Prior knowledge in recalling arguments in bioethical dilemmas. Front Psychol. 2015 Sep 8;6:1292. doi: 10.3389/fpsyg.2015.01292. PMID: 26441702; PMCID: PMC4562264.
3. Quinlan, J.R. Induction of decision trees. Mach Learn 1, 81–106 (1986). https://doi.org/10.1007/BF00116251
Getting started


