What is Knowledge
Distinction between data, information and knowledge
Distinction between data, information and knowledge
Data represents the quantifiable aspects of the world around us, devoid of context or meaning. Information emerges as this data is processed, organized, and analyzed. Yet, it is knowledge, the culmination of this process, that equips individuals with insights and understanding to make informed decisions. This hierarchical flow from data to information to knowledge is the cornerstone of informed decision-making, enabling us to assess the effectiveness of interventions with precision and clarity.
The essence of knowledge, as explored by thinkers like Dretske and echoed by Davenport and Prusak, lies not in its tangible form but in its possession by the human mind.
Dretske describes information as ‘that commodity capable of yielding knowledge, and what information a signal carries is what we can learn from it. Knowledge is identified with information-produced (or sustained) belief, but the information a person receives is relative to what he or she already knows about the possibilities at the source[6] .
Davenport and Prusak give the following description: “Knowledge derives from information as information derives from data. If information is to become knowledge, humans must do virtually all the work”[7].
Boisot's insights further illuminate this dynamic: "Knowledge builds on information that is extracted from data. Data may or may not convey information to an agent. Whether it does so or not depends on an agent’s prior stock of knowledge. Thus whereas data can be characterized as a property of things, knowledge is a property of agents predisposing them to act in particular circumstances. Information is that subset of the data residing in things that activate an agent – it is filtered from the data by the agent’s perceptual or conceptual apparatus. Information, in effect, establishes a relationship between things and agents. Knowledge either consolidates or undergoes modifications with the arrival of new information. In contrast to information, knowledge cannot be directly observed. Its existence can only be inferred from the action of agents.”[8]
Tuomi challenges traditional hierarchies and argues that the hierarchy from data to knowledge is actually inverse; knowledge must exist before information can be formulated and before data can be measured to form information. His central argument is that knowledge does not exist outside of an agent (a knower)[9].
This inversion emphasizes the foundational role of the knower in shaping what is measured and known, a notion that resonates with the idea that information is converted to knowledge once it is processed in the mind of individuals and knowledge becomes information once it is articulated and presented in the form of text, graphics, words, or other symbolic forms[10].
We define information as "answers without the questions", The answers might be stored in a book, a video, DNA, source code etc.
We define knowledge as the combination of questions and their answers, while information is just the answers without the questions. In this view, knowledge represents the context and the meaning behind the answers, whereas information is the raw data or facts themselves. Information is a necessary ingredient for knowledge, but knowledge is more than just the sum of the information that it contains. This distinction, can help to understand that knowledge is always embedded in some context or questions, and that is what gives it value, while information alone is valueless, because it has no meaning, context or questions in regard of. It is also worth noting that while knowledge represents the understanding of certain facts, it can also be used to generate new questions and thus information, which can lead to further growth of knowledge.
We define "missing information" as "questions without answers," in contrast to the definition of "knowledge" as "questions and their answers." This distinction highlights the idea that knowledge is complete, having both questions and answers, while missing information refers to the gaps in knowledge, the things that are unknown or not yet understood. This distinction also corresponds to the idea that knowledge is an accumulation of information, and that every new question that is answered contributes to this accumulation, and any question that hasn't been answered yet, represents missing information.
We define "ignorance" as "no questions and no answers" as the opposite of the definition of "knowledge" as "questions and their answers." In this context, "ignorance" refers to a lack of curiosity or interest in a particular subject or topic, and a lack of awareness or understanding of it. It is the state of being uninformed and unaware, having no questions to ask and no answers to seek. While "knowledge" refers to an accumulation of information that results from asking questions and seeking answers, ignorance refers to a lack of motivation or capability to do so. However, "ignorance" shouldn't be viewed as a negative thing, it is just a state of not having knowledge about a particular subject or thing. And also, one can still have knowledge about a variety of things and still be ignorant about some other things.
| Name | Questions | Answers |
|---|---|---|
|
Ignorance |
No |
No |
|
Information |
No |
Yes |
|
Missing information |
Yes |
No |
|
Knowledge |
Yes |
Yes |
In order to understand what knowledge is, let's refer to the game of hiding a gold coin.
The game of hiding a coin
In order to better show the difference between knowledge and information let's consider the following game.
Suppose we have eight boxes as shown below. There is a coin hidden in one of the boxes.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
 |
In order to find the coin we are allowed to ask binary questions i.e. questions with “Yes” or “No” answers. The boxes are with equal size hence there is a probability of 1/8 of finding the coin in any specific box.
There are many ways we can decide what binary questions to ask. Here are two extreme and well-defined strategies.
| Brute force strategy | Optimal strategy |
|---|---|
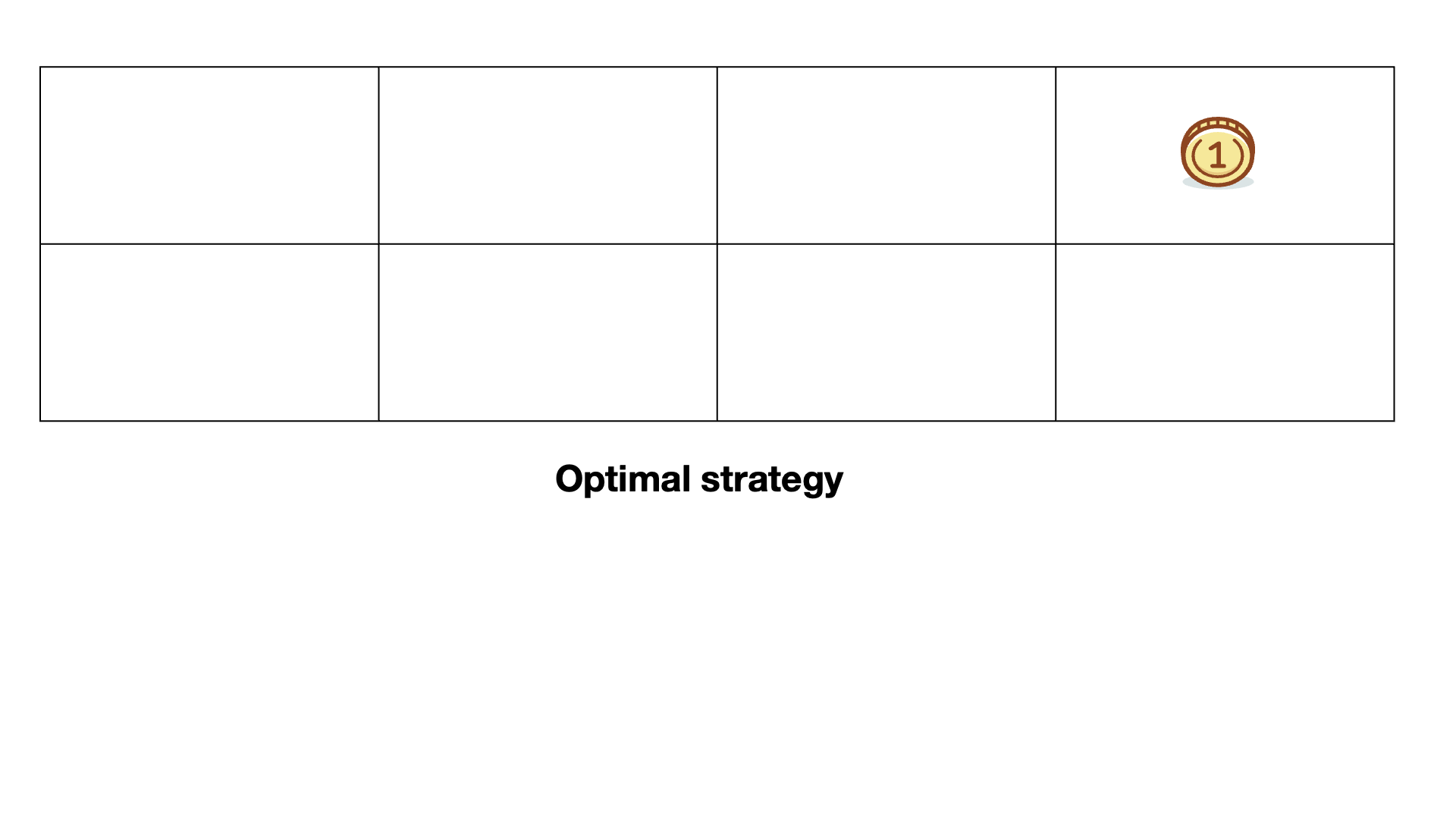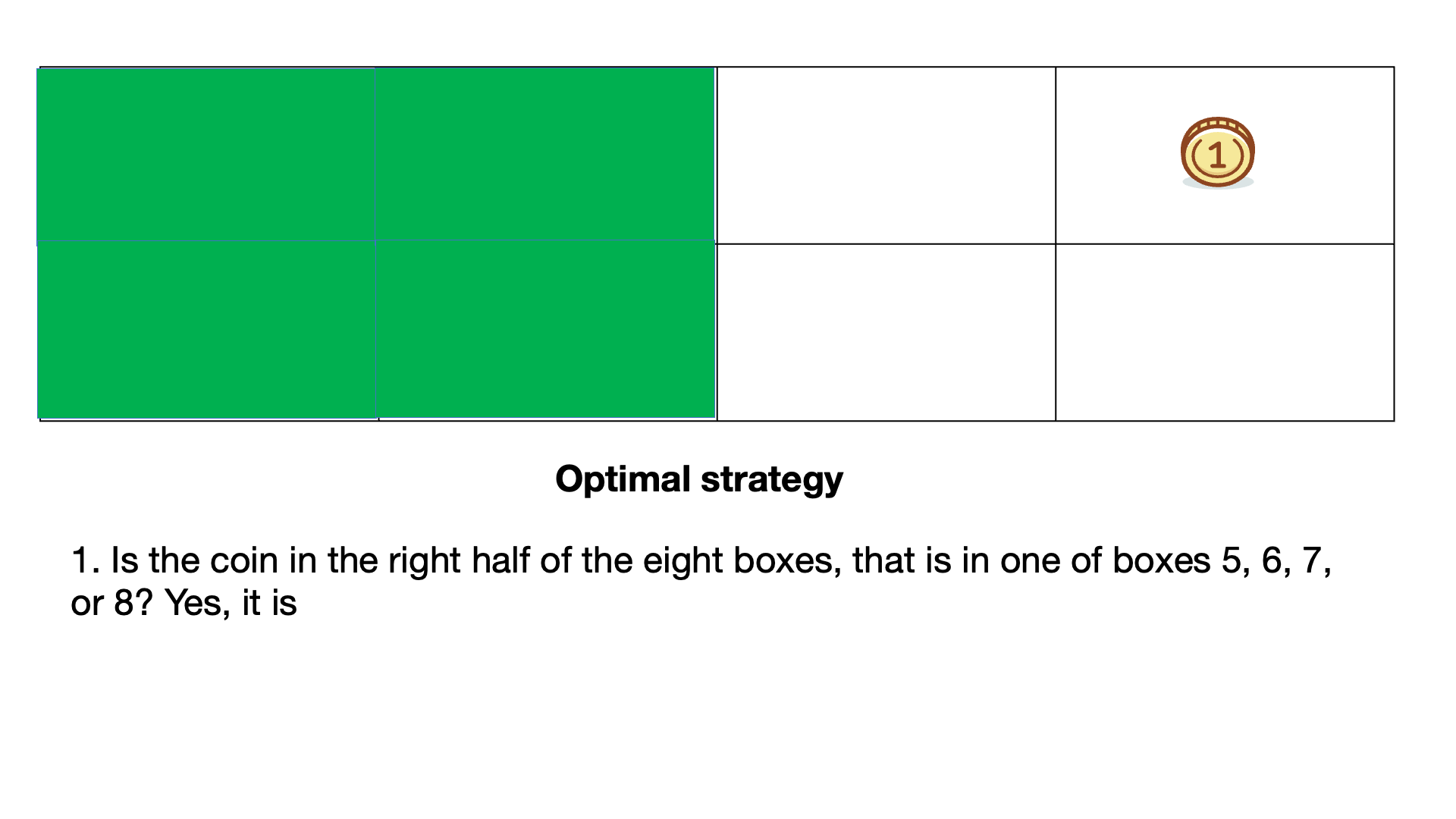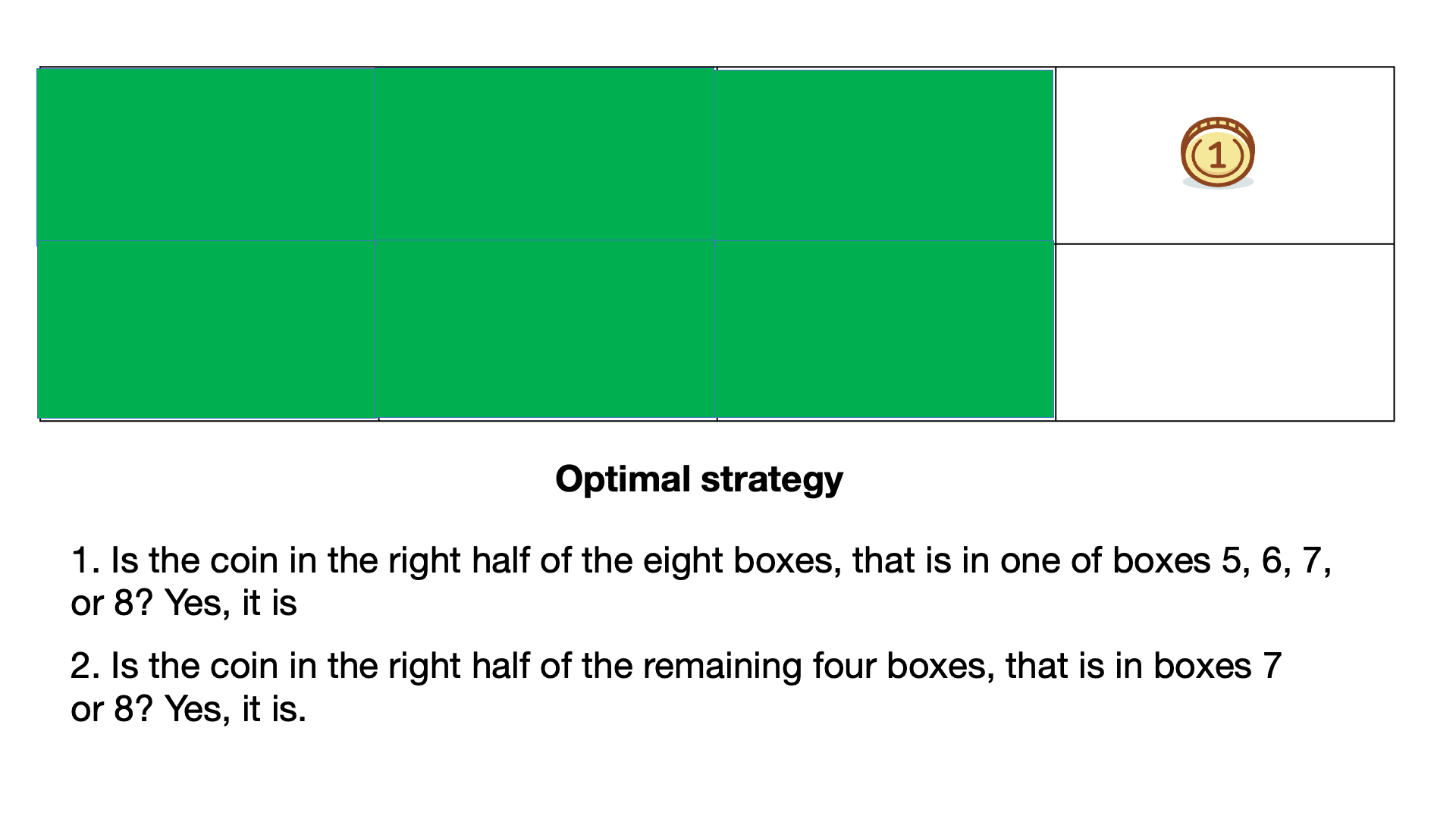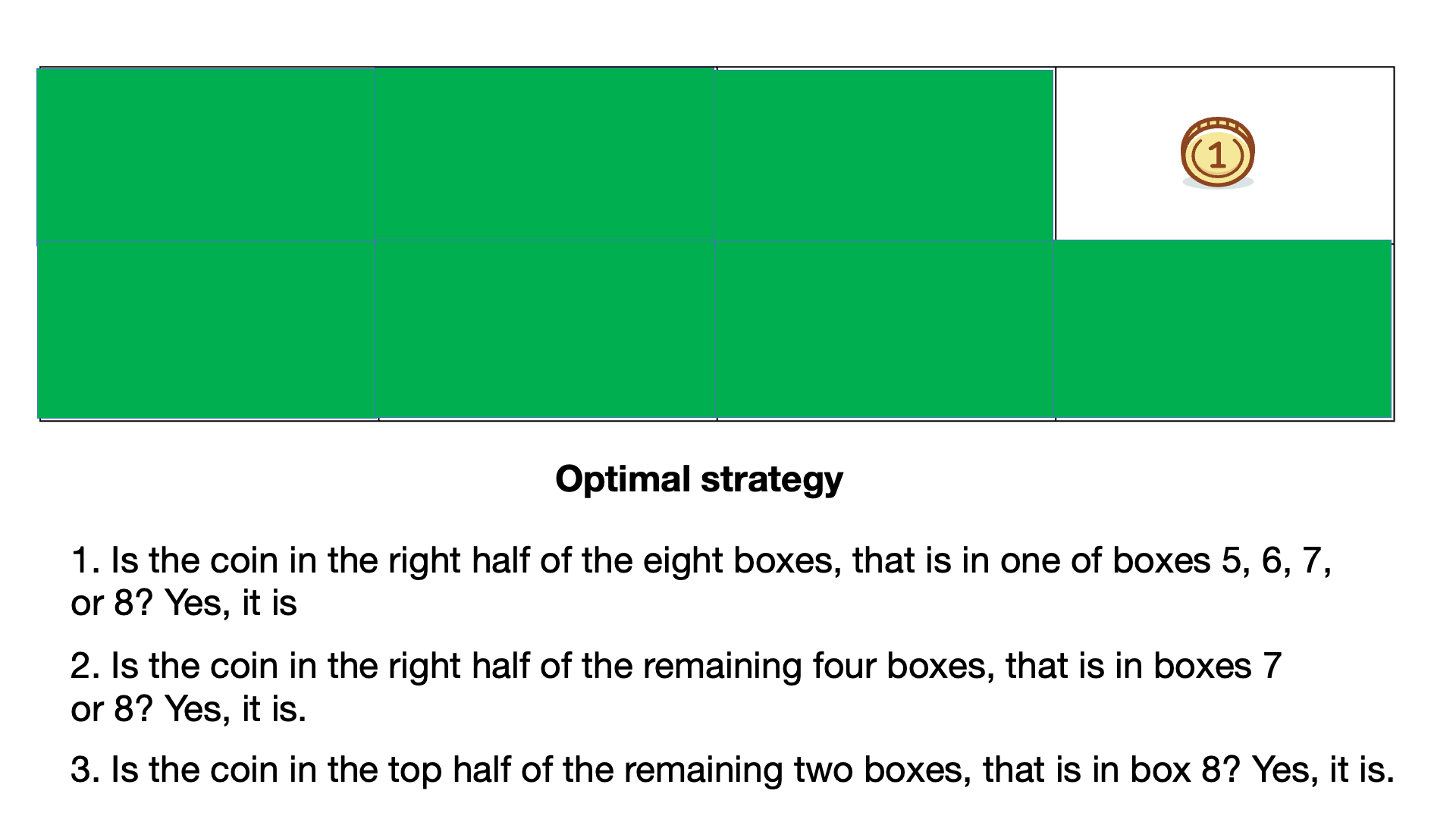
| 1) Is the coin in box 1? No, it isn't. | 1) Is the coin in the right half of the eight boxes, that is in one of boxes 5, 6, 7, or 8? Yes, it is. |
| 2) Is the coin in box 2? No, it isn't. | 2) Is the coin in the right half of the remaining four boxes, that is in boxes 7 or 8? Yes, it is. |
| 3) Is the coin in box 3? No, it isn't. | 3) Is the coin in the right half of the remaining two boxes, that is in box 8? Yes, it is. |
| 4) Is the coin in box 4? No, it isn't. |
|
| 5) Is the coin in box 5? No, it isn't. |
|
| 6) Is the coin in box 6? No, it isn't. |
|
| 7) Is the coin in box 7? No, it isn't. |
|
Below is an animated example of Brute force strategy when we search for a gold coin hidden in 1 of 8 boxes.

When using the brute force strategy with the first question we remove 1/8 of the possible coin locations. With the second question we remove 1/7 of the remaining possible coin locations. With the seventh question we remove 1/2 or 50% of the remaining possible coin locations.
Below is an animated example of Optimal strategy when we search for a gold coin hidden in 1 of 8 boxes.
Using the optimal strategy with each question asked we remove 1/2 or 50% of the possible coin locations.
Applying the brute force we have a small 1/8 probability of finding the coin with one question but we may need to answer up to seven questions. With the optimal strategy we need to ask exactly three questions. If we compare the two strategies we see that we need to ask at least one question and at most seven questions. The average number is three questions.
Shannon, in his Communication Theory of Secrecy Systems, showed that when selecting 1 from N options using only yes/no responses, the most efficient method is successive dichotomies—first dividing options into groups rather than checking items one by one[24]. This approach is vastly faster, especially as N grows.
Many investigations were carried out on the way children play the popular “20-questions” game to find out the required information with the minimal number of questions. The results are that the first-graders (aged about 6) almost always chose the “brute force strategy.” From the third-graders (aged about 8), only about one third used “brute force strategy” and the rest used a kind of "optimal strategy." Of the sixth-graders (aged about 11), almost all used a kind of "optimal strategy." Clearly the young children leap hurriedly to ask specific questions, hoping to be instantly successful. We see that at quite an early age, children intuitively feel that certain strategies of asking questions are more efficient than others; that is, efficient in the sense of asking the minimum number of questions to obtain the required information. The older children invest in thinking and planning before asking[2].
Missing information
"Information is not knowledge. Let's not confuse the two.” ~ W. Edwards Deming
Now we are ready for definitions from the information theory.
In using the term information in information theory, one must keep in mind that it is not the value of the information itself, nor the amount of information carried by a message,that we are concerned with, but the length of the message that carries the information.
“Missing information” is defined by the Information Theory introduced by Claude Shannon[1].

We can express the amount of missing information H in terms of the distribution of probabilities. In this example, the distribution is: {1/8, 1/8, 1/8, 1/8, 1/8, 1/8, 1/8, 1/8} because we have 8 boxes with equal sizes.
For calculating H we use Shannon's formula[1]:
where n is the number of boxes, p is the probability to find the coin in each box
The amount of missing information H in a given distribution of probabilities (p1, p2,...pn) is an objective quantity. H is independent of the strategy we choose of asking questions i.e. to acquire it. In other words, the same amount of information is there to be obtained regardless of the way or the number of questions we use to acquire it.
H only depends on the number of boxes and their size. The larger the number of boxes, the larger the average number of questions we need to ask in order to find the coin. The choice of strategy allows us to acquire the same amount of information by less or more than the average number of questions. The optimal strategy guarantees that we will get all the missing information by the average number of questions.
We gain missing information by asking binary questions. If an answer to a binary question allows us to exclude some of the possible locations of the coin then we say that we acquired some “missing information”. If the question allows us to exclude 50% of the possible locations we say that we acquired 1 bit of information.
Self-information
In information theory, the information content, self-information, surprisal, or Shannon information is a basic quantity derived from the probability of a particular event occurring from a random variable.
Any object or event y that has a probability p(X = x) carries a quantity of information equal to
that quantifies the number of questions with A possible answers that we would need to ask to determine y. The logarithm's base, A, could have any value, but we will always assume that A = 2 and therefore that information is measured in "bits", i.e. in binary questions.
The formula -logP(X = x) is a representation of self-information, which quantifies the amount of information obtained when one learns an event y from the random variable Y has occurred, and is equal to the negative logarithm of the probability of X.
The formula is derived based on the principle that the amount of information or surprise you gain from an event is inversely proportional to its probability. The less probable the event, the more "surprising" it is, and thus the more information it provides.
The Shannon entropy of a random variable is the expected value of the self-information of all possible outcomes of that random variable, according to the probability distribution of the variable
For instance, if we're dealing with a decimal digit, which can take one of 10 different values (0 to 9) with equal probability, then the self-information of a single event (in this case, a particular decimal digit chosen uniformly at random from 0 to 9) is given by -log2(p), where p is the probability of that specific outcome. Since each of the 10 digits are equally likely in a uniform distribution, p = 1/10 for each digit, so the self-information for a particular digit is -log2(1/10) = log2(10) = 3.322 bits. This can be interpreted as the average number of binary yes/no questions you would need to ask to guess a random decimal digit.
The Shannon entropy, which is the average (expected) self-information over all possible events, also happens to equal 3.322 bits in this case, since all digits are equally likely. However, in a non-uniform distribution, where some digits are more likely than others, the entropy would be less than the self-information of the least likely digit.
The anthropomorphic nature of missing information
"Even at the purely phenomenological level, entropy is an anthropomorphic concept. For it is a property, not of the physical system, but of the particular experiments you or I choose to perform on it." ~ Edwin Jaynes [5]
While Jaynes' statement originally pertained to thermodynamics entropy, it also applies to missing information, as the two are closely related[5].
In order to understand what knowledge is, let's refer to the game of hiding a gold coin. If I know that the coin is in the right half of the eight boxes while you do not know where it is, I have less missing information on the location of the coin than you have. If I know the exact box where the coin is while you do not know where it is, I have zero missing information on the location of the coin than you have. Notice the word "know". This knowledge is clearly subjective — you're missing more information than me.
Both experimental and theoretical definitions lead to the conclusion that missing information is an anthropomorphic concept - not in the sense that it is somehow non-physical, but rather because it is determined by the particular set of variables, parameters, and degrees of freedom defining an experiment or observation. We can always introduce as many new degrees of freedom as we like[5].
Once we recognize the anthropomorphic nature of missing information, it is easier to understand the next logical observation: that for each physical system, there corresponds an infinite number of information systems, defined once again by the variables we choose to use and monitor.
Thus, missing information is technically infinite, but made finite only by the finiteness of our measurement device (experiment, observation, interview) used to query the system.
Knowledge
"All knowledge is in response to a question. If there were no question, there would be no scientific knowledge." ~ Gaston Bachelard, The Formation of the Scientific Mind
Different perspectives on knowledge exist among scholars and practitioners. Frequently, knowledge has been perceived as an object, defined as “justified true belief”. It is assumed that knowledge can be codified and separated from the minds of people. The idea extends beyond human cognition to include mechanized, documented, and automated forms of knowledge, broadening the scope of knowledge carriers. Some authors argue that knowledge can also be embedded in entities other than human beings[11][12]. They also identify:
- mechanized knowledge - where the knowledge necessary to carry out a specific task has been incorporated in the hardware of the machine,
- documented knowledge - where knowledge has been stored in the form of archives, books, documents, ledgers, instructions, charts, design specifications etc. and
- automated knowledge - where knowledge has been stored electronically and can be accessed by computer programs that support specific tasks.
The importance of information embedded in documented routines and technologies is acknowledged to be important in the process of knowing and doing. For example, technologies might yield knowledge with reverse engineering. However, documented mechanized and automated knowledge are considered as information in this research, rather than knowledge, following the definition of [11].
A second perspective on knowledge stresses that knowledge could only reside in the mind of people and can be defined as “that which is known”, i.e. knowledge being embedded in individuals[13]. Only people can ‘know’ and convert ‘knowing’ into action, and it is the act of thinking that can transform information into knowledge and create new knowledge[14].
Although the first two perspectives on knowledge still guide many practitioners and academics, a third perspective is gaining ground. This perspective defines knowledge as “the social practice of knowing”, addressing the social character of knowledge[15]. Knowledge is considered to be embedded in a community rather than just in one individual. It suggests knowledge to supersede any one individual and to be highly context dependent[16][17][18][19]
Knowledge may be viewed from five other perspectives (1) a state of mind, (2) an object, (3) a process, (4) a condition of having access to information, or (5) a capability[11].
In line with defining knowledge as ‘justified belief that increases an entity’s capacity for effective action’[20][21][22], in here knowledge is defined as: “collective understanding plus the ability to transform this understanding into actions, which yields performance being dependent of the situation in which it is learned and used”[23]
Prior knowledge
The term "prior knowledge" generally refers to all the knowledge and abilities a person has acquired before encountering a new learning experience. This includes factual information, concepts, principles, procedures, as well as more tacit forms of knowledge such as skills and competencies.
Here's a detailed breakdown:
- Factual Knowledge: This includes facts, concepts, and information that a person has learned, for example, the knowledge of programming languages in computer science.
- Procedural Knowledge: This involves knowing how to do something. For instance, knowing the steps involved in solving a mathematical problem or coding a software program.
- Conceptual Knowledge: This involves understanding principles and theories, for example, understanding the laws of physics or the principles of object-oriented programming.
- Metacognitive Knowledge: This involves understanding one's own thought processes and having strategies for learning, problem-solving, and decision-making.
- Skills: T These are abilities to perform certain tasks. For instance, a skill might be being able to write proficiently, to communicate effectively, or to use a particular software tool.
- Competencies: These involve a combination of knowledge, skills, and attitudes required to perform a task effectively. For example, project management competency would involve knowledge about project management methodologies, skills in using project management tools, and attitudes such as leadership and teamwork.
- Experience: This includes the insights, understanding, and tacit knowledge gained from personal and professional experiences.
- Attitudes and Beliefs: These include personal values, attitudes towards learning, self-efficacy beliefs, and motivation, which can influence how a person approaches new learning situations.
- Cultural Knowledge: This includes understanding of cultural norms, practices, and values, which can influence how a person interprets and responds to new information or situations.
It's important to note that all these elements interact and influence each other. For example, a person's experiences can shape their skills, attitudes, and beliefs, which in turn can influence how they use and apply their factual, procedural, and conceptual knowledge. Understanding this complexity is key to understanding how prior knowledge influences learning.
in some contexts, there can be a distinction made between knowledge and skills:
- Knowledge usually refers to theoretical understanding or factual information that a person has learned. For instance, a person might have knowledge of programming concepts or business strategies.
- Skills and Competencies, on the other hand, are more about the practical ability to perform tasks or actions. Skills are usually developed through practice. For example, being able to write code, manage a project, or negotiate a deal are skills.
Although there can be a conceptual distinction between knowledge (knowing what or why) and skills (knowing how), in practice, the two are closely linked and often overlap. A person's prior knowledge base typically includes both their theoretical or factual knowledge and their practical skills and competencies.
For example, if someone is learning how to code in a new programming language, their prior knowledge might include:
- Factual knowledge about the principles of programming
- Procedural knowledge about how to write code in other languages
- Skills such as problem-solving and logical thinking
- Competencies such as the ability to learn new technologies quickly
Experience is a key part of prior knowledge. Prior knowledge is constructed not only through formal education and learning processes but also through our experiences in various contexts. Experience, in this sense, refers to the insights and understandings that we develop through our direct participation in events and activities. This can include professional experience, life experiences, cultural experiences, and so forth. These experiences can shape our perspectives, influence how we approach new information or situations, and contribute to our stock of tacit knowledge—knowledge we have but may not be explicitly aware of or able to articulate. For example, a software developer's prior knowledge would include not just their formal education in computer science and their understanding of programming languages, but also their experience working on different projects, dealing with bugs, collaborating with different teams, and so forth.
The term "prior knowledge" emphasizes the temporal aspect of knowledge. This is often emphasized because it strongly influences how a person processes and integrates new information. While "existing knowledge" can be used and understood in an academic context, it is somewhat more general and could refer to the current state of knowledge in a field or a learner's knowledge at any point in time, not necessarily before a specific learning experience.
Measuring prior knowledge in bits
It's challenging to measure prior knowledge in its entirety in bits. The reason is that prior knowledge includes much more than just quantifiable information or facts. It also encompasses skills, competencies, experiences, attitudes, and beliefs, which are difficult, if not impossible, to measure in bits.
For example, how would one quantify in bits an individual's understanding of a complex theory, their problem-solving ability, or their experience working on a project? Similarly, it's hard to quantify attitudes, beliefs, or tacit knowledge (knowledge we have but may not be consciously aware of or able to articulate).
Furthermore, even if we focus just on factual knowledge, the bit is a unit of information that expresses the amount of uncertainty that is resolved by knowing the answer to a yes-or-no question. However, not all pieces of knowledge are equivalent or can be easily reduced to binary choices. Some pieces of knowledge might be more complex, interconnected, or nuanced than others, and this complexity is not captured when measuring knowledge in bits.
In practical terms, prior knowledge is usually assessed using a variety of methods, such as pre-tests, interviews, surveys, or reviews of past work or qualifications. These assessments aim to get a broad understanding of a person's knowledge, skills, experiences, attitudes, and beliefs, rather than trying to reduce this complex construct to a single numeric value.
True and observed missing information
In information theory, when you acquire new information about a probability distribution, it reduces the uncertainty of the distribution for you, but it does not change the actual distribution itself.
For example, the probability distribution of the game of hiding a gold coin has 3 bits of missing information. If you acquire 1 bit of that missing information, then for you, the distribution now has 2 bits of missing information, but for someone else who is not aware of the information you have acquired, the distribution still has 3 bits of missing information. This difference in the perception of the missing information is referred to as the "observed missing information" versus the "true missing information" in information theory.
Observed missing information is a measure of the missing information that is perceived by an observer given the information that the observer has acquired. The conditional missing information H(X|Y) can be seen as a measure of the "observed entropy" of X, given the value of Y, as it represents the remaining missing information in X, after taking into account the information that is known from Y. It gives us an idea of how much the knowledge of Y helps to understand X. So, if an observer has acquired some information about a distribution and the observed entropy is 2 bits, it means that the observer is aware of some information about the distribution, but there are still 2 bits of missing information that the observer is not aware of.
This information that the observer is aware of can be referred to as "prior knowledge", as it represents the understanding and awareness that the observer has about the distribution before engaging in a task to acquire all of the missing information.
The "true missing information" of a probability distribution is the amount of missing information it has when all possible information is considered. True missing information is not subjective, it is an objective measure of missing information for a certain distribution or problem, but it's not possible to measure it in practice, it's just a theoretical concept.
True missing information represents the total unconditional missing information H(X) in a random variable X, regardless of any other information that might be available. It's a measure of the best possible understanding of the information in X.
The "observed missing information" is the amount of missing information that is still present to an observer that has acquired new information. For the new person that is not aware of the information you have acquired, the observed missing information is equal to the true missing information. For you the observed missing information is 2 bits because that's the amount of missing information you perceive after you acquired new information, while the true missing information remains 3 bits, as the missing information for the distribution from a general point of view.
"Observed missing information" is subjective because it depends on the observer's prior knowledge, understanding and perspective. Thus, the amount of missing information that is perceived by the individual will be different from that of another individual who has a different set of information. It can also change with the acquisition of new information.
However, that kind of subjective missing information is not the subject matter of information theory. To define the true missing information, we have to formulate the problem as follows: “Given that a coin is hidden in one of the M boxes, how many questions does a person need to ask to be able to find out where the coin is?”
In this formulation, the true missing information is built-in in the problem. It is as objective as the given number of boxes, and it is indifferent to the person who hid the coin in the box.
It is not entirely correct to say that "prior knowledge" is the difference between "true missing information" and "observed missing information". The difference between "true missing information" and "observed missing information" is their mutual information. It quantifies the amount of information that they have in common, how much information is shared between them, but it doesn't necessarily reflect the level of understanding or the level of awareness of an observer.
Knowledge is subjective and conditional
"There is no neutral observation. The world doesn't tell us what is relevant. Instead, it responds to questions. When looking and observing, we are usually directed toward something, toward answering specific questions or satisfying some curiosities or problems." ~ Teppo Felin
Individuals receive information about something by asking questions. This way they may or may not reduce their observed missing information. At least they have a chance to reduce it. If the observed missing information of a distribution is 0 bits, it means that there is no remaining missing information in X, given the information they have. It means that the observer has a complete understanding of the distribution.
It's important to note that the observed missing information is a subjective evaluation of actual missing information. The same distribution could have different observed missing information for different observers depending on their prior knowledge, understanding and perspective they have.
Additionally, true missing information is a theoretical concept that represents the best possible understanding of a certain distribution, and it's usually impossible to achieve it in practice. It could be that even if your "observed missing information" is 0 bits, there might still be some missing information that you are not aware of, so even if you have complete knowledge from your perspective, it might not be the case from a theoretical perspective.
So, if your observed missing information of distribution is 0 bits, it means that you are not aware of any missing information in the distribution, and you have complete knowledge of the distribution given certain assumptions, but it doesn't mean that you have a complete understanding of the distribution without considering any other information. You might know everything about the distribution given certain assumptions, but other information that is not taken into account could still be missing.
The assumptions among other things include the specific questions you've had. The questions you choose to ask shape the way you think about a problem or a distribution, and they can influence the kind of information you gather and the way you interpret it. The questions you ask can reveal patterns, relationships, and connections that you would not have noticed otherwise, and they can help you understand and make sense of the information you have.
If you add new specific questions the observed missing information may change.
Tailoring Descriptions to the Listener's Knowledge
The length and detail of a description depend on the listener's prior knowledge, context, and needs. If someone is already familiar with the subject, concise references or technical terms might suffice. However, when addressing someone less familiar, the description should include more background or definitions to bridge their knowledge gap.
Effective communication also considers the purpose and context—what the listener needs to know to achieve understanding. Striking a balance is crucial: too much detail can overwhelm, while too little can confuse. This principle reflects the knowledge-centric approach to communication, where adapting to the listener’s needs ensures clarity and efficiency.
The various Interpretations of the quantity H
The value H has the same mathematical form as the entropy in statistical mechanics. Shannon referred to the quantity H he was seeking to define as “choice,” “uncertainty,” “information” and “entropy.”[1] The first three terms have an intuitive meaning.
The term "choice" is commonly understood to refer to the number of alternative options available to a person. In the context of the game, we have to choose between n boxes to find the gold coin. When n = 1 we only have one box to choose from and therefore have zero choice. As n increases, the amount of choice we have also increases. However, the "choice" interpretation of H becomes less straightforward when considering unequal probabilities. For example, if the probabilities of eight boxes are 9/10, 1/10, 0, . . . , 0, it is clear that we have less choice than in the case of a uniform distribution. However, in the general case of unequal probabilities, the “choice” interpretation of H H not satisfactory. Therefore, we will not use the “choice” interpretation of H[3].
The meaning of H as the amount of uncertainty is derived from the meaning of probability. We can say that H measures the average uncertainty that is removed once we know the outcome of a random variab;e.
The “missing information” interpretation of H is intuitively appealing since it is equal to the average number of questions we need to ask in order to acquire the missing information[3]. If we are asked to find out where the coin is hidden, it is clear that we lack information on “where the coin is hidden.” It is also clear that if n=1 i.e we know where the coin is, we need no information. As n increases, so does the amount of the information we lack, or the missing information. This interpretation can be easily extended to the case of unequal probabilities. Clearly, any non-uniformity in the distribution only increases our information, or decreases the missing information. All the properties of H listed by Shannon are consistent with the interpretation of H as the amount of missing information. For this reason, we will use the interpretation of H as the amount of missing information.
The basic idea of information as number of questions
The relation between the Missing Information and the number of questions is the most meaningful interpretation of the quantity H. By asking questions, we acquire information. The larger the Missing Information, the larger the average number of questions to be asked. There is a mathematical proof that the minimum average (expected) number of binary questions required to determine an outcome of a random variable X lies between H(X) and H(X) + 1[4].
The amount of missing information in a given distribution (p1, . . . , pn) is independent of the strategy, or of the number of questions we ask. In other words, at the end of questioning the same amount of missing information is obtained regardless of the way or the number of questions one asks to acquire it.
The same missing information H can come from different search spaces each with a different number of states N. On the other hand, totally different information H might come from search spaces each with the same number of states N. It all depends on the probability of occurrence of each of the N states in a search space. In general, the below inequality holds for any random variable with N outcomes:

The equality holds when each state has the same probability of occurring. For example we are given the 26 letters (27 if we include the space between words) from the English alphabet. The frequency of occurrence of each of these 27 letters is different and known. The total missing information for this distribution is 4.138 bits. This means that in the “best strategy,” we need to ask, on average, 4.138 questions. However, for the English language, log2(N) = log2(27) = 4.755. In this case the equality doesn't hold because the letters are with a different probability of occurrence.
In general, when we have n equally sized boxes the average number of questions needed to find the coin location is:
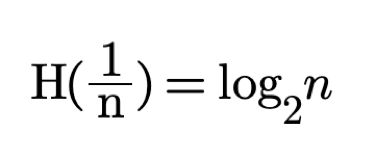
In our case because we have 8 equally sized boxes then n = 8 and H is:
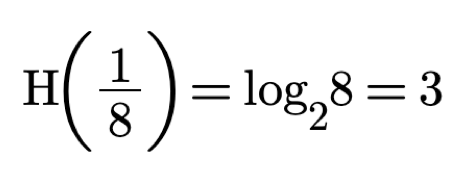
Which is what we indeed achieved using the optimal strategy.
In the case of 16 boxes H is:
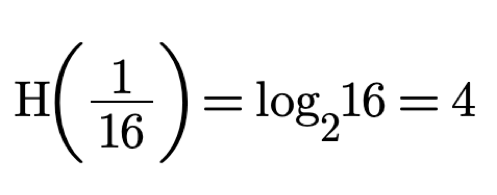
And for 32 boxes H is:
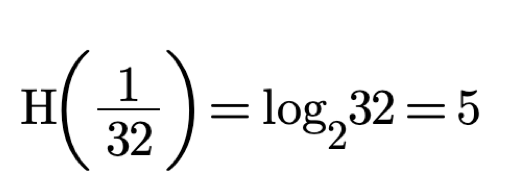
So far we looked at the case of even number of equally sized boxes. This gives an upper limit on the number of questions. When the number of boxes is odd or the boxes are not equally sized we can only reduce the number of questions necessary to obtain the missing information. For example below we have a coin hidden in three unequally sized boxes where box #3 is twice as big as #1 and #2.
| 1 | 2 | 3 |
|---|---|---|
| 1/4 | 1/4 | 1/2 |
The probabilities of the boxes are 1/4, 1,4, 1/2. In this case H is:
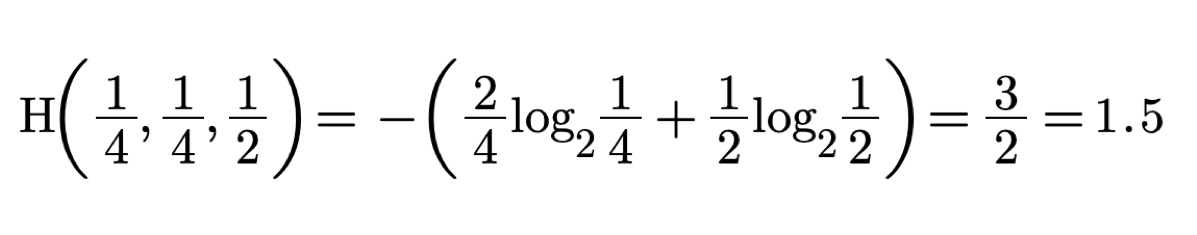
The value of H is 1.5 because if the coin is in box #3 and we ask is it in box #3 thus excluding 50% of the possible locations we will find the coin with only one question. But if the coin is in box #1 and with each question we exclude 50% of the possible locations we will have to ask two questions. That's why the average number of questions is (1+2)/2=1.5
What is one bit of information?
In the case of 2 boxes we will need to ask only one question. The value of the missing information H in this case is one. as calculated below:
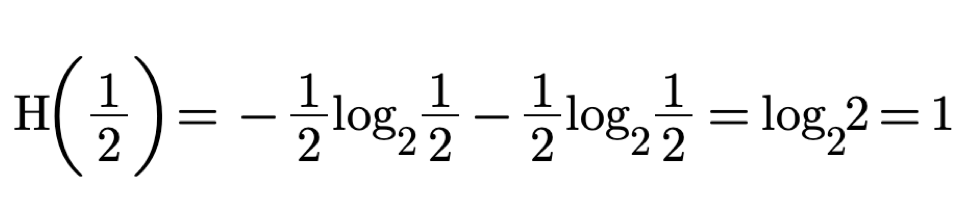
With p equals 1/2 we acquire exactly 1 bit of information.
This bit can be represented by one binary digit. Hence, many people confuse one bit of information with a binary digit. However bits are not binary digits. The word bit is derived from binary digit, but a bit and a binary digit are fundamentally different types of quantities. A binary digit is the value of a binary variable, whereas a bit is an amount of information. To mistake a binary digit for a bit is a category error analogous to mistaking a one litre bottle for a litre of water. Just as a one litre bottle can contain between zero and one litre of water, so a binary digit (when averaged over both of its possible states) can convey between zero and one bit of information.
Uncertainty and precision
Shannon initially used “uncertainty” for his “missing information” measure. Uncertainty is the opposite of precision. If uncertainty is reduced by one bit, then increased by one bit i.e. precision is doubled because half of the uncertainty is gone (half of possible values are gone).
For example, an observer initially believes a distance is between 4 and 6 m. If after an observation (measurement) the observer believes it to be between 4.5 and 5.5 m, then the observation has halved the range of uncertainty about the length in question. That is because the initial uncertainty was U=6-4=2m, and after the observation was U = 5.5-4.5 = 1 m. Since half of the possible values of the uncertainty were removed then the observation has provided one bit of information about the thing measured.
Works Cited
1. Shannon CE. (1948), A Mathematical Theory of Communication. Bell System Technical Journal. ;27(3):379-423. doi:10.1002/j.1538-7305.1948.tb01338.x
2. Ben-Naim, A.,(2012), Discover Entropy and the Second Law of Thermodynamics: a Playful Way of Discovering a Law of Nature, World Scientific, Singapore, Singapore
3. Ben-Naim, A. (2008), A Farewell to Entropy: Statistical Thermodynamics Based on Information, World Scientific Publishing, Singapore
4, Cover, T. M. and Thomas, J. A. (1991), Elements of Information Theory, John Wiley and Sons, New York. page.95 in 5.7 SOME COMMENTS ON HUFFMAN CODES
5. Jaynes ET. 1965 Gibbs vs. Boltzmann entropies. Am. J. Phys. 33, 391–398. (doi:10.1119/ 1.1971557)
6, Dretske, F. (1981). Knowledge and the flow of information. MIT Press
7. Davenport, T. H. and Prusak, L. (1998). Working knowledge : how organizations manage what they know. Harvard Business School Press
8. Boisot, M. H. (1998). Knowledge assets; Securing competitive advantage in the information economy. Oxford University Press.
9. Tuomi, I. (1999). Data is more than knowledge: implications of the reversed hierarchy for knowledge management and organizational memory. 32nd Hawaii International Conference on System Sciences. Los Alamitos.
10. Alavi, M. and Leidner, D. E. (2001). Review: knowledge management and knowledge management systems: conceptual foundations and research issues. MIS Quarterly 25, 107-136.
11. Boersma, S. K. T. and Stegwee, R. A. (1996). Exploring the issues in knowledge management. Information technology management and organizational innovations. Washington D.C.
12. Spek, R. v. d. and Spijkervet, A. (1997). Knowledge management; dealing intelligently with knowledge. CIBIT.
13. Polanyi, M. (1998). Personal Knowledge: Towards a Post-Critical Philosophy. Routledge.
14. McDermott, R. (1999). Why information technology inspired but cannot deliver knowledge management. California Management Review 41, 103-117.
15. Blackler, F. (1995). Knowledge, knowledge work and organizations: an overview and interpretation. Organization Studies 16, 1021-1046.
16. Brown, J. S. and Duguid, P. (1991). Organizational learning and communities of practice. Organizational Science 2, 40-57.
17. Lave, J. and Wenger, E. (1991). Situated learning: legitimate peripheral participation. Cambridge University Press.
18. Wenger, E. (1998). Communities of practice; learning, meaning and identity. Cambridge University Press.
19. Orr, J. (1996). Talking about machines: an ethnography of a modern job. Cornell University Press.
20. Nonaka, I. (1994). A dynamic theory of organizational knowledge creation. Organization Science 5, 14-37
21. Nonaka, I. and Takeuchi, H. (1995). The knowledge-creating company: how Japanese companies create the dynamics of innovation. Oxford University Press
22. Huber, G. P. (1991). Organizational learning: the contribution process and the literatures. Organization Science 2, 88-115.
23. Boer, N.. (2005). Knowledge Sharing within Organizations.
24. Shannon, C. E. Communication theory of secrecy systems. Bell System technical Journal, 28, 656-715, 1949
Getting started


