Applying the Theory of Constraints (ToC) in software development
A ToC solution for knowledge work
Related Articles
The Five Focusing Steps
The Theory of Constraints (TOC) was developed by Dr. Eliyahu M. Goldratt in the late 20th century. TOC focuses on the idea that a production system's overall performance is limited by its weakest link or constraint, and that only identifying and improving this constraint can lead to significant improvements in the entire system. TOC is based on several principles, including the importance of ongoing improvement, the use of critical metrics to manage the system, and a focus on the flow of work through the production process. It has been applied in manufacturing, supply chain management, project management, and other fields, and has been used as a framework for problem-solving and decision-making.
The Five Focusing Steps of the Theory of Constraints (TOC) are:
- Identify the Constraint: Determine which resource or process in the system is the limiting factor, or constraint, and focus on improving it.
- Exploit the Constraint: Use the constraint to its fullest potential to maximize its efficiency and productivity.
- Subordinate Everything Else to the Constraint: Ensure that all other processes are aligned with and support the constraint, rather than disrupting its performance.
- Elevate the Constraint: Improve the constraint's capacity and performance to increase the overall system's performance.
- Repeat: Continuously identify and work on the next constraint in the system until all constraints have been addressed. The focus then shifts back to the first step to ensure that the system remains optimized.
Knowledge is a property of the system
"Any improvement not made at the constraint is an illusion.”~ Eliyahu M. Goldratt [1]
When we start a software development project the best is to establish an iterative process for managing the project constraint which, as we do know, is the knowledge discovery process. The goal is deliberately reducing our missing information and increasing our knowledge.
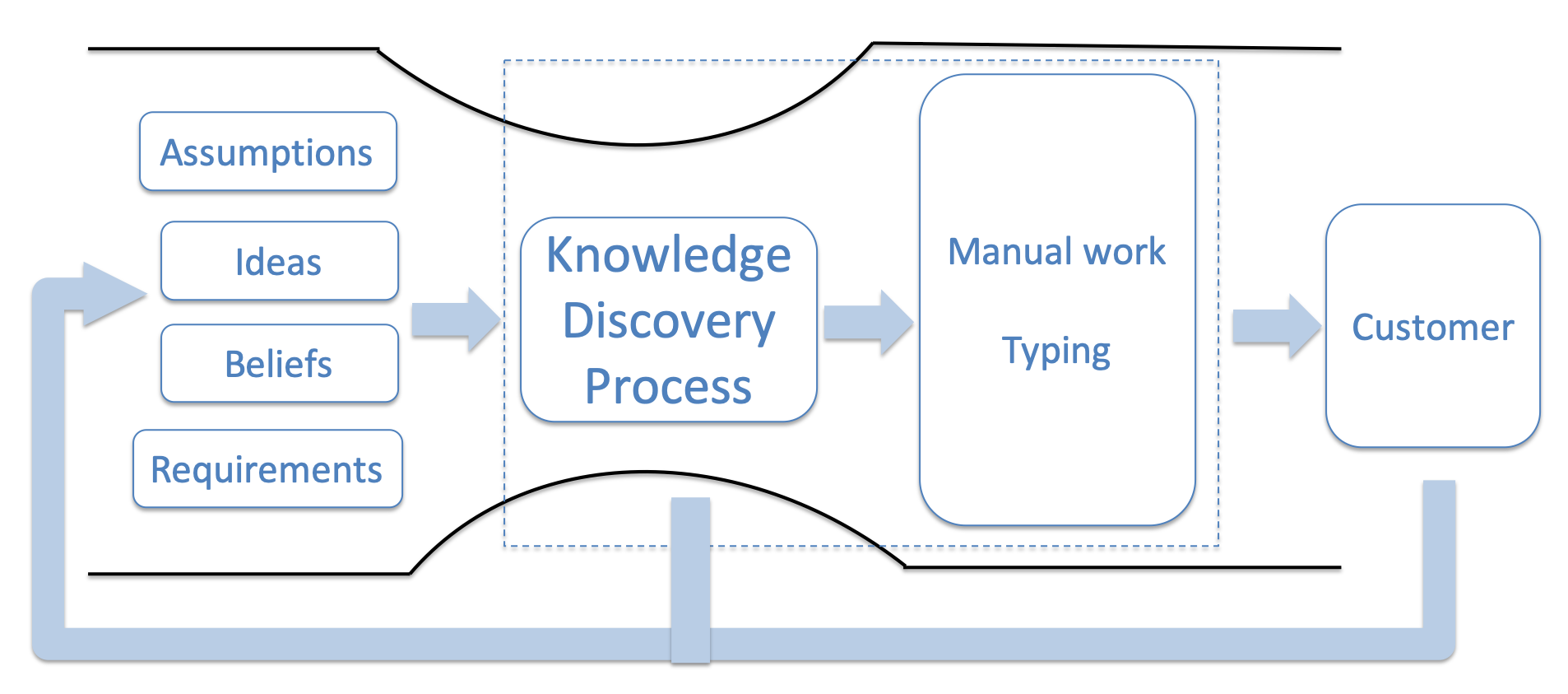
From a knowledge perspective, the constraint is not a person - a senior developer or another specialist. For example, let's say on a project there are two senior and two junior developers. Since the juniors will most probably ask the seniors questions the available work time for the seniors will be effectively reduced. One may think that makes the senior the system constraint, but they will be wrong. The seniors need to provide answers i.e. increase the knowledge of juniors exactly because the juniors don't have enough knowledge in the form of experience and intuition. Here is an example.
Knowledge is a property of the system the knowledge worker operates in. It includes the knowledge of the developer, but also the knowledge of her teammates, the Product Owner, the documentation available, the applicable knowledge in StackOverflow etc.
In software development the system constraint can be measured by the missing information (measured in bits) the developers can acquire per unit time.
Let's consider an example scenario, where we have 3 work items A, B, C. They will be implemented by a team of software developers. Work item A has 50 bits of missing information, item B has 2 bits of missing information, item C has 4 bits of missing information. Here's how the Five Focusing Steps of the Theory of Constraints could be applied to this scenario:
- Identify the Constraint: In this case, the constraint is the missing information the developers can acquire per hour. To determine this, the amount of missing information for each work item (A, B, and C) is assessed.
- Exploit the Constraint: The developers should work on the work item with the largest amount of missing information, which in this case is item A (50 bits). By doing this, the developers will be able to reduce their uncertainty most efficiently.
- Subordinate Everything Else to the Constraint: The team should prioritize work item A and allocate efforts accordingly, while ensuring that the other work items do not interfere with the acquisition of the missing information for item A.
- Elevate the Constraint: The team should work to increase the speed at which the missing information can be acquired. This could be done by improving processes, tools, or training for the developers.
- Repeat: The cycle of focusing on the constraint, exploiting it, subordinating everything else to it, and elevating it should be repeated until all work items have been delivered.
In real life, there are no single values. Thus, most likely item A doesn't have exactly 50 bits of missing information, but some random number between 5 and 50 bits of missing information. The missing information for item A follows some probability distribution.
In this case, the constraint is still the missing information the developers can acquire per hour, but this time it will depend on the random number of missing information for work item A. An analysis or simulation may be performed to determine the average or most likely value of bits of missing information for work item A, and the other work items can be compared against this. Based on the analysis, the team should prioritize work on the work item with the largest amount of missing information. If work item A has the largest missing information, then the developers should focus on it first. Here a practical approach for doing that is presented.
Logic for prioritization
According to Shannon's theory, information and uncertainty are two sides of the same coin: the more uncertainty there is, the more information we gain by removing the uncertainty
The reasoning behind the logic for prioritizing the work item with the highest uncertainty ( largest missing information) can also be explained using the Information Theory by Claude Shannon. According to this theory, information is a measure of the reduction of uncertainty in a system. The more information that is acquired, the less uncertain the system becomes.
The missing information of the system measures the uncertainty in the system and can be reduced by acquiring new information that narrows down the possible states of the system.
By continuously acquiring new information and updating the missing information of the system, we can apply the Five focusing steps by selecting the work item with the largest missing information (i.e., the work item that reduces the uncertainty the most).
In the example scenario of work items A, B, and C, each work item has a certain amount of missing information. The developers aim to acquire the missing information to reduce the uncertainty in the system and increase their knowledge. The rate at which the developers can acquire missing information is the limiting factor of the system and can be considered as the channel capacity
Shannon's theory states that the channel capacity can be maximized by sending the most important information first, where the importance of information is determined by its missing information (a measure of the uncertainty in the information).
The reasoning can be explained by viewing the rate at which the developers can acquire missing information as the channel capacity and prioritizing the work item with the largest amount of missing information to maximize the channel capacity and acquire the missing information most efficiently.
In the scenario where work item A has the largest missing information, the developers should focus on work item A first. By asking one binary (Yes/No) question about work item A, they can remove half of the possibilities and reduce the missing information of the system. By doing so, the developers can acquire the most information in the shortest amount of time, as they are able to reduce the uncertainty in the system most efficiently. So, in this example scenario, the developers should prioritize work item A over work item B and work item C, as they can remove the most possibilities and reduce the missing information of the system most efficiently. The math behind this is presented in Appendix A.
Additional questions to consider
We have the following questions to consider regarding the application of TOC to knowledge work:
- How will the Five focusing steps be applied if the missing information for all work items is not known with certainty?
- How will the Five focusing steps be applied if there are additional work items in the system with varying amounts of missing information?
- How will the Five focusing steps be applied if the missing information for work items changes over time?
- What metrics will the developers use to measure the progress of reducing the missing information of the system?
- How can the information rate be used in forecasting when the work will be completed?
How will the Five focusing steps be applied if the missing information for all work items is not known with certainty?
Knowledge is subjective and conditional, as explained in details here.
One way to handle uncertainty in the amount of missing information for work items is presented here. In this way, the Five focusing steps can be applied even when the missing information for some work items is not known with certainty.
How will the Five focusing steps be applied if there are additional work items in the system with varying amounts of missing information?
In the presence of multiple work items with varying amounts of missing information, we can extend the approach used to the entire system. The missing information of the system can be calculated using the formula from Appendix A.
By using the missing information, we can identify the work item with the highest uncertainty and prioritize it in accordance with the second focusing step of TOC. We can then repeat this process iteratively, reducing the missing information of the system one work item at a time until all work items have been addressed.
In this way, the Five focusing steps can be applied to a system with multiple work items with varying amounts of missing information by using it as a measure of the uncertainty in the system and reducing the total missing information one work item at a time.
How will the Five focusing steps be applied if the missing information for work items changes over time?
In a scenario where the missing information for work items changes over time, we need to continuously evaluate and update the missing information of the system. The missing information of a system is a measure of the uncertainty in the system and can change as new information is acquired.
One approach is to use an algorithm that updates the missing information of the system after each iteration, where each iteration corresponds to acquiring additional information about one of the work items. The algorithm computes the missing information of the system after acquiring information about each work item and selects the work item that reduces the missing information the most.
In this way, the Five focusing steps can be applied to a scenario where the missing information for work items changes over time by continuously updating the missing information of the system and reducing the missing information one work item at a time.
The reduction in missing information can be quantified using the formula from Appendix A.
What metrics will the developers use to measure the progress of reducing the missing information of the system?
The developers can use metrics from Information Theory to measure the progress of reducing the missing information of the system. One of the key metrics is the reduction in missing information (ΔH) as a result of acquiring new information.
The missing information of the system can be calculated using the formula from Appendix A.
Another metric that can be used to measure the progress of reducing the missing information of the system is the information rate (R), which measures the amount of information acquired per unit of time.
The information rate can be calculated using the formula from Appendix A.
By continuously monitoring these metrics, the developers can measure the progress of reducing the missing information of the system and make decisions on which work item to focus on next to maximize the reduction in missing information.
How can the information rate be used in forecasting when the work will be completed?
The information rate (R) can be used in forecasting when the work will be completed. By continuously monitoring the information rate, the developers can estimate the amount of missing information that will be acquired per unit of time. This information can be used to estimate the total time required to acquire all the missing information for a work item.
For example, let's say the information rate is 10 bits per hour, and work item A has a missing information of 50 bits. The estimated time required to complete work item A can be calculated as: T = 50 bits / 10 bits/hour = 5 hours
Similarly, the estimated time required to complete work items B and C can be calculated based on their respective missing information and the information rate.
It's important to note that this estimate may not be exact because the missing information may change over time as new information is discovered and the information rate may also vary. However, monitoring the information rate and continuously updating the estimate can help the developers make a more accurate forecast of when the work on items will be completed.
How does the reduction in missing information due to the Five focusing steps impact the overall performance of the software development team?
The reduction in missing information due to the Five focusing steps can positively impact the overall performance of the software development team by reducing uncertainty and increasing the efficiency of the team's work.
The missing information of a system can be seen as a measure of the information required to describe the state of the system. By reducing the missing information of the system through the Five focusing steps, we can reduce the amount of information required to describe the state of the system, which in turn reduces the uncertainty in the system.
In the context of software development, this reduction in uncertainty can lead to more efficient and effective problem-solving, as the team has a clearer understanding of the state of the system.
The reduction in missing information can be quantified using the formula from Appendix A.
A larger reduction in missing information (ΔH) corresponds to a greater reduction in uncertainty and a higher impact on the overall performance of the software development team.
Appendix A
The missing information of a system can be defined (assuming i.i.d.) as the sum of the missing information of all the work items:
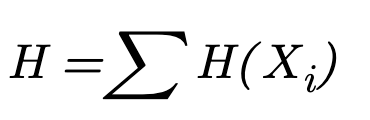
The reasoning of prioritizing the work item with the largest amount of missing information can be presented using math formulas from the Information Theory: Let H be the total missing information of the system, and HA, HB, and HC be the missing information of work items A, B, and C, respectively.
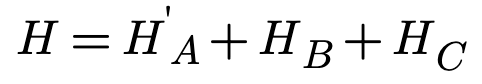
By asking one binary (Yes/No) question about work item A, the developers can reduce the number of possibilities for work item A by half. By reducing the missing information of work item A, the developers can reduce the total missing information of the system and acquire more information in the shortest amount of time by prioritize work item A over work item B and work item C
Acquiring the most information in the shortest amount of time can be explained using the concept of Shanon information rate, It is defined as the amount of information received per unit of time.
The information rate can be calculated using the following formula:
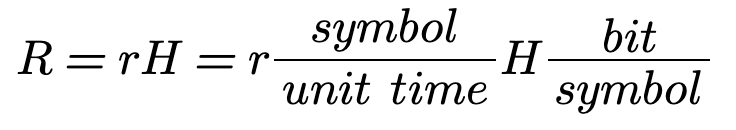
Or simply as:
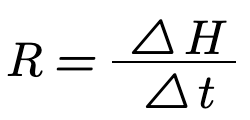
The reduction in missing information (ΔH) can be calculated using the following formula:

References
1. Goldratt, E. M. (2012). The Goal: A Process of Ongoing Improvement - 30th Anniversary Edition (3rd edition). North River Press.
How to cite:
Bakardzhiev D.V. (2022) Using Theory of Constraints (ToC) in software development. https://docs.kedehub.io/kede-improvements/kede-toc.html
Getting started


