Knowledge Discovery Efficiency (KEDE) and Ashby's Law of Requisite Variety

Abstract

Real-world applications of Ashby’s Law face three key challenges: (i) Combinatorial explosion—enumerating all system and environmental states becomes intractable, especially with hidden variables; (ii) Dual control dilemma—regulators must both amplify internal variety and attenuate external variety, a difficult balance in complex, multiscale systems; and (iii) Resource constraints—limited data, computation, and organizational capacity hinder implementation. Existing solutions reduce but do not resolve these issues.

We address this impasse by adopting Ashby’s strict black-box perspective: only external behaviour is observable. First we define the multi-staged selection process of narrowing down and selecting the appropriate response from the set of alternative responses as the Knowledge Discovery Process. We then label H(X|Y) as the knowledge to be discovered, which is the gap in internal variety that had to be compensated by selection. This quantifies how much disorder the regulator still permits and, conversely, how close the system comes to meeting Ashby’s requisite-variety condition. In information-theoretic terms, perfect regulation requires H(X|Y) = 0. Then we quantify quantify the knowledge to be discovered H(X|Y) based on the observable outcomes E. Building on this result, we generalize Knowledge-Discovery Efficiency (KEDE) - scalar metric that quantifies how efficiently a system closes the gap between the variety demanded by its environment and the variety embodied in its prior knowledge. KEDE operationalises requisite variety when internal mechanisms remain opaque, offering a diagnostic tool for evaluating whether biological, artificial, or organisational systems absorb environmental complexity at a rate sufficient for effective regulation. Finally we present applications of KEDE in diverse domains, including typing the longest English word, measuring software development, testing intelligence, basketball game, assembling furniture, and speed of light in medium.

1. Introduction

The Law of Requisite Variety, formulated by W. Ross Ashby, states that for a system to effectively regulate its environment, it must have at least as much variety/complexity as its environment. This principle is foundational in disciplines such as cybernetics, control theory, and machine learning.

The concept of requisite variety has since been applied across diverse domains, including organizational theory, ecology, and information systems. It underscores the necessity for systems to adapt to environmental complexity in order to maintain stability and achieve intended outcomes.

Real-world attempts to apply Ashby’s Law of Requisite Variety face three persistent obstacles. (i) Combinatorial explosion: enumerating all relevant states of a system and its environment quickly becomes intractable, especially when hidden or unmeasured variables are present. (ii) Dual control dilemma: a regulator must simultaneously amplify its own control variety and attenuate external variety—an optimization that is delicate in multiscale, hierarchical, and time-varying settings such as digital ecosystems or military command structures. (iii) Resource constraints: limited data, computational power, and organisational capacity often preclude sophisticated control architectures. Existing remedies—markup-language state catalogues, iterative multidimensional sampling, and distributed self-organising controllers—mitigate but do not eliminate these limitations.

In section 2, we provide a detailed overview of Ashby's Law of Requisite Variety, including its mathematical formulation and implications for system regulation. We also discuss the present day understanding of residual variety and its significance in the context of Ashby's Law. In section 3, we discuss the challenges of applying Ashby's Law to real-world systems, including combinatorial explosion, dual control dilemma, and resource constraints. We propose a solution to these challenges by treating the system as a black box, observing probability of successful outcomes to disturbances, and estimate the gap in its internal variety based on that. In section 4, we start establishing the solution by introducing the Knowledge Discovery Process, which is narrowing down and selecting the appropriate response from its set of alternative responses. We then label H(X|Y) as the knowledge to be discovered, which is the gap in internal variety that had to be compensated by selection. In section 5, we show how to quantify the knowledge to be discovered H(X|Y) based on the observable outcomes E. In section 6, we generalize the Knowledge-Discovery Efficiency (KEDE) - scalar metric that quantifies how efficiently a system closes the gap between the variety demanded by its environment and the variety embodied in its prior knowledge. Finally, in section 7, we explore applications of KEDE in various domains, demonstrating its utility as a diagnostic tool for evaluating system performance and adaptability.

2. The Law of Requisite Variety

In practice, the question of regulation usually arises in this way: The essential variables E are given, and also given is the set of states S in which they must be maintained if the organism is to survive (or the industrial plant to run satisfactorily). These two must be given before all else. Before any regulation can be undertaken or even discussed, we must know what is important and what is wanted. ... It is assumed that outside considerations have already determined what is to be the goal, i.e. what are the acceptable states S. Our concern...is solely with the problem of how to achieve the goal in spite of disturbances and difficulties[1].

Given a set of elements, its variety is the number of elements that can be distinguished. Thus the set {g b c g g c } has a variety of 3 letters. Variety comprises any attribute of a system capable of multiple 'states' that can be made different or changed.

The Law of Requisite Variety, formulated by W. Ross Ashby states that:

For a system to effectively regulate its environment, it must have at least as much variety as its environment

Ashby's Law is held true across the diverse disciplines of informatics, system design, cybernetics, communications systems and information systems.

Mathematical Formulation

In Ashby’s terms, we can think of the system as a transducer:

D \overset{R}{\Rightarrow} T \overset{}{\Rightarrow} E

Where:

D be the set of disturbances, representing the possible states of disturbances that a system may experience.
R be the set of responses, representing the possible regulatory actions that counteract disturbances.
T be the set of outputs, representing the final state of the system after regulation.
E be the set of outcomes or essential variables, representing the desired states or outputs that the system aims to achieve. E may be as simple as the 2-element set {good, bad}, and is commonly an ordered set, representing the preferences of the organism. Some subset of E can be defined as the “goal”[8].

This can be represented as a Table of Outcomes (T) where:

Rows represent disturbances D
Columns represent regulatory responses R
Entries represent outputs T

T		R
T		r₁	r₂	r₃	...
D	d₁	t₁₁	t₁₂	t₁₃	...
	d₂	t₂₁	t₂₂	t₂₃	...
	d₃	t₃₁	t₃₂	t₃₃	...
	d₄	t₄₁	t₄₂	t₄₃	...
	...	...	...	...	...

Each input from D is transformed via selection into a response $r \in R$ , which is then processed to produce an output $t \in T$ . which results in an outcome $e \in E$ , which is the essential variable that the system aims to achieve. There is a one-to-one mapping between variables T and E, so that V(T) is equal to V(E).

If R does nothing, i.e. keeps to one value, then the variety in D threatens to go through T to E, contrary to what is wanted. It may happen that T, without change by R, will block some of the variety and occasionally this blocking may give sufficient constancy at E. More commonly, a further suppression at E is necessary; it can be achieved only by further variety at R.

Ashby's Law can be expressed mathematically as the smallest variety that can be achieved in the set of actual outcomes cannot be less than the quotient of the number of rows divided by the number of columns. $V (E) \geq \frac{V (D)}{V (R)}$

Where:

V(D) = variety in the disturbances
V(R) = variety in the regulatory responses
V(E) = variety in the outcome (essential variables)

This inequality shows that the variety in the outcomes cannot be reduced below the division between the variety in the disturbances and the variety in the regulatory responses.

For perfect regulation, we need V(E) to be stable or close to 1 (only one outcome):

\frac{V(D)}{V(R)} \approx 1 \Rightarrow V(R) \approx V(D)

The law reflects a fundamental insight: control is about the ratio of disturbances to regulatory responses, not just their arithmetic difference.

Information-Theoretic Formulation

For many purposes the variety may more conveniently be measured by the logarithm of its value. If the logarithm is taken to base 2, the unit is the bit of information. In practice, we use the Shannon information entropy, denoted by H. For a quantifiable variable, entropy is just another measure of variance.

Applying this to Ashby’s Law we get:

\log_{2} (\frac{V (D)}{V (R)}) = \log_{2} V (D) - \log_{2} V (R) = H (D) - H (R)

Now we can express Ashby’s Law in terms of information theory as:

H (E) ​ \geq H (D) ​ - H (R ​)

For effective control: $H (R) \geq H (D)$ . If $H (R) < H (D)$ , the system lacks sufficient variety to manage disturbances, leading to instability.

Ashby’s law can thus be reformulated clearly:

The information-processing capacity (entropy) of a control system must be at least as large as the information (entropy) in the system it regulates.

It has been shown shown that the law of requisite variety can be extended to include knowledge or ignorance by simply adding this conditional uncertainty term[31]:

H (E) ​ \geq H (D) ​ + H (R | D) - H (R)

Where:

H(R) is the entropy of the regulator, representing its information-processing capacity or variety.
H(D) is the entropy of the disturbances, representing the complexity of the environment.
H(R|D) is the conditional entropy of the regulator given disturbances, representing the ignorance of the regulator about how to react correctly to each appearance of a disturbance D. Only a regulator that knows how to use available regulatory acts in an optimal way will reach the optimal result of regulation,

To achieve control, the regulator R must possess sufficient information-processing capacity (entropy) such that the following relation is achieved: $H (R) \geq H (D)$ $H (R | D) = 0$

When this holds, the regulator potentially has enough information-processing capability or variety to reduce the conditional entropy H(D∣R) to zero or close to zero. (i.e. the complexity of the environment can not exceed that of the system), which means the system fully matches the environment[7].

Since $H (R) - H (R | D) = I (D : R)$ the law simplifies to: $H (E) \geq H (D) - I (D : R)$

Without regulation, the entropy of the system is H(D). The presence of the regulator should ideally remove uncertainty from D. Thus, the difference between H(D) and H(D∣R) represents how much uncertainty the regulator removes:

I (D; R) = H (D) - H (D | R)

Here, I(D;R) is the mutual information or the channel capacity, representing how effectively the regulator R reduces uncertainty in the regulated environment D. The conditional entropy H(D|R) measures the uncertainty remaining in D after considering the actions or states of regulator R.

If H(D∣R) is large, then after the regulator has acted or observed, significant uncertainty about the controlled environment remains. This indicates poor regulation or insufficient regulator variety.
Conversely, if H(D∣R) is low (ideally approaching zero), then the regulator effectively predicts or controls the states of the regulated environment D.

To maximize control, we want to maximize mutual information.

I (D; R) = H (D)

In other words, the conditional entropy of the controlled system given the regulator should be as small as possible ideally zero - implying perfect regulation.

H (D | R) \approx 0

Today, Ashby’s Law of Requisite Variety is considered a generalization of Shannon's 10th theorem (sometimes called the "Noisy channel coding theorem") which states that communication through a channel that is corrupted by noise may be restored by adding a correction channel with a capacity equal to or larger than the noise corrupting that channel. The disturbance D, which threatens to get through to the outcome E, clearly corresponds to the noise; and the correction channel is the system R, which is supposed to restore the outcome E[8].

The law of Requisite Variety says that R 's capacity as a regulator cannot exceed R 's capacity as a channel of communication. Thus, all acts of regulation can be related to the concepts of communication theory by noticing that the “disturbances” correspond to noise, and the “goal” is a message of zero entropy, because the target value E is unchanging.

Residual Variety

In the context of Ashby’s Law of Requisite Variety, residual variety refers to the variety that the regulator fails to absorb. Information-theoretically, this can be understood in two ways:

The residual variety is the uncertainty H(D|R) about the disturbance that remains after observing the regulator's response. This represents the part of the disturbance entropy that the regulator doesn't "know about" or cannot predict i.e. the regulator's "informational blindness" to what it's trying to control. It focuses on the input side - how much the regulator doesn't know about what's hitting the system (the disturbance).
The residual variety is the uncertainty H(E) in a system's outcomes that remains in the system after regulation. It focuses on the output side - how much unpredictability persists in what we care about the essential variable.

Both interpretations are two sides of the same coin - they quantify how much unpredictability is left once the regulator has made its move. If the regulator perfectly counters every disturbance (full requisite variety), the residual variety in both forms would be zero. If not, some variety remains in the outcome due to H(R|D).

The relationship between them connects through the information-theoretic version of Ashby's law as: $H (E) \geq H (D | R)$ i.e. the uncertainty in outcomes (given the regulator’s actions) is at least the uncertainty in disturbances remaining (given those actions).

This formulation elegantly captures the fundamental cybernetic insight that effective control requires both sufficient regulatory capacity and sufficient information about what you're trying to regulate.

Now we focus on one important consideration, which is that E (essential variable) values are observable. These are the outcomes we can measure and care about - system performance, output quality, stability measures, etc. Being observable, we can empirically estimate H(E) by collecting data on how E varies given different regulator states R This makes H(E) (residual variety) a measurable quantity in practice.

H(D|R) presents observability challenges, as disturbances D may not be directly observable - they could be internal system dynamics, environmental factors we can't measure, or complex interactions we can't decompose. Even if some disturbances are observable, the full set D might include hidden or latent factors that we cannot directly measure or quantify. This makes H(D|R) potentially unobservable or only partially estimable and often theoretical or abstract.

This creates an important asymmetry in cybernetic analysis:

H(E) is observable and measurable, allowing us to empirically assess how well the regulator is performing in controlling outcomes.
H(D|R) may not be fully observable, making it difficult to quantify the regulator's knowledge of disturbances it's regulating.

This is why H(E) is often the more practically useful measure - it tells us what we can observe about system performance. That is reflected in the literature as well, where work focuses on observable outcomes rather than unobservable disturbances[29,30,35,36,37,38,39,40,41,42,43,44,45].

3. Core challenges in applying Ashby's Law to real systems

We conducted a literature review aimed at identifying the primary challenges and limitations associated with applying Ashby’s Law in real-world systems.

A central challenge that emerges is the measurement of variety. In most of the reviewed literature, the concept of variety is either poorly defined or not explicitly measured, resulting in ambiguity and potential misinterpretation of the law’s implications. Key obstacles to effective measurement include:

The direct measurement of variety is fundamentally incomputable for all but the simplest systems [14].
Hidden variables introduce uncertainty and complicate measurement efforts [15].
Trade-offs often arise between variety at different scales [16].
A combinatorial explosion occurs when attempting to enumerate all possible system states [15,16].
Resource limitations constrain the feasibility of comprehensive measurement [20].
Environmental complexity is frequently “unknowable,” preventing complete assessment [25].
Most studies lack explicit or standardized methods for quantifying variety [14,17–20,25,27].
Existing approaches often lack rigorous quantitative validation [17].

Several measurement methods have been proposed, including:

Markup language-based variety estimation [18],
Iterative sampling techniques [21],
Entropy and determinism metrics to evaluate communication complexity, where greater variety was correlated with improved effectiveness [22],
Social network and cluster analysis to assess resilience [23], and
Multiple Correspondence Analysis (MCA) for capturing organizational complexity [24].

In addition, a subset of studies estimate variety through observed performance rather than structural attributes. Notable examples include:

Communication-based performance measures, employing determinism metrics to evaluate repeatable patterns in team behavior [22];
Team performance assessments, using task-based surveys to evaluate an organization’s risk-handling capabilities [23];
Leadership behavior analysis, based on actual behavioral responses to simulated scenarios [26]; and
Relative performance comparisons, assessing organizational effectiveness across contexts using perception-based rather than absolute metrics [14].

While these performance-based approaches provide practical insights, they often rely on subjective or indirect indicators of variety, which may introduce biases and limit their generalizability. For example, performance outcomes may fail to account for hidden variables or the underlying complexity of the system [15]. Moreover, these approaches remain underrepresented in the literature, where structural and theoretical analyses still dominate.

In summary, although numerous methods for measuring variety have been proposed, no single comprehensive or universally accepted solution has emerged. Quantification remains a persistent challenge in the application of Ashby’s Law to complex real-world systems.

Solution

These challenges significantly hinder the practical application of Ashby’s Law. Whether considering a human, an AI model, or an organization, we are typically limited to observing external behavior rather than internal mechanisms—unless we are able to "open the box."

Ashby himself emphasized that all real systems can be considered black boxes. He argued that while black boxes mimic the behavior of real objects, in practice, real objects are black boxes: we have always interacted with systems whose internal workings are, to some extent, unknown.

This leads to what Ashby termed the black box identification approach [2], which involves:

Perturbing the system by applying external disturbances,
Measuring the system’s responses to these perturbations, and
Inferring the internal variety or capacity from the observed input-output relationships.

In most practical scenarios, we are only able to observe the outcomes of a system—typically, the probability that the system produces a correct response, denoted as P(E=1). These observable outcomes can be used to infer bounds on the system’s internal variety—specifically, the extent of variety it must possess or lack in order to exhibit the observed behavior.

We propose such an approach: to treat the system as a black box, observe the probability of successful outcomes to disturbances, and estimate the gap in its internal variety based on that. Let E denote the event that the system gives a correct response to disturbance D, and let R be the regulator’s action. In information-theoretic terms, perfect regulation requires H(D|R) = 0. Using our novel information-theoretic estimator, empirical estimates of P(E=1) are used to quantify H(D|R) in bits of information. This quantifies how much disorder the regulator still permits and, conversely, how close the system comes to meeting Ashby’s requisite-variety condition.

4. Knowledge Discovery Process

The process of selection may be either more or less spread out in time. In particular, it may take place in discrete stages. What is fundamental quantitatively is that the overall selection achieved cannot be more than the sum (if measured logarithmically) of the separate selections. (Selection is measured by the fall in variety.) 13/17[2]

Successful (essential) outcomes do not depend solely on the variety of responses available to a system; the system must also know which response to select for a given disturbance. Effective compensation of disturbances requires that the system possess the ability to map each disturbance to an appropriate response from its repertoire. This “system knowledge” can take various forms across different systems—for example, it may be encoded as a set of conditional rules of the form: if (perceived disturbance), then (response) [29]. The absence or incompleteness of such knowledge can be quantified using the conditional entropy H(R|D), which captures the system’s ignorance about how to respond correctly to each disturbance D[31]. In other words, H(R∣D) measures how much the system lacks the necessary knowledge to match responses to disturbances. H(R|D) = 0 represents the case of no uncertainty or complete knowledge, where the action is completely determined by the disturbance. $H (R) = H (R | D)$ represents complete ignorance. This requirement may be called the law of requisite knowledge[29]. Mathematically, requisite knowledge can be expressed as: $H (R) - H (R | D) = I (R : D)$

In the absence of such system knowledge, the system would have to select responses, until eliminating all disturbances. Thus, merely increasing the response variety H(R) is not sufficient; it must be complemented by a corresponding increase in selectivity, that is, reduction in H(R|D) i.e. increasing knowledge.

We refer to the process of narrowing down and selecting the appropriate response from its set of alternative responses as the Knowledge Discovery Process.

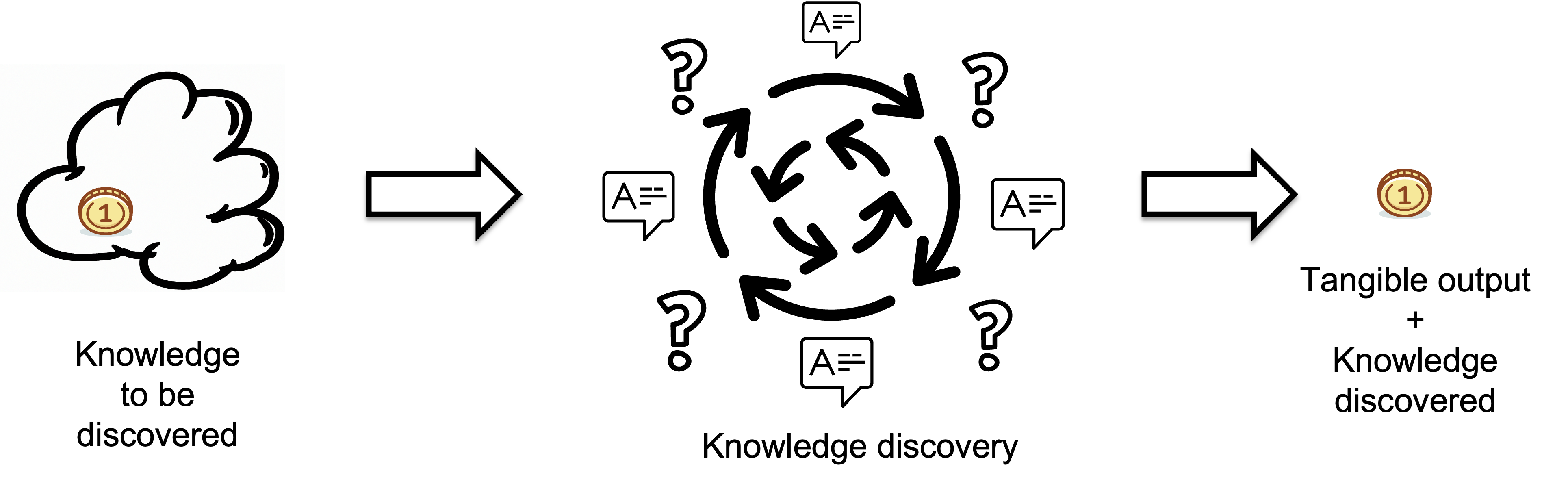
A Knowledge Discovery Process is a multi-staged selection process that transforms invisible knowledge into visible, tangible output.

Inputs represent the knowledge a regulator lacks before starting a task i.e. the missing information or knowledge that needs to be discovered, which is measured in bits. The quality of the output is assumed to meet target standards.

The Knowledge Discovery Process is a multi-stage process of selection from a range of possibilities. At each stage, the system selects the most appropriate response based on the current state of its knowledge and the disturbances it faces.

W. Ross Ashby[13/15 [2]] measures the quantity of selection in bits as:

$S = \log_{2} (\frac{V_{b e f o r e}}{V_{a f t e r}})$

Where

S is the selection (the amount by which the variety is reduced) or the information gained, i.e., how much the uncertainty has been reduced.,
V_before is the variety before the selection i.e. before a constraint (filter, decision, control action) is applied, and
V_after is the variety after the selection i.e after the constraint is applied.

Thus every time we introduce a rule or a constraint we throw away some of the possibilities and gain information equal to the logarithm of that reduction:

“How many possibilities are removed?” – that is V_before -V_after
“How many bits of information does this represent?” – that is S = log₂(V_before/V_after)

Rather than a single act, selection is often a multi-stage process of selection from a range of possibilities[2][4]. Think of it as progressively reducing uncertainty at each stage — each stage reduces the complexity for the next stage.

This staged selection process reflects how systems adapt and regulate themselves:

In adaptive systems, each stage of selection narrows possibilities and increases order.
In knowledge work, each step converts potential information into actualized, meaningful knowledge.

We can say that we've got "it from bit" - a phrase coined by John Wheeler. "It from bit" symbolizes the idea that every item in the physical world has knowledge as an immaterial source and explanation at its core[6].

We may distribute the total selection over time or over several nested feedback loops. Thus every time we introduce a rule or a constraint we throw away some of the possibilities and gain information equal to the logarithm of that reduction. Each stage can chip away part of the disturbance variety. After each stage only the surviving candidates move on to the next stage. Mathematically we have:

$V_{0} \underset{S_{1}}{\to} V_{1} \underset{S_{2}}{\to} V_{2} \underset{S_{3}}{\to} . . . \underset{S_{k}}{\to} V_{k}$

The total selection is the sum of the partial selections - because logarithms turn multiplications of ratios into additions:

$S_{t o t a l} = \sum_{i = 1}^{k} S_{i}$

Below is a “dictionary” that puts Ashby’s multi-stage selection into the language of Shannon’s conditional entropy and mutual information.

Ashby term	Symbol	Shannon term	Symbol
Initial Space of Possibilities	D	Random variable we are trying to identify	X
Total variety originally present V_before	V(D)	Entropy of X before any messages	H(X)
Constraint applied at stage i	R_i	Message/side-information revealed at that stage	Y_i
Residual Variety left after i-th selection / stage	V(D \| R₁, ..., R_<i)	Conditional entropy left at stage i	H(X \| Y_i, ..., Y_<i)
Selection (Variety reduced at stage i)	log₂(V_before/V(D \| R₁, ..., R_<i)	Mutual information gained at that stage, or the information gain	I(X;Y_i \| Y_<i)
Residual Variety left after k selections/stages V_after	V(D \| R₁, ..., R_k)	Conditional entropy after seeing all messages	H(X \| Y₁, ..., Y_k)
Total selection after k stages	log₂(V_before/V_after)	Mutual information delivered by all messages	I(X; Y₁, ..., Y_k)

Ashby’s selection in design and regulation via requisite variety are structurally identical: they describe how constraints (or regulation) reduce the variety of possible outcomes from an initial space.

Ashby’s staged selection process is the sequential acquisition of mutual information. The formula

$H (X | Y) = H (X) - I (X : Y)$

is the textbook statement, in Shannon’s symbols, of Ashby’s core idea: uncertainty that remains is the difference between the initial uncertainty and the information gained (mutual information).

When mapping one stage of selection with one filter Y we have:

Before the filter:: H(X) bits of uncertainty.
After hearing Y=y: only those x’s compatible with that value survive; the average remaining uncertainty is H(X∣Y).

The selection Ashby counts in bits is exactly the mutual information:

$S = \log_{2} (\frac{V_{b e f o r e}}{V_{a f t e r}}) = H (X) - H (X | Y) = I (X : Y)$

Shannon’s chain rule for mutual information is:

$I (X : Y_{1}, . . . . . Y_{k}) = \underset{s t a g e 1}{I (X : Y_{1})} + \underset{s t a g e 2}{I (X : Y_{2} | Y_{1})} + . . . \underset{s t a g e k}{I (X : Y_{k} | Y_{< k})}$

Those k summands are exactly the k numbers Ashby would add up when he says “the total selection is the sum of the separate selections.” So the arithmetic of staged selection is nothing more than Shannon’s chain rule written in bits.

After k filters we have:

$H (X | Y_{1}, . . . . . Y_{k}) = \underset{i n i t i a l v a r i e t y}{\underset{⏟}{H (X)}} - \underset{t o t a l s e l e c t i o n}{\underset{⏟}{[\underset{s t a g e 1}{I (X : Y_{1})} + . . . \underset{s t a g e k}{+ I (X : Y_{k} | Y_{< k})}]}}$

The principle is independent of how the ruling is expressed; all that matters is the fraction of the search-space that each stage discards. But whatever mix we choose, the grand total must still cover H(X) if we want the controlled variable to reach (or stay at) zero entropy with respect to its goal.

Ashby’s Law of Requisite Variety states, for a staged selection process is:

$H (X | Y_{1}, . . . . . Y_{k}) = 0$ $I (X : Y_{1}, . . . . . Y_{k}) = H (X)$

That is Ashby’s “requisite variety” restated: the sum of the bits removed by selection by every stage must at least equal the bits of uncertainty injected by the original range of possibilities (or by disturbances, in the regulation case).

Defining Knowledge to be Discovered

The knowledge to be discovered is the gap in internal variety that had to be compensated by selection.

Given that H(E) is called "residual variety" (the variety that remains uncontrolled in outcomes), we elect to use the term "Knowledge to be Discovered" for H(X|Y) - the gap in internal variety that had to be compensated by selection.

Thus, the variety of the disturbances, is defined as the "required knowledge" or total unconditional missing information H(X), The regulators variety, or "prior knowledge" is defined as the mutual information I(X:Y), which equals the "requisite knowledge" we discussed earlier. The "knowledge to be discovered" is the conditional information H(X|Y) - what the regulator lacks about the task before starting it i.e. the gap in internal variety that had to be compensated by selection.

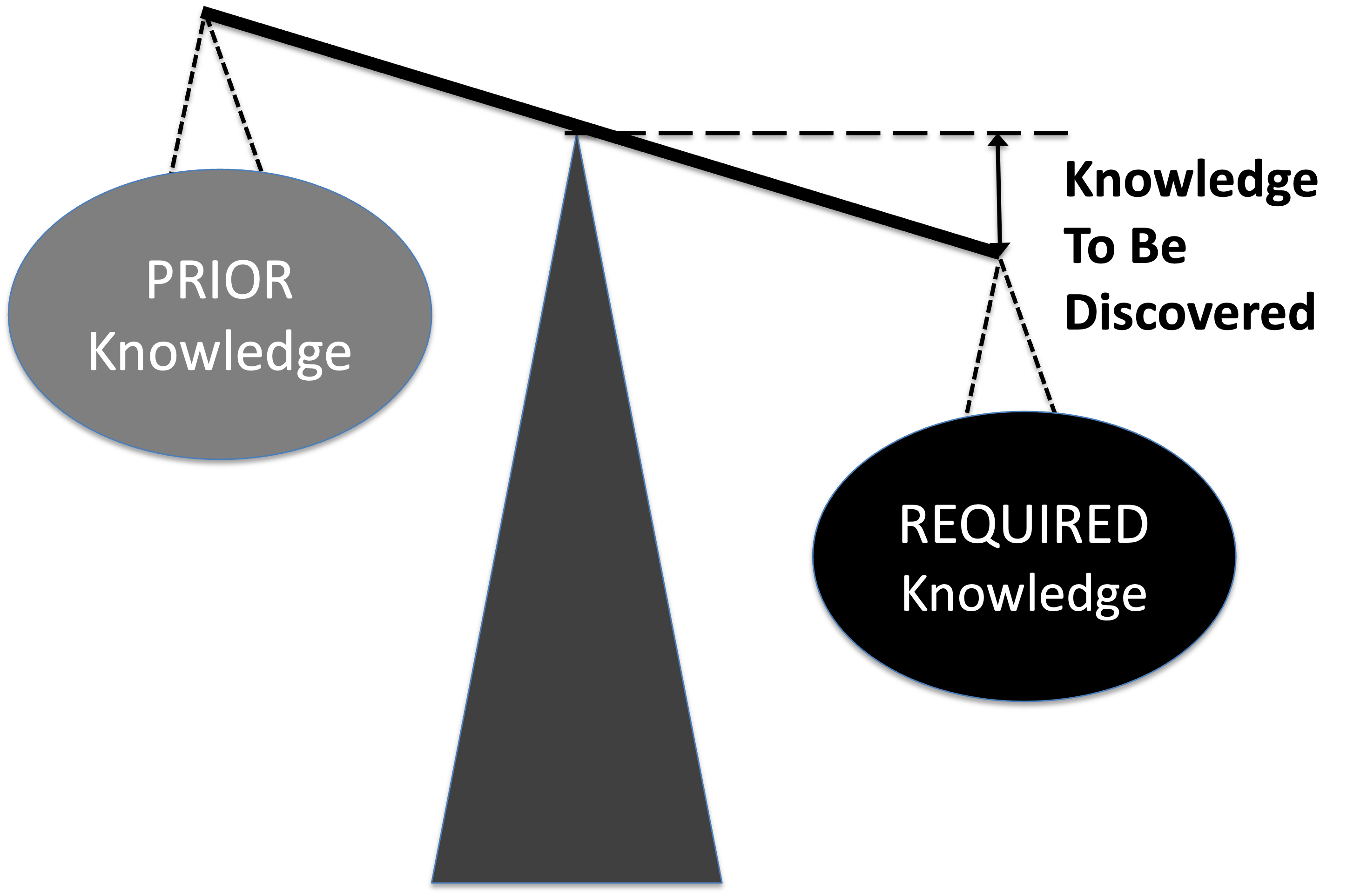
Imagine a scale: on one side is the required knowledge and on the other is the prior knowledge.
The gap between required and prior knowledge is the Knowledge to Be Discovered.
They will be balanced if they are equal, implying that the knowledge to be discovered equals zero.
When balanced, no further knowledge is needed; when imbalanced, knowledge acquisition is required.

"Knowledge to be discovered" captures several important aspects:

Potential for improvement: It suggests opportunity for better regulation through learning
Dynamic perspective: It implies that H(D|R) can be reduced over time as the regulator discovers more about the disturbances
Information-theoretic clarity: It directly connects to the information content - this is literally the information about disturbances that could potentially be gained
Cybernetic learning: It aligns with adaptive control concepts where systems improve by discovering patterns in disturbances
Constructive framing: Instead of focusing on what the regulator lacks, it emphasizes what could be gained

The term also creates a nice conceptual pairing:

Residual variety H(E) = what remains uncontrolled in outcomes
Knowledge to be discovered H(D|R) = what remains unknown about disturbances but could potentially be learned

This framing suggests that reducing "knowledge to be discovered" is a pathway to reducing "residual variety" - which is exactly the cybernetic insight that better information about disturbances enables better control. It emphasizes the constructive, learning-oriented aspect of cybernetic systems rather than just their current limitations.

5. Quantifying Knowledge To Be Discovered

How is the desired regulator to be brought into being? With whatever variety the components were initially available, and with whatever variety the designs (i.e. input values) might have varied from the final appropriate form, the maker Q acted in relation to the goal so as to achieve it. He therefore acted as a regulator. Thus the making of a machine of desired properties (in the sense of getting it rather than one with undesired properties) is an act of regulation[2].

Here we will model the relationship between the knowledge to be discovered H(D∣R) based on the observable outcomes E. We will be using Ashby's notation for disturbances D and regulation responses R. At some point they will be replaced with random variables X and Y respectively.

We use the following notation:

D = set of disturbances (inputs to the regulator)
R = set of responses (selections made)
T = set of outputs (produced tangible outputs)
E = set of outcomes (evaluated success/failure of the output)
H(D) = entropy of disturbances
H(R) = entropy of responses
H(E) = entropy of outcomes
H(R|D) = the conditional uncertainty about which action to choose from R for a given disturbance in D. H(R|D) = 0 represents the case of no uncertainty or complete knowledge, where the action is completely determined by the disturbance. H(R|D) = H(R) represents complete ignorance.
H(D∣R) = the residual uncertainty (variety) in disturbances after applying a regulator that had to be compensated by selection

We look at the case where the regulation was eventually successful. That is the knowledge discovery process closed the gap in internal variety that had to be compensated by selection i.e. eventually the knowledge to be discovered H(D|R) became 0.

The key idea is that the regulator's capacity to respond correctly is not static — it can change over time as the system learns and adapts. We model this using a time series of pairs (d_i, r_i), where d_i is the i-th disturbance and r_i is the i-th response. We then model the dynamics of the system over time using a time series of outcomes {e}= {e1 , . . . , ej}, where e_i is the outcome of the i-th disturbance-response (d_i, r_i) pair. E will be a sequence of {0,1}, where 0 = wrong output(failure to regulate) and 1 = correct output(successful selection). So the outcome vector in E becomes a performance trace: $E = (0, 1, 1, 1, 0, 0, 1, 1, 0, 1)$

We define a performance function:

θ (E) = \frac{1}{n} \sum_{i = 1}^{n} e_{i}

Where:

𝜃(E) is the success rate the regulator, i.e. the proportion of correct responses (1s) in the outcome vector E.
n is number of disturbance
e_i is outcome of the i-th disturbance (0 or 1)

This models the effectiveness of a regulator: the more 1s, the better they are at selecting the right response to a given disturbance. It also presents a dynamic improvement — the sequence of 0s and 1s in E can shift over time as the regulator improves (more 1s, fewer 0s).

Here are the assumptions our approach is based on:

For the knowledge discovery process there is some true value of the knowledge to be discovered H(X|Y).
The knowledge discovery process happens linearly as a constant stream of selections made by a regulator.
At n regular time intervals we sample from the output of the knowledge discovery process. A sample can contain either an output produced or nothing at all. If we sample nothing we assume there was a selection made by the regulator. In other words - we assume that if there is no output produced then there was a selection made. This way we divide the constant stream of selections made in n equally sized boxes.
The samples are independent of one another, hence the order of the outputs and selections is irrelevant.
Output T fully determines outcome E: producing an output guarantees 1, and missing guarantees 0. Under this assumption, E has the same distribution as T. H(E|T) = 0, an inevitable consequence of the fact that T fully determines E. H(E) depends solely on the probability distribution over E, which is determined by the success rate 𝜃.
Each output produced was the result of a dichotomous search in a search space M. In a dichotomous search, every “yes/no” decision halves the number of remaining possibilities, yielding one bit of information per step[9].
Thus the regulator always follows this optimal strategy to uncover the needed output in the minimum average number of selections.. That means the number of selections made per output produced equals the true value of the knowledge to be discovered H(X|Y)_M in the search space M.
At regular time intervals, a day or a week, we calculate the average number of selections per output by dividing the total number of selections made by the total number of outputs during the interval. It is a measure of the average H(X|Y) or "knowledge to be discovered" about each output, assuming that each selection contributes to reducing this uncertainty.
We know that the average number of selections per output equals the average knowledge to be discovered acquired by the underlying knowledge discovery process, because there is a mathematical theorem that supports this interpretation. The theorem states that the minimum average (expected) number of binary selections (also referred to as binary or yes/no questions) required to determine an output of a random variable X lies between H(X) and H(X) + 1 [5]. This theorem provides a connection between Shannon entropy (H) and the expected number of binary questions needed to acquire it.
Efficiency means the smaller the average number of selections made per output the better. In other words - the less knowledge to be discovered per output the more efficient the knowledge discovery process is.

We consider the example presented on Fig. 1: we have a regulator facing a sequence of disturbances D — it needs to select proper responses. The knowledge discovery process unfolds as a dynamic loop of regulation, selection, and feedback, culminating in the successful completion of the task. In the example, the regulator successfully produced 3 good outcomes, but required 6 additional regulatory interventions to handle disturbances for which internal variety was insufficient. Then, the regulator needed on average to make two selections in order to resolve one disturbance.

**Fig.1 A Knowledge Discovery Process.** Here we have a regulator facing a sequence of disturbances D — it needs to select proper responses. On the horizontal axis we have the progression of time measured in time intervals t. The unit of time for an interval t is the output duration time, also known as unit interval (UI) or the time to produce one output. The total available time T is divided into n time intervals t. In our example t equals 9 hence ***T=nt=9t***. At each time interval, the challenge is to produce the next output. This represents a disturbance that needs to be handled. The regulator responds by making selections to regulate the disturbance. At any given time the regulator can either make a selection in the selections channel or produce an output into the outputs channel. Each selection takes one time interval t and each output also takes one time interval t. We have three outputs produced - s₁, s₂ and s₃. For output s₁ there were two selections made q₁ and q₂. As per our assumptions that means output s₁ was the result of selections via dichotomous search in a search space M₁. Hence we have m₁=2²=4 and H₁=2 selections per output. For output s₂ there were two selections made q₃ and q₄. That means output s₂ was the result of elections via dichotomous search in a search space M₂. Hence we have m₂=2²=4 and H₂=2 selections per output. For output s₃ there were selections made q₅ and q₆. That means output s₃ was the result of elections via dichotomous search in a search space M₃. Hence we have m₃=2²=4 and H₃=2 selections per output. The average number of selections per output equals the average knowledge to be discovered H(D|R) acquired by the underlying knowledge discovery process in each of the search spaces M₁, M₂ and M₃. ***H(D|R)*** is also the average length of the full message “q1q2q3q4q5q6”. In this case we have three messages “q1q2”,”q3q4” and “q5q6” and their average length is 2.

We generalize the concept from Fig.1 as follows. Both channels (selections channel and outputs channel) form a time series {x} = {x₁ , . . . , x_n } of length n. We divide the time series {x} into S consecutive and non-overlapping subseries w_i, where S is the number of outputs in the time series {x} and i is the subseries index ranging from 1 to S. Each subseries w_i consists of one output s_i and zero or more selections {q_i} = {q₁ , . . . , q_j }, where j is in the interval [0,n/S]. Note, that each subseries w_i may have a different length. We count the number of selections q_i in each subseries w_i. Note that each subseries w_i contains only one output s_i. As per our assumptions, that means s_i was the result of a selection in a search space M_i. Next, we calculate the conditional missing information $H (d_{i} | r_{i})$ for each subseries w_i as equal to the number of selections q_i. After calculating the conditional missing information $H (d_{i} | r_{i})$ for each subseries, we construct a conditional missing information sequence { $H {(d | r)}_{i}$ } of length S.

Finally, the conditional missing information $H (X | Y)$ of the time series {x} is defined as the average of the conditional missing information sequence { $H {(d | r)}_{i}$ } in the form

$H (X | Y) = \frac{1}{S} \sum_{t = 1}^{S} H {(d | r)}_{i}$

(1)

We define the total number of selections made Q for time series {x} as the sum of the missing information sequence {H_i} in the form

$Q = \sum_{t = 1}^{S} H {(d | r)}_{i}$

(2)

Hence the average conditional missing information H equals the average number of selections made to produce one output.

$H (X | Y) = \frac{Q}{S}$

(3)

That is the same as the Information Rate formula, where Q is the Information Rate and S is the Outputs Rate.

We'd like to calculate H(X|Y) but we don't know Q - we know only S.

However in our model we assume that the minimum output duration is one unit of time and is equal to the time it takes to make one selection. If that's the case, then in our time-series model, each action (whether it's a selection 'q' or an output 's') could be considered as occupying one unit of time t. Hence the sum of S and Q as measured in time units equals the length n of the time series {x}:

$Q + S = n$

To apply the formula in practice we need to select a value for the length n of the time series {x}. The total available time T is implicitly contained in both Q and S.

$Q t + S t = T$

We define r as the output rate (whether it's a selection 'q' or a output 's') of the outputs channel S . r is measured in outputs per second and can be calculated using the output duration time t:

$n = \frac{T}{t} = T t^{- 1}$ $Q + S = \frac{T}{t}$ $r = t^{- 1}$

Then:

$Q + S = T r$

Now we have the length n of the time series {x} defined in terms of the total available time T and output rate r. We drop usage of n and instead from now on will be using N as maximum output rate.

$N = T r$

We generalize for the sum of selections Q, outputs S and the maximum output rate N.

$Q + S = N$

(4)

When we insert that in the formula for H(X|Y) we get:

$H (X | Y) = \frac{Q}{S} = \frac{N - S}{S} = \frac{N}{S} - 1$

Then, we have a formula that allows us to calculate the average knowledge to be discovered by selection H(X|Y) for a time series {x} if we know the maximum output rate N, the total available time T and the actual output rate S.

$H (X | Y) = \frac{N}{S} - 1$

(5)

If there is no knowledge to be discovered, i.e. there is no need to make selections at all, then S equals N and H is zero.

6. Generalizing KEDE

Here we generalize the Knowledge-Discovery Efficiency (KEDE) - scalar metric that quantifies how efficiently a system closes the gap between the variety demanded by its environment and the variety embodied in its prior knowledge[28]. This measure has the following properties:

It should be a function of the missing information H
Its maximum value should correspond to H equals zero i.e. there is no need to make selections, all knowledge is already discovered.
Its minimum value should correspond to H equals Infinity i.e. we have no knowledge to start with.
It should be continuous in the closed interval of [0,1]. This makes it very useful to be used as a percentage. This is because we need to be able to rank knowledge discovery processes by efficiency. The best ranked knowledge discovery process will have 100% and the worst 0%. That is practical and people are used to having such a scale.
It should be anchored to a natural constraint and thus support comparisons across settings and applications
It should be calculated per time period e.g. daily, weekly, quarterly, yearly
It should infer H(X|Y) solely from observable quantities of the tangible output we can measure

To capture all of that we generalize the metric named KEDE. KEDE is an acronym for KnowledgE Discovery Efficiency. It is pronounced [ki:d].

We rearrange the formula (5) to emphasize that KEDE is a function of either H(X|Y) or S and N:

$K E D E = \frac{1}{1 + H (X | Y)} = \frac{S}{N}$

(6)

KEDE from (6) contains only quantities we can measure in practice. KEDE also satisfies all properties we defined earlier. it has a maximum value of 1 and minimum value of 0; it equals 0 when H is infinite; it equals 1 when H is zero;

KEDE effectively converts the knowledge to be discovered H(X|Y), which can range from 0 to infinity, into a bounded scale between 0 and 1. KEDE is inversely proportional to the knowledge discovered. The more prior knowledge was applied the more efficient a Knowledge Discovery process is. Conversely, when a lot of required knowledge is missing then the knowledge discovery is less efficient.

KEDE is a measure of how much of the required knowledge for completing tasks is covered by the prior knowledge.

Below is an animated example of calculating KEDE when we search for a gold coin hidden in 1 of 64 boxes.

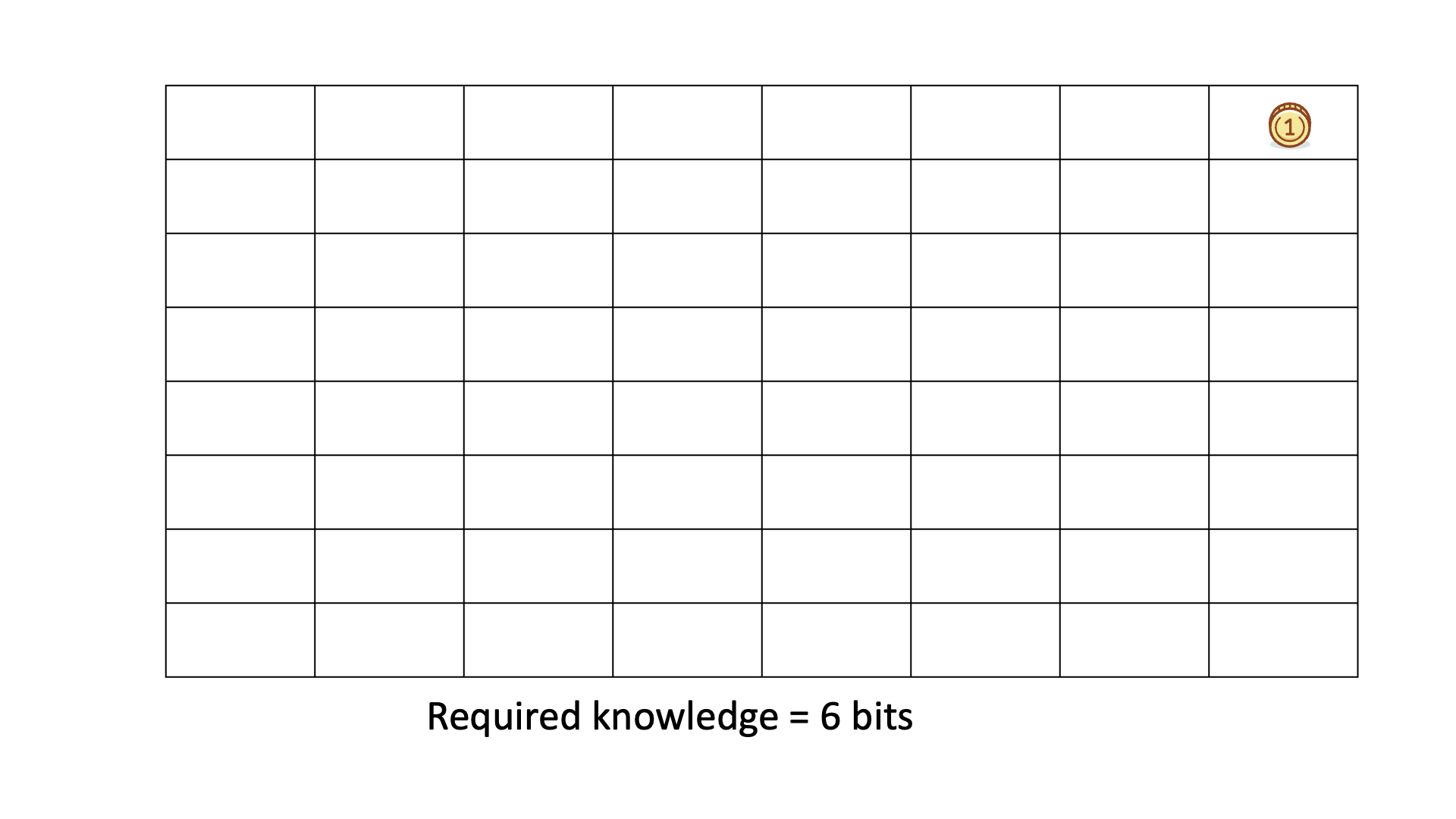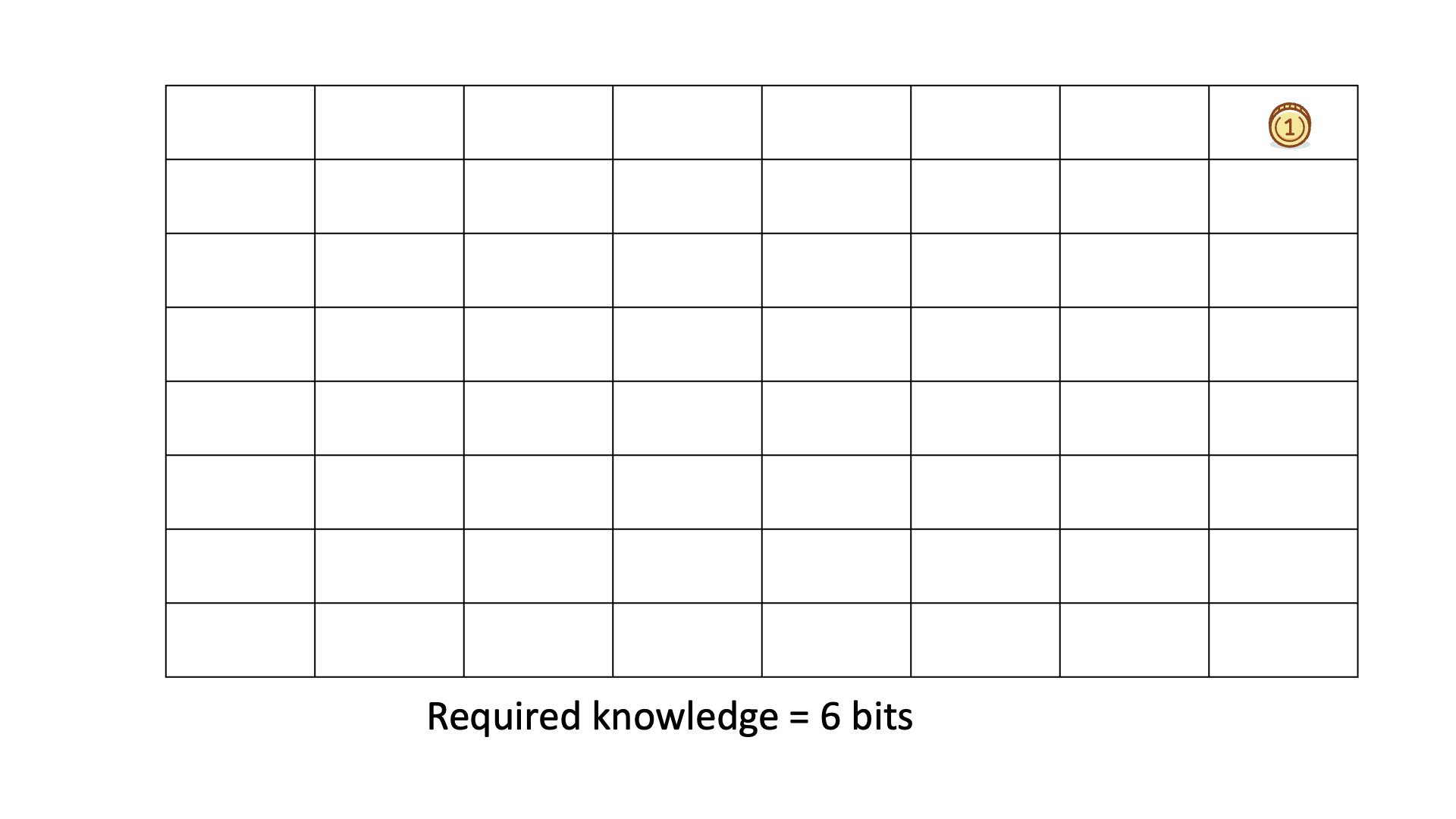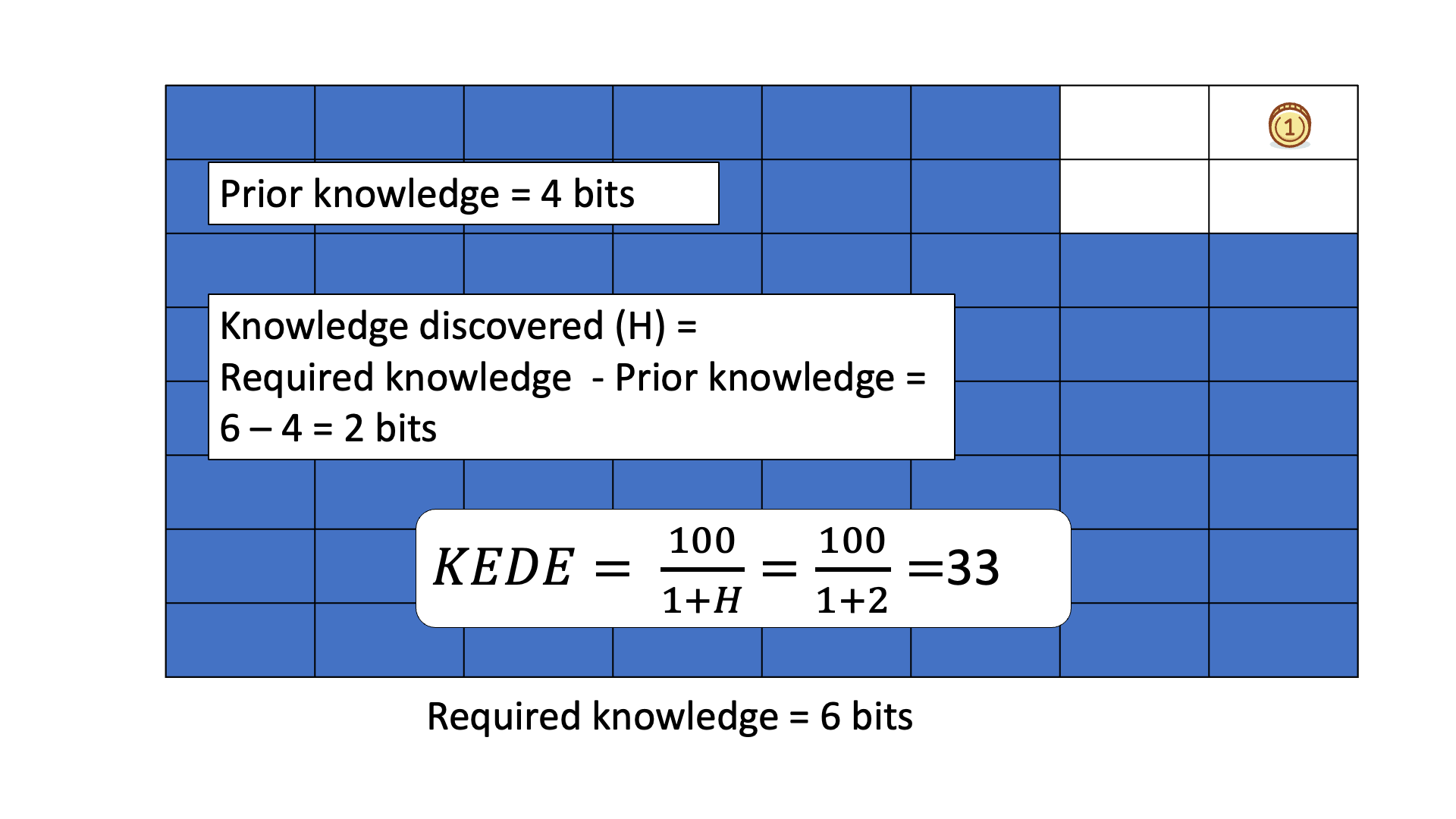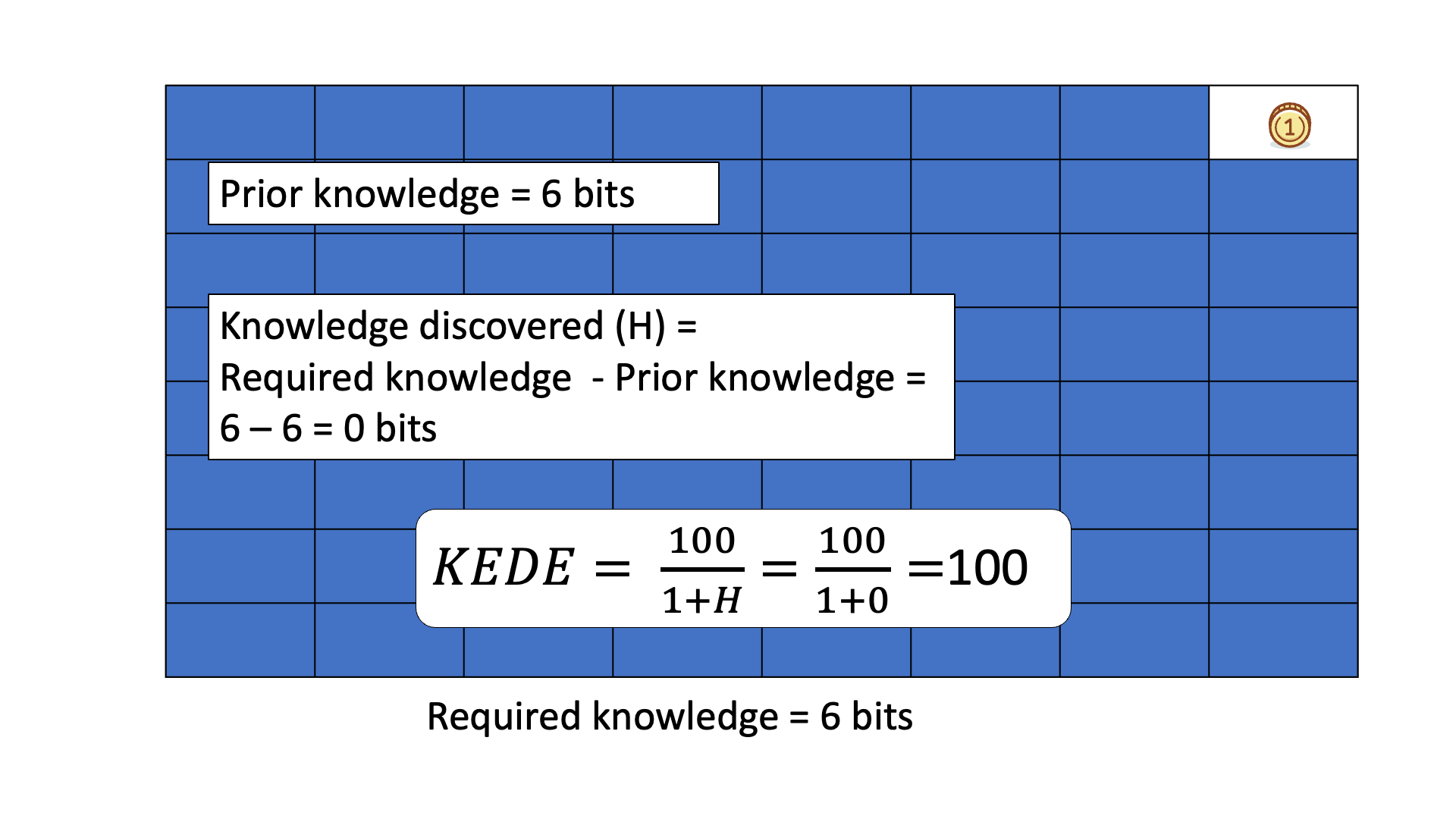
In all six cases the required knowledge is 6 bits. That means, we need to ask six binary selections (questions) on average to find the gold coin. We can see that the knowledge to be discovered depends on the prior knowledge. KEDE quantifies the knowledge discovered i.e. the difference between required knowledge and prior knowledge.

Due to its general definition KEDE can be used for comparisons between organizations in different contexts. For instance to compare hospitals with software development companies! That is possible as long as KEDE calculation is defined properly for each context. In what follows we will define KEDE calculation for the case of knowledge workers who produce textual content in general and computer source code in particular.

Anchoring KEDE to Natural Constraints

In our model, N is always the theoretical maximum output rate in an unconstrained environment, and S is the observed output rate under specific conditions over a given interval.

A key question is how to assign a natural constraint to N. That is, what constitutes an appropriate reference value for the maximum output rate?

We may turn to physics for an instructive analogy. A quantum (plural: quanta) represents the smallest discrete unit of a physical phenomenon. For instance, a quantum of light is a photon, and a quantum of electricity is an electron. In this context, the speed of light in a vacuum serves as a fundamental upper bound for N. However, identifying an analogous natural constraint for human activity—particularly knowledge work—presents greater challenges.

Consider the example of typing. Here, the quantum can reasonably be defined as a symbol, since it is the smallest discrete unit of text. A symbol may be a letter, number, punctuation mark, or whitespace character. To determine the appropriate bin width Δt, we refer to empirical data on the minimum time required to produce a single symbol. Typing speed has been subject to considerable research. One of the metrics used for analyzing typing speed is inter-key interval (IKI), which is the difference in timestamps between two keypress events. We see that IKI is defined equal to the symbol duration time t. Hence we can use the research of IKI to find the symbol duration time t. Studies have reported an average IKI of 0.238 seconds [26], yielding a maximum human typing rate of approximately N=1/t=1/0,238=4.2 symbols per second

A similar approach can be applied to tasks such as furniture assembly. In this case, a plausible quantum is a single screw tightened, since it represents a minimal, repeatable unit of output. We then identify Δt as the average time required to tighten one screw. Empirical studies report that this task typically takes between 5 and 10 seconds[34]. Using the upper bound, we estimate the maximum screw-tightening rate as N=1/t=1/10=0.1 screws per second.

This methodology offers a principled way to estimate N using domain-specific quanta and empirically grounded time durations, enabling the application of our model to a broad range of human tasks.

The next question concerns the appropriate definition of output for measuring S and N.

Both N and S can always be discretized—or “binned”—in a way that preserves the total information rate, regardless of whether the output arises from natural processes, human behavior, or machines. By choosing a bin width Δt small enough (e.g., milliseconds), the range of possible tangible outputs within each bin shrinks dramatically. This reduced range leads to less uncertainty in each bin, which compensates for the smaller time interval. Yet the ratio

\frac{total output in bin}{Δt}

remains an accurate measure of information rate.

As Δt becomes smaller, the measurements of S and N become more precise, as they reflect output over finer time intervals. But how small should Δt be? This dilemma is resolved by considering the granularity of outcomes associated with the output. The set E of outcomes can be thought of as the effects of the regulation process — the resulting states after the regulator responds to disturbances. In our model E is a sequence of {0,1}, where 0 = wrong output(failure to regulate) and 1 = correct output(successful selection). So the presence of a concrete outcome leads to a natural binning of the outputs, It also enables a clear distinction between signal (the entropy associated with producing the outcome) and noise (the residual variability unrelated to success or failure).

For example, two distinct symbols typed (e.g., ‘a’ vs. ‘b’) are clearly different outputs. However, if one symbol is typed in 91 milliseconds and another in 92 milliseconds, this minute variation is inconsequential to the outcome. Such timing fluctuations are typically unintentional, irrelevant to task performance, and should not be considered part of the output. In practical terms, if the theoretical upper bound N is known—for instance, 4.2 symbols per second as derived from human typing speed, and the observed rate is S=1 symbol per second, then time should be partitioned into one-second bins. Each bin then yields a single outcome: either 1 (a symbol was successfully typed) or 0 (no symbol typed or incorrect input).

This binning principle generalizes beyond typing. Whether analyzing foot strikes in trail running (where negligible spatial change occurs over milliseconds) or the discrete moves in solving a Rubik’s cube (where each turn resolves multiple potential states into a single action), binning ensures that no intermediate state need be modeled explicitly.

7. Applications

The knowledge-centric perspective builds on Ashby’s Law of Requisite Variety by emphasizing that successful outcomes depend not only on a system’s range of possible responses, but also on its ability to select the right response for each disturbance. This requires internal “system knowledge” that maps disturbances to appropriate actions. As Francis Heylighen proposed in his “Law of Requisite Knowledge,” effective regulation demands more than variety—it demands informed selection[29]. This knowledge-centric lens provides a foundation for analyzing how systems—biological, technical, or organizational—achieve control not just through options, but through understanding. The model we present operationalizes this perspective by estimating the informational requirements a system must satisfy to achieve its observed level of regulatory performance.

In what follows, we apply this knowledge-centric perspective to a range of domains, including motor tasks and manual assembly, industrial assembly lines, software development processes, speed of light in a medium, intelligence testing and sports performance. In each case, the model enables us to estimate, in bits of information, the amount of knowledge a system must lack to produce its observed level of performance. By quantifying the knowledge to be discovered H(X|Y), we assess how much uncertainty was there in the system’s ability to select appropriate responses. This allows us to compare systems not by tangible outputs, but by the hidden knowledge structures required to achieve them, offering a unified lens for analyzing adaptation, skill, and control across diverse contexts.

Tightening screws

We can apply our model to motor tasks such as furniture assembly. In this context, a natural unit of output — or “quantum” — is the tightening of a single screw.

Skilled workers engaged in manual assembly tasks can typically insert and tighten standard screws at a rate of 6–12 screws per minute under optimal, repetitive conditions — such as those found in furniture construction or industrial assembly lines. In contrast, automated screw-tightening machines can achieve significantly higher rates, often between 30 and 60 screws per minute [34] More complex manual tasks, such as high-torque applications involving ratchets or Allen keys, typically reduce the rate to 2–4 screws per minute due to the increased effort and precision required. In surgical or medical contexts, such as orthopedic screw insertion, accuracy and the avoidance of overtightening are paramount; here, rates often fall to 1–2 screws per minute, or approximately one screw every 30–60 seconds [46].

Context	Typical Rate (screws/minute)	Notes
Automated (machine)	30–60	For comparison, not manual
Fast, repetitive tasks	6–12	Assembly line, minimal torque required
High-torque/manual	2–4	Metalwork, ratchets, Allen keys
Surgical/precision	1–2	Orthopedic, high accuracy, low speed

The key observation is that rates decrease as torque, task complexity, or required precision increases. If we take the machine rate as the maximum possible output N and the observed human rate as S, we can estimate the average number of bits of information H(X∣Y) that the human operator must process per action.

KEDE = \frac{S}{N}

H (X | Y) = \frac{1}{K E D E} - 1 = \frac{N}{S} - 1 = \frac{60}{12} - 1 = 4 b i t s / s c r e w

This implies that the human must absorb approximately 4 bits of information, on average, to tighten a single screw under typical conditions.

The rate at which a person tightens screws depends on various factors, including:

Screw type and size
Material being fastened
Required torque
Tool used (screwdriver, ratchet, etc.)
Operator skill and fatigue

These constitute the disturbance variety D faced by the human operator. The operator, acting as a regulator, responds with selections from their internal repertoire of skills — the regulatory variety R.

This interpretation aligns with existing research, which suggests that task difficulty directly influences the amount of information a task imparts [47, 48]. When difficulty is appropriately matched to the individual’s skill level, the task yields maximal informational value [49], and the time required reflects the interaction between task complexity and the individual's regulatory capacity [50].

Using our model, we transform a sequence of real-world actions in furniture assembly into a granular, time-based measure of regulatory capacity. This enables us to quantify — in bits — how much variety the individual must absorb in order to successfully complete the task.

Typing the longest English word

Let's use an example scenario to see Ashby’s law applied to human cognition and knowledge work.

For that we'll have myself executing the task of typing on a keyboard the word “Honorificabilitudinitatibus”. It means “the state of being able to achieve honours” and is mentioned by Costard in Act V, Scene I of William Shakespeare's “Love's Labour's Lost”. With its 27 letters “Honorificabilitudinitatibus” is the longest word in the English language featuring only alternating consonants and vowels.

The way I will execute this task is to go to the "play text" or "script" of “Love's Labour's Lost”, look up the word and type it down. The manual part of the task is to type 27 letters. The knowledge part of the task is to know which are those 27 letters.

In order to track the knowledge discovery process I will put "1" for each time interval when I have a letter typed and "0" for each time interval when I don't know what letter to type.

I start by taking a good look at the word “Honorificabilitudinitatibus” in the script of “Love's Labours' Lost”. That takes me two time intervals. Then I type the first letters “H”, “o”, and “n”.I continue typing letter after letter: “o”, “r”. At this point I cannot recall the next letter. What should I do? I am missing information so I go and open up the script of “Love's Labours Lost” and I look up the word again. Now I know what the next letter to type is but acquiring that information took me one time interval. This time I have remembered more letters so I am able to type “i”,”f”,”i”,”c”,”a”,”b”,”i”. Then again I cannot continue because I have forgotten what were the next letters of the word, so I have to look it up again.in the script. That takes two more time intervals. Now I can continue my typing of “l”,”i”,”t”. At this point I stop again because I am not sure what were the next letters to type, so I have to think about it. That takes one time interval. I continue my typing with “u”,”d”,”i”. Then I stop again because I have again forgotten what were the next letters to type, so I have to look it up again in the script of “Love's Labours Lost”. That takes two more time intervals. Now I know what the next letter to type is so I can continue typing “n”,”i”.At this point I cannot recall the next letter. so I have to look it up again in the script. That takes two more time intervals. After I know what the next letter to type is I can continue typing “t”,”a”,”t”,”i”,”b”,”u”,”s”. Eventually I am done!

At the end of the exercise I have the word “Honorificabilitudinitatibus” typed and along with it a sequence of zeros and ones.

		H	o	n	o	r		i	f	i	c	a	b	i			l	i	t		u	d	i			n	i			t	a	t	i	b	u	s
0	0	1	1	1	1	1	0	1	1	1	1	1	1	1	0	0	1	1	1	0	1	1	1	0	0	1	1	0	0	1	1	1	1	1	1	1

In the table we have separated the manual work of typing from the knowledge work of thinking about what to type.

We made visible both the manual work and the knowledge discovery parts of a Knowledge Discovery process.

The first row of the table shows the knowledge I manually transformed into tangible output - in this case the longest English word. The second row of the table shows the way I discovered that knowledge. There is a "0" for each time interval when I was missing information about what to type next. There is "1" for each time interval when I had prior knowledge about what to type next. Each "0" represents a selection I needed to ask in order to acquire the missing information about what letter to type next. Each "1" represents prior knowledge.

We know that there is knowledge applied when we see the tangible output of the process. We know there was knowledge discovered when we see there was at least one selection made.

In the exercise above we witnessed the discovery and transformation of invisible knowledge into visible tangible output.

KEDE calculation

We can calculate the KEDE for this sequence of outcomes.

K E D E = \frac{S}{N} = \frac{27}{37} = 0.73

We can also calculate the knowledge discovered H(X|Y) in bits of information.

H (X | Y) = \frac{N}{S} - 1 = \frac{37}{27} - 1 = 0.37

We’ve turned a real-world sequence of action and hesitation into a fine-grained, time-based measurement of your regulatory capacity — effectively measuring how much variety I needed to absorb with external help i.e. my knowledge discovered.

Measuring software development

In order to use the KEDE formula (6) in practice we need to know both S and N. We can count the actual number of symbols of source code contributed straight from the source code files. For N we want to use some naturally constrained value.

N is the maximum number of symbols that could be contributed for a time interval by a single human being.

In the below formula for N we want to use some naturally constrained value: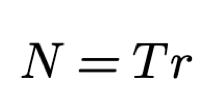

To achieve this, the following estimation is performed. We pick T = 8 hours of work because that is the standard length of a work day for a software developer.

To calculate the value of r we need to pick the symbol duration t.

The value of the symbol duration time t is determined by two natural constraints:

the maximum typing speed of human beings
the capacity of the cognitive control of the human brain

Typing speed has been subject to considerable research. One of the metrics used for analyzing typing speed is inter-key interval (IKI), which is the difference in timestamps between two keypress events. We see that IKI is defined equal to the symbol duration time t. Hence we can use the research of IKI to find the symbol duration time t. It was found that the average IKI is 0.238s [26]. There are many factors that affect IKI [6]. It was also found that proficient typing is dependent on the ability to view characters in advance of the one currently being typed. The median IKI was 0.101s for typing with unlimited preview and for typing with 8 characters visible to the right of the to-be-typed character but was 0.446s with only 1 character visible prior to each keystroke [7]. Another well-documented finding is that familiar, meaningful material is typed faster than unfamiliar, nonsense material[8]. Another finding that may account for some of the IKI variability is what may be called the “word initiation effect”. If words are stored in memory as integral units, one may expect the latency of the first keystroke in the word to reflect the time required to retrieve the word from memory[9].

Cognitive control, also known as executive function, is a higher-level cognitive process that involves the ability to control and manage other cognitive processes that permit selection and prioritization of information processing in different cognitive domains to reach the capacity-limited conscious mind. Cognitive control coordinates thoughts and actions under uncertainty. It's like the "conductor" of the cognitive processes, orchestrating and managing how they work together. Information theory has been applied to cognitive control by studying the capacity of cognitive control in terms of the amount of information that can be processed or manipulated at any given time. Researchers found that the capacity of cognitive control is approximately 3 to 4 bits per second[32][33], That means cognitive control as a higher-level function has a remarkably low capacity.

Based on the above research we get:

Maximum typing speed of human beings to be r=1/t=1/0,238=4.2 symbols per second
Capacity of the cognitive control of the human brain to be approximately 3 to 4 bits per second. Since we assume one question equals one bit of information we get 3 to 4 questions per second.
Asking questions is an effortful task and humans cannot type at the same time. If there was a symbol NOT typed then there was a question asked. That means the question rate equals the symbol rate, as explained here.

Since the question rate needs to equal the symbol rate we consider that 4.2 symbols per second is a rate higher than 3 to 4 bits per second. We need to get a symbol rate between 3 and 4 symbols per second.

In order to get a round value of maximum symbol rate N of 100 000 symbols per 8 hours of work we pick symbol duration time t to be 0.288 seconds. That is a bit larger than what the IKI research found but makes sense when we think of 8 hours of typing. Having t of 0.288 seconds makes a symbol rate r of 3.47 symbols per second. That is between 3 and 4 and matches the capacity of the cognitive control of the human brain.

We define CPH as the maximum rate of characters that could be contributed per hour. Since r is 3.47 symbols per second we get CPH of 12 500 symbols per hour. We substitute T = h and r=CPH and the formula for N becomes:

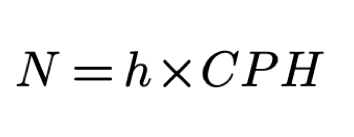
where h is the number of working hours in a day and CPH is the maximum number of characters that could be contributed per hour. We define h to be eight hours and get N to be 100 000 symbols per eight hours of work.

Total working time consist of four components:

Time spent typing (coding)
Time spent figuring out WHAT to develop
Time spent figuring out HOW to code the WHAT
Time doing something else (NW)

Let us assume an ideal system where the time spent doing something else T_NW is zero. Using the new formula for N the formula for H becomes

Note, that since N is calculated per hour so S also needs to be counted in an hour.

We see that the more symbols of source code contributed during a time interval the less missing information was there to be acquired. We want to compare the performance of different software development processes in terms of the efficiency of their knowledge discovery processes. Hence we rearrange the formula to emphasize that.

$\frac{S}{h \times C P H} = \frac{1}{1 + H}$

(7)

The right hand part is the KEDE we defined earlier. Thus, we define an instance of the metric KEDE - the general metric that we introduced earlier. This version of KEDE is for the case of knowledge workers that produce tangible output in the form of textual content:

$K E D E = \frac{S}{h \times C P H}$

(8)

KEDE from (8) contains only quantities we can measure in practice. KEDE also satisfies all properties we defined earlier. it has a maximum value of 1 and minimum value of 0; it equals 0 when H is infinite; it equals 1 when H is zero; it is anchored on a natural constraint—the maximum typing speed of a human being.

If we convert the KEDE formula into percentages then it becomes:

$K E D E = \frac{S}{h \times C P H} \times 100 %$

(9)

We can use KEDE to compare the knowledge discovery efficiency of software development organizations.

Testing Intelligence

Today all measure intelligence by the power of appropriate selection (of the right answers from the wrong). The tests thus use the same operation as is used in the theorem on requisite variety, and must therefore be subject to the same limitation. (D, of course, is here the set of possible questions, and R is the set of all possible answers). Thus what we understand as a man’s “intelligence” is subject to the fundamental limitation: it cannot exceed his capacity as a transducer. (To be exact, “capacity” must here be defined on a per-second or a per-question basis, according to the type of test.)[3]

We can also use our model to the testing of human and AI intelligence. We infer this capacity from performance under variety — i.e., how many different problems a system or a person can solve correctly.

The dominant mathematical models for testing intelligence by the number of answered problems are benchmark datasets like MMLU, GSM8K, MATH, and FrontierMath. These models measure intelligence by the raw count or percentage of correctly solved problems, with more advanced benchmarks designed to minimize guessing and require deep reasoning.

From the knowledge-centric perspective:

The disturbances are the questions $Q = {q_{1}, q_{2}, q_{3}, . . . q_{n}}$
The person gives responses $R = {r_{1}, r_{2}, r_{3}, . . . r_{n}}$
The outcomes are $E = {e_{1}, e_{2}, e_{3}, . . . e_{n}} \in {0, 1}$

So: Intelligence is the capacity to consistently produce 1s in E, despite the variety in D.

Several mathematical models and benchmark datasets are used to evaluate intelligence—especially artificial intelligence (AI)—by measuring the number and complexity of math problems answered correctly. These models serve as standardized tests for both AI and, by analogy, human intelligence[52].

Massive Multitask Language Understanding (MMLU):

MMLU is a widely used benchmark that tests AI models on a broad range of subjects, including mathematics at various levels (high school, college, abstract algebra, formal logic).
The test is typically formatted as multiple-choice questions, and performance is measured by the percentage of correct answers out of the total number of questions
For example, advanced AI models have achieved up to 98% accuracy on math sections of MMLU, indicating high proficiency in standard math tasks but not necessarily deep reasoning

Grade School Math 8K (GSM8K)

GSM8K is a dataset of 8,500 high-quality, grade school-level word problems designed to test logical reasoning and basic arithmetic skills.
Evaluation is based on exact match accuracy: the number of problems answered exactly correctly divided by the total number attempted
This benchmark is used to assess step-by-step reasoning and the ability to handle linguistic diversity in problem statements.

MATH (Mathematics Competitions Dataset)

MATH consists of problems from high-level math competitions (e.g., AMC 10, AMC 12, AIME), focusing on advanced reasoning rather than rote computation.
Performance is measured by the percentage of correct answers, with human experts (e.g., IMO medalists) providing a reference for top-level performance
The dataset is challenging for both humans and AI, with LLMs typically scoring much lower than expert humans.

FrontierMath[53]

FrontierMath is a new benchmark featuring hundreds of original, expert-level math problems spanning major branches of modern mathematics.
Problems are designed to be "guessproof" and require genuine mathematical understanding, with automatic verification of answers
The benchmark is used to assess how well AI models can understand and solve complex mathematical problems, similar to human performance.

In human intelligence testing, Psychometric models such as IQ tests or psychometric approaches also use the number of correctly answered problems as a key metric. These tests are standardized, and the raw score (number of correct answers) is often converted into a scaled score or percentile.

As an example we will use the Exact Match metric as the evaluation method[52]. Given that each question in our benchmark dataset has a single correct answer and the model produces a response per query, Exact Match ensures a rigorous evaluation by comparing the extracted answer to the ground truth.

Let $ŷ_{i}$ represent the extracted answer from the model's output for the $i^{th}$ question, and let $y_{i}$ be the corresponding ground truth answer. The Exact Match accuracy is computed as:

$Exact Match (%) = \frac{\sum_{i = 1}^{N} 𝟙 (normalize (ŷ_{i}) = normalize (y_{i}))}{N} \times 100$

where:

$N$ is the total number of evaluated questions.
$𝟙 (\cdot)$ is the indicator function, returning 1 if the extracted model response matches the ground truth after preprocessing, and 0 otherwise.
$normalize (\cdot)$ is a function that standardizes formatting, trims spaces, and normalizes numerical values.

The knowledge discovery efficiency of an LLM can be calculated as:

Exact Match accuracy = \frac{S}{N} = KEDE

where S is the number of correct answers and N is the total number of evaluated questions..

Let's pick the case of the performance of GPT-4o on the MATH benchmark, which achieved a significantly lower accuracy of 64.88%, lagging behind its peer models[52]. Now, we can calculate the average knowledge discovered H(X|Y).

H (X | Y) = \frac{1}{K E D E} - 1 = \frac{100}{64.88} - 1 = 1.54 b i t s / problem

Basketball Game

We can also use this model to assess the performance of a basketball player.

Timeframe is a basketball game.
We observe N total shot attempts.
S of them are successful (shot made).
We record a binary outcome sequence $E \in {0, 1}^{N}$
The empirical success rate: $θ = \frac{S }{N}$ is our observed probability of success.

Interpretation using Ashby’s Law

The basketball shot is a regulation problem: the player must control their body and respond to the game environment to produce the desired outcome. The player is faced with a series of disturbances (D) in the form of different shots to make under different conditions. The player responds with a selection, drawn from their internal skills (regulatory variety R) in the form of different shooting techniques. Each shot is uncertain whether it will be successful. The outcome E is whether the shot is made (1) or missed (0).

Over N shots, the success rate $θ = \frac{S }{N}$ reflects how often the player's internal variety is sufficient to absorb the variety in the environment — an operational measure of regulatory success.

In this case, θ becomes a practical proxy for how often the regulator (player) has sufficient internal variety to absorb the disturbance presented by the game. However, it is important to note that this is a simplified model and does not account for all the complexities of basketball performance. For example, the player may have different success rates depending on the type of shot, the position on the court, or the level of defense. These factors can all affect the player's ability to regulate their performance and should be considered when interpreting the results. Thus, as explained here θ is a useful heuristics for P(E=1), but the full picture includes the quality of mapping, not just quantity.

Applying the Model

NBA keeps track of field goal attempts and makes for each player. The most field goal attempts by a player in a single NBA game is 63, achieved by Wilt Chamberlain during his legendary 100-point game against the New York Knicks on March 2, 1962 We take this as the natural constraint so N=63. We can also take the number of successful shots S=36, which is the most field goals made in a single game by a player[13].

We can calculate the KEDE for this sequence of outcomes.

K E D E = \frac{S}{N} = \frac{36}{63} = 0.571

We can also calculate the knowledge discovered H(X|Y) in bits of information.

H (X | Y) = \frac{N}{S} - 1 = \frac{63}{36} - 1 = 0.75

That means that the player needed to absorb 0.75 bits of information on average to make the shot.

We’ve turned a real-world sequence of basketball shots into a fine-grained, time-based measurement of a regulatory capacity — effectively measuring how much variety the player needed to absorb.

We can also use this model to assess the performance of a basketball team. In this case the success rate coincides with the field goal percentage (FG%) of the team which is the percentage proportion of made shots over total shots that a player or a team takes in games. There is a statistical distribution for NBA field goal percentage (FG%) [10]. Analysts and researchers often study the distribution of FG% across players or teams to understand scoring efficiency and trends[11]. The NBA record for the highest FG% in a single game by a team is 69.3%, set by the Los Angeles Clippers on March 13, 1998, when they made 61 of 88 shots[12].

For example, in the 2023-24 season, team FG% ranged from about 43.5% (lowest) to 50.6% (highest), with the league average typically falling in the mid-to-high 40% range[11]. if we take the average FG% of 45% , we can calculate the average knowledge discovered H(X|Y).

H (X | Y) = \frac{1}{K E D E} - 1 = \frac{1}{F G %} - 1 = \frac{1}{0.45} - 1 = 1.22

That means that a team needed to absorb 1.22 bits of information on average to make a shot.

Assembly Line

We can also use this model to assess the knowledge discovery efficiency of an assembly line.

The assembly line is a system that transforms raw materials into finished products. The assembly line has a set of disturbances (D) in the form of different raw materials, machines, and processes. The assembly line responds with a selection, drawn from its internal structure (R) in the form of different machines, processes, and workers.

From a knowledge-sentric perspective most of the knpwledge discovery happens in the design phase of the assembly line. This is the planning for design, fabrication and assembly. This activity has also been called design for manufacturing and assembly (DFM/A) or sometimes predictive engineering. It is essentially the selection of design features and options that promote cost-competitive manufacturing, assembly, and test practices[51]. Thus most of the disturbances D are already absorbed by the design of the assembly line. That means when the workers have most of the knowledge built into the assembly line and the operational procedures.

Assembly line efficiency (AE) is the ratio of the output to the maximum possible output, often expressed as a percentage.

The efficiency of the assembly line can be calculated as:

AE = \frac{S}{N} = KEDE

where S is the actual output and N is the maximum possible output.

We can assume that an assembly line is designed to produce a certain number of successful products (S) with a maximum rate of N products per hour. So for example, a shoe manufacturer has an actual output of 100 shoes per day, and a maximum potential output of 120 shoes per day. Their production line efficiency would be 83%. Now, we can calculate the average knowledge discovered H(X|Y).

H (X | Y) = \frac{1}{K E D E} - 1 = \frac{1}{A E} - 1 = \frac{100}{83} - 1 = 0.2 b i t s / s h o e

To optimize the AE, companies can apply DFA guidelines, such as minimizing the number and variety of parts, standardizing the fasteners and connectors, and simplifying the assembly sequence and orientation[51].

Interpreting the results involves a comprehensive analysis of the data to understand where and why inefficiencies occur. In general, the higher the AE, the better the design. On the other hand, AE close to 100% might indicate under-utilised capacity. It’s essential to compare high efficiency with industry capacity standards to determine if an increase in production is feasible and beneficial.

If AE is consistently below industry benchmarks, this could highlight several potential issues:

Machinery: It may indicate that machines are outdated, malfunctioning, or not suitable for the required tasks.
Labour Skills: Low efficiency might be due to workforce training gaps.
Process Design: Sometimes, the workflow or layout of the production line itself causes inefficiencies.

Speed of Light in Medium

We can also use this model to support an interpretation of Ashby's Law of Requisite Variety to assess the speed of light in a medium where the medium acts as a disturbance to photon flow. Here's how this perspective aligns with the physics of light-matter interactions:

Disturbance: The medium's atomic/molecular structure introduces spatial and electromagnetic inhomogeneities (e.g., refractive index variations, turbulence).
Control Mechanism: Photons' ability to "counteract" disturbances through wavelength compression and phase synchronization.
Requisite Variety: Photons require sufficient adaptability (e.g., frequency range, polarization states) to navigate the medium's complexity without scattering or losing coherence.

The speed of light in a vacuum is 299,792,458 m/s. In a medium, the speed of light is reduced by a factor n, called the refractive index defined as:

n = \frac{c}{v}

where c is the speed of light in vacuum and v is the speed of light in the medium.

The refractive index is a measure of how much the speed of light is reduced in the medium. The higher the refractive index, the more the speed of light is reduced.

For example, the refractive index of water is 1.33, which means that the speed of light in water is:

v = \frac{299 792 458}{1.33} \approx 225 000 000 m / s

The knowledge discovery efficiency of the speed of light in a medium can be calculated as:

K E D E = \frac{v}{c} = \frac{1}{n}

where v is the actual speed of light in the medium and c is the maximum possible speed of light in vacuum.

Now, we can calculate the average knowledge discovered H(X|Y) by a photon in water:

H (X | Y) = \frac{1}{K E D E} - 1 = \frac{1}{\frac{1}{n}} - 1 = n - 1 = 1.33 - 1 = 0. 33 b i t s / p h o t o n

Appendix

Is it correct that P(E=1)= R/D?

The probability P(E=1) (i.e., the chance of selecting the correct answer) is related to R and D, but not necessarily a simple ratio like R/D in all cases.

When it is roughly correct

If:

D is the number of distinct disturbances
R is the number of distinct, appropriate responses available to the regulator
Each disturbance has one correct matching response
And the regulator picks uniformly at random from R, or can respond appropriately only to a fraction R/D

Then:

P ((E = 1) \approx \frac{R}{D} ​

This would mean the regulator can respond correctly to R out of D possible cases. So if the regulator is only capable of matching 4 out of 10 possible disturbances with appropriate answers, then the chance of success on a random question is 4/10=0.4.

When it's not exactly correct

In real-world or more nuanced models:

R and D are not always directly countable or uniform.
The relationship depends on how well R matches D — not just their sizes.
Some regulators may have R=D in cardinality but poor mappings (i.e., wrong associations).
Or the regulator may be probabilistic or partially adaptive, changing over time.
The mapping between disturbances and responses may not be uniform.
Some disturbances may have multiple correct responses, or some responses may apply to multiple disturbances.
The regulator may have varying levels of expertise or knowledge, affecting their ability to respond correctly.
The regulator may not pick uniformly at random from R, but rather use heuristics or biases.

So in general, we say:

P (E = 1) = \sum_{d \in D}^{} P (d) P (c o r r e c t r | d)

Where:

P(d): probability of a disturbance
P(correct r|d): probability of a correct response given a disturbance
The sum is over all disturbances in D.
This captures the idea that the probability of a correct response depends on both the distribution of disturbances and the regulator's ability to respond correctly.

Same applies to H(R)/H(D)

Variety can also be defined using logarithmic (information-theoretic) measure in terms of log₂(number of distinguishable states) — i.e., entropy.

The ratio $\frac{H (R)}{H (D)}$ is a normalized ratio — showing what fraction of the required variety the regulator can provide.

If $\frac{H (R)}{H (D)} = 1$ , then regulator has exactly enough variety to match disturbances
If <1, then the regulator can only match a fraction of the disturbances.
If >1, then the regulator has more variety than needed to match disturbances.

This ratio is not exactly equal to P(E=1), but it tells us how well-positioned the system is to achieve a high P(E=1). Here's the subtle but important distinction:

P(E=1) is a probability of success, while $\frac{H (R)}{H (D)}$ is a ratio of variety.
The ratio is a structural or potential measure: how much capability the regulator has in theory It gives a sense of how much variety the regulator has relative to the disturbances.
The probability of success is a performance measure: how often it actually selects the correct answer. It gives a sense of how likely it is that the regulator will succeed in matching the disturbances.

\frac{H (R)}{H (D)}

is a useful approximation of the probability of success, but it doesn't capture all the nuances of the mapping between disturbances and responses.

So, while $\frac{H (R)}{H (D)}$ does not equal P(E=1), the two are strongly correlated, especially under ideal conditions as presented earlier.

Conclusion

If we normalize and treat this probabilistically, yes — the fractions $\frac{R}{D}$ and $\frac{H (R)}{H (D)}$ are useful heuristics for P(E=1), but the full picture includes the quality of mapping, not just quantity.

If the regulator has perfect variety and mapping, then P(E=1)=1.
If the regulator has limited variety, the probability goes down - which is what $\frac{R}{D}$ and $\frac{H (R)}{H (D)}$ are trying to capture.

We have to recognize that intelligent behavior requires both sufficient variety R and correct mappings between D and R

H(D|R) Dynamic Modeling Across Time

There is mathematical modeling for dynamic cases where the effectiveness of the regulator changes over time. This involves tracking the changes in conditional entropy ( H(D|R) ) as the regulator improves its ability to handle disturbances.

Let’s define:

$t \in (t_{0}, t_{n})$ : discrete or continuous time
$H_{t} (D | R)$ : conditional entropy at time $t$
$R_{t}$ : regulator’s state or variety at time $t$
$D_{t}$ : disturbance pattern at time $t$

Then we can model:

H_{t} ​ (D | R) = \sum_{d \in D ​_{t}, r \in R_{t}}^{} P (d, r) \log_{2} (\frac{P (d, r)}{P (r)})

We can track $H_{t} (D | R)$ over time to represent adaptive learning or regulatory tuning.

Example: Dynamic Modeling of H(D|R)`

Let's consider two time points:

Time 1 (t₁): The regulator is not effective, and H(D|R) is high.
Time 2 (t₂): The regulator becomes effective, and H(D|R) is minimized (approaches 0).

Mathematical Representation

We can represent this dynamic modeling as:

Time 1 (t₁)

At t₁:
- The regulator's variety (R) is insufficient to handle the disturbances (D).
- The conditional entropy H(D|R) is high, indicating high uncertainty in disturbances given the responses.

Time 2 (t₂)

At t₂:
- The regulator's variety (R) has improved and is now sufficient to handle the disturbances (D).
- The conditional entropy H(D|R) is minimized (approaches 0), indicating low uncertainty in disturbances given the responses.

Conclusion

This dynamic case modeling shows how the conditional entropy ( H(D|R) ) changes as the regulator improves its ability to handle disturbances. Initially, ( H(D|R) ) is high, indicating high uncertainty. As the regulator becomes more effective, ( H(D|R) ) approaches 0, indicating low uncertainty and better management of disturbances.

Selection as a Staged Process

Rather than a single act, selection is often staged — especially in real-world cognition and decision-making. Think of it as progressively reducing uncertainty at each stage — each stage reduces the complexity for the next:

Field of Possibilities
- We start with a wide array of potential options.
- This is your "state of uncertainty" — maximum entropy.
Preliminary Selection / Filtering
- Some options are ruled out based on prior knowledge, context, or constraints. For example, if we’re trying to diagnose a health condition and we know the patient is male, we eliminate conditions exclusive to females.
- This reduces the entropy, but not to zero.
Refinement / Further Selection
- We apply more specific criteria to narrow down the options further. This could involve using testing, exploration, or weighing pros and cons. heuristics, rules of thumb, or even machine learning algorithms.
- This is where we start to get closer to the "correct" answer.
Final Selection
- We make a final choice based on the refined set of options — one that is contextually appropriate and guided by purpose or relevance. .
- This is where information becomes knowledge — it’s no longer just raw data; it has been integrated and acted upon.
- This is the point where we achieve the lowest entropy — ideally, we have a clear answer.
Materialization and Use
- The selected outcome can be material e.g. a symbol written down, or affects behavior that has material consequences e.g. actions.
- This is when knowledge has agency — it enables action or understanding.

How to cite:

Bakardzhiev D.V. (2025) Knowledge Discovery Efficiency (KEDE) and Ashby's Law https://docs.kedehub.io/kede/kede-ashbys-law.html

Works Cited

1. Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal. 1948;27(3):379-423. doi:10.1002/j.1538-7305.1948.tb01338.x

2. Ashby, W.R. (1956). An Introduction to Cybernetics; Chapman & Hall,

3. Ashby, W. R. (2011). Variety, Constraint, And The Law Of Requisite Variety. 13, 18.

4. MacKay, D. M. (1950). Quanta! aspects of scientific information. Philosophical Magazine; 41, 289-311;

5. Cover, T. M. and Thomas, J. A. (1991), Elements of Information Theory, John Wiley and Sons, New York. page.95 in 5.7 SOME COMMENTS ON HUFFMAN CODES

6. Wheeler, J. A. (1990). Information, physics, quantum: The search for links. In W. H. Zurek (Ed.), Complexity, entropy, and the physics of information (Vol. 8, pp. 3–28). Taylor & Francis.

7. Yaneer Bar-Yam.(2004) Multiscale variety in complex systems. Complexity, 9(4):37{45,

8. Ashby, W.R. (1991). Requisite Variety and Its Implications for the Control of Complex Systems. In: Facets of Systems Science. International Federation for Systems Research International Series on Systems Science and Engineering, vol 7. Springer, Boston, MA. https://doi.org/10.1007/978-1-4899-0718-9_28

9. Shannon, C. E. Communication theory of secrecy systems. Bell System technical Journal, 28, 656-715, 1949

10. Kubatko J, Oliver D, Pelton K, et al. A starting point for analyzing basketball statistics. J Quant Anal Sports 2007; 3: 1–22.

11. Sports Reference LLC. "NBA League Averages." Basketball-Reference.com - Basketball Statistics and History. https://www.basketball-reference.com/leagues/NBA_stats_totals.html.

12. Bucks post highest single-game field-goal percentage by any team in 21st century https://sports.yahoo.com/article/bucks-post-highest-single-game-040313061.html

13. https://www.statmuse.com/nba/ask/most-field-goals-made-record-in-a-game-nba-player

14. Lewis, G. J., & Stewart, N. (2003). The measurement of environmental performance: an application of Ashby’s law. Systems Research and Behavioral Science, 20(1), 31–52. https://doi.org/10.1002/sres.524

15. Norman, J., & Bar-Yam, Y. (2018). Special Operations Forces: A Global Immune System? In Springer Unifying Themes in Complex Systems IX (pp. 486–498). Springer International Publishing. https://doi.org/10.1007/978-3-319-96661-8_50

16. Norman, J., & Bar-Yam, Y. (2019). Special Operations Forces as a Global Immune System. In Springer Evolution, Development and Complexity (pp. 367–379). Springer International Publishing. https://doi.org/10.1007/978-3-030-00075-2_16

17. O’Grady, W., Morlidge, S., & Rouse, P. (2014). Management Control Systems: A Variety Engineering Perspective. SSRN Electronic Journal. https://doi.org/10.2139/ssrn.2351099

18. Love, T., & Cooper, T. (2007). Digital Eco-systems Pre-Design: Variety Analyses, System Viability and Tacit System Control Mechanisms. 2007 Inaugural IEEE-IES Digital EcoSystems and Technologies Conference, 452–457. https://doi.org/10.1109/dest.2007.372013

19. Love, T., & Cooper, T. (2007). Complex built‐environment design: four extensions to Ashby. Kybernetes, 36(9/10), 1422–1435. https://doi.org/10.1108/03684920710827391

20. Bushey, D. B., & Nissen, M. E. (1999). A Systematic Approach to Prioritizing Weapon System Requirements and Military Operations Through Requisite Variety. Defense Technical Information Center. https://doi.org/10.21236/ada371943

21. Jones, H. P. (2018). Evolutionary stakeholder discovery: requisite system sampling for co-creation.

22. Grimm, D. A. P., Gorman, J. C., Robinson, E., & Winner, J. (2022). Measuring Adaptive Team Coordination in an Enroute Care Training Scenario. Proceedings of the Human Factors and Ergonomics Society Annual Meeting, 66(1), 50–54. https://doi.org/10.1177/1071181322661074

23. Becker Bertoni, V., Abreu Saurin, T., & Sanson Fogliatto, F. (2022). Law of requisite variety in practice: Assessing the match between risk and actors’ contribution to resilient performance. Safety Science, 155, 105895. https://doi.org/10.1016/j.ssci.2022.105895

24. Tworek, K., Walecka-Jankowska, K., & Zgrzywa-Ziemak, A. (2019). Towards organisational simplexity — a simple structure in a complex environment. Engineering Management in Production and Services, 11(4), 43–53. https://doi.org/10.2478/emj-2019-0032

25. Chester, M. V., & Allenby, B. (2022). Infrastructure autopoiesis: requisite variety to engage complexity. Environmental Research: Infrastructure and Sustainability, 2(1), 012001. https://doi.org/10.1088/2634-4505/ac4b48

26. van der Hoek, M., Beerkens, M., & Groeneveld, S. (2021). Matching leadership to circumstances? A vignette study of leadership behavior adaptation in an ambiguous context. International Public Management Journal, 24(3), 394–417. https://doi.org/10.1080/10967494.2021.1887017

27. Ulrik, S., & Isabella, A. (2023). Variety versus speed: how variety in competence within teams may affect performance in a dynamic decision-making task.

28. Bakardzhiev, D., Vitanov, N.K. (2025). KEDE (KnowledgE Discovery Efficiency): A Measure for Quantification of the Productivity of Knowledge Workers. In: Georgiev, I., Kostadinov, H., Lilkova, E. (eds) Advanced Computing in Industrial Mathematics. BGSIAM 2022. Studies in Computational Intelligence, vol 641. Springer, Cham. https://doi.org/10.1007/978-3-031-76786-9_3

29. Heylighen, F., & Joslyn, C. (2001). Cybernetics and Second Order Cybernetics. In R. A. Meyers (Ed.), Encyclopedia of Physical Science and Technology, Eighteen-Volume Set, Third Edition (pp. 155-170). Academia Press. http://pespmc1.vub.ac.be/Papers/Cybernetics-EPST.pdf

30. Schwaninger, M., & Ott, S. (2024). What is variety engineering and why do we need it? Systems Research and Behavioral Science, 41(2), 235–246. https://doi.org/10.1002/sres.2964

31. AULIN‐AHMAVAARA, A.Y. (1979), "THE LAW OF REQUISITE HIERARCHY", Kybernetes, Vol. 8 No. 4, pp. 259-266. https://doi.org/10.1108/eb005528

32. Wu, T., Dufford, A. J., Mackie, M. A., Egan, L. J., & Fan, J. (2016). The Capacity of Cognitive Control Estimated from a Perceptual Decision Making Task. Scientific Reports, 6, 34025.

33. Abuhamdeh S (2020) Investigating the “Flow” Experience: Key Conceptual and OperationalIssues. Front. Psychol. 11:158.doi: 10.3389/fpsyg.2020.00158

34. Automatic Screw Tightening Machine and Its Hidden Features

35. Keating, C. B., Katina, P. F., Jaradat, R., Bradley, J. M., & Hodge, R. (2019). Framework for improving complex system performance. INCOSE International Symposium, 29(1), 1218-1232. https://doi.org/10.1002/j.2334-5837.2019.00664.x

36. S. Engell (1985). An information-theoretical approach to regulation.

37. K. Kijima, Y. Takahara, B. Nakano (1986). ALGEBRAIC FORMULATION OF RELATIONSHIP BETWEEN A GOAL SEEKING SYSTEM AND ITS ENVIRONMENT.

38. W. Kickert, J. Bertrand, J. Praagman (1978). Some Comments on Cybernetics and Control. IEEE Transactions on Systems, Man and Cybernetics.

39. S. Engell (1985). Information-theoretical bounds for regulation accuracy. IEEE Conference on Decision and Control.

40. Hui Zhang, Youxian Sun (2003). Bode integrals and laws of variety in linear control systems. Proceedings of the 2003 American Control Conference, 2003.

41. R. Conant (1969). The Information Transfer Required in Regulatory Processes. IEEE Transactions on Systems Science and Cybernetics.

42. S. Engell (1987). Analysis of Regulation Problems based on Real-Time Rate-Distortion Theory. American Control Conference.

43. Hui Zhang, Youxian Sun (2003). Information theoretic limit and bound of disturbance rejection in LTI systems: Shannon entropy and H/sub /spl infin// entropy. SMC'03 Conference Proceedings. 2003 IEEE International Conference on Systems, Man and Cybernetics. Conference Theme - System Security and Assurance (Cat. No.03CH37483).

44. N. C. Martins, M. Dahleh (2008). Feedback Control in the Presence of Noisy Channels: “Bode-Like” Fundamental Limitations of Performance. IEEE Transactions on Automatic Control.

45. Hui Zhang, Youxian Sun (2003). H/sub /spl infin// entropy and the law of requisite variety. 42nd IEEE International Conference on Decision and Control (IEEE Cat. No.03CH37475).

46. Tsuji, M., Crookshank, M., Olsen, M., Schemitsch, E. H., & Zdero, R. (2013). The biomechanical effect of artificial and human bone density on stopping and stripping torque during screw insertion. Journal of the mechanical behavior of biomedical materials, 22, 146–156. https://doi.org/10.1016/j.jmbbm.2013.03.006

47. Akizuki, K., & Ohashi, Y. (2015). Measurement of functional task difficulty during motor learning: What level of difficulty corresponds to the optimal challenge point?. Human movement science, 43, 107–117. https://doi.org/10.1016/j.humov.2015.07.007

48. Bootsma, J. M., Hortobágyi, T., Rothwell, J. C., & Caljouw, S. R. (2018). The Role of Task Difficulty in Learning a Visuomotor Skill. Medicine and science in sports and exercise, 50(9), 1842–1849. https://doi.org/10.1249/MSS.0000000000001635

49. Akizuki, K., & Ohashi, Y. (2013). Changes in practice schedule and functional task difficulty: a study using the probe reaction time technique. Journal of physical therapy science, 25(7), 827–831. https://doi.org/10.1589/jpts.25.827

50. Goldhammer, F.; Naumann, J.; Stelter, A.; Tóth, K.; Rölke, H.; Klieme, E.: The time on task effect in reading and problem solving is moderated by task difficulty and skill. Insights from a computer-based large-scale assessment - In: The Journal of educational psychology 106 (2014) 3, S. 608-626 - URN: urn:nbn:de:0111-pedocs-179679 - DOI: 10.25656/01:17967; 10.1037/a0034716

51. Boothroyd, G., and P. Dewhurst, "DESIGN FOR ASSEMBLY", Dept. of Mechanical Engineering, University of Massachusetts, Amherst, Massachusetts, 1983.

52. Jahin, A., Zidan, A. H., Bao, Y., Liang, S., Liu, T., & Zhang, W. (2025). Unveiling the mathematical reasoning in deepseek models: A comparative study of large language models. arXiv preprint arXiv:2503.10573.

53. FrontierMath: A Benchmark for Evaluating Advanced Mathematical Reasoning in AI

Getting started

Frequently Asked Questions

About KEDE and KEDEHub

KEDEHub Features

All we need to analyze the efficiency of your organization

Knowledge-Centric Metrics

The complete set of concepts, terms and theories

Need help?

KEDEHub Documentation

Knowledge Discovery Efficiency (KEDE) and Ashby's Law of Requisite Variety

Related Articles

Abstract

1. Introduction

2. The Law of Requisite Variety

Mathematical Formulation

Information-Theoretic Formulation

Residual Variety

3. Core challenges in applying Ashby's Law to real systems

Solution

4. Knowledge Discovery Process

Defining Knowledge to be Discovered

5. Quantifying Knowledge To Be Discovered

6. Generalizing KEDE

Anchoring KEDE to Natural Constraints

7. Applications

Tightening screws

Typing the longest English word

KEDE calculation

Measuring software development

Testing Intelligence

Basketball Game

Interpretation using Ashby’s Law

Applying the Model

Assembly Line

Speed of Light in Medium

Appendix

Is it correct that P(E=1)= R/D?

When it is roughly correct

When it's not exactly correct

Same applies to H(R)/H(D)

Conclusion

H(D|R) Dynamic Modeling Across Time

Example: Dynamic Modeling of H(D|R)`

Mathematical Representation

Conclusion

Selection as a Staged Process

How to cite:

Works Cited