Evaluating Rubik's Cube Solving Strategies
A Knowledge-Centric Perspective
Abstract
This article explores the intricacies of speedcubing, the competitive practice of solving Rubik's Cubes as quickly as possible.
To evaluate strategies for solving Rubik's Cube, we suggest adopting a Knowledge-centric Perspective. This means seeing knowledge as the fuel that drives the solving engine. Central to this perspective is the concept of the 'knowledge gap' - the difference between what a speedcuber knows and what they need to know to effectively solve the Rubik's Cube. This gap directly influences speedcuber's' work experience, talent utilization and productivity.
It introduces the application of KnowledgE Discovery Efficiency (KEDE) metric to quantify a speedcuber's proficiency by measuring the extent of their algorithmic knowledge and their efficiency in applying this knowledge to solve the cube.
KEDE evaluates the ratio of actual moves performed to the theoretical maximum number of moves in a given time, offering insights into the solver's understanding of various solving techniques.
By analyzing different solving approaches—ranging from standard methods involving basic algorithms to optimized strategies minimizing move counts— the article sheds light on how KEDE can serve as a powerful tool to assess and compare the effectiveness of speedcubing practices. Through this examination, the article contributes to a deeper understanding of the skills and strategies that define elite speedcubing performance.
KEDE definition
A Knowledge Discovery Process transforms invisible knowledge into visible, tangible output.
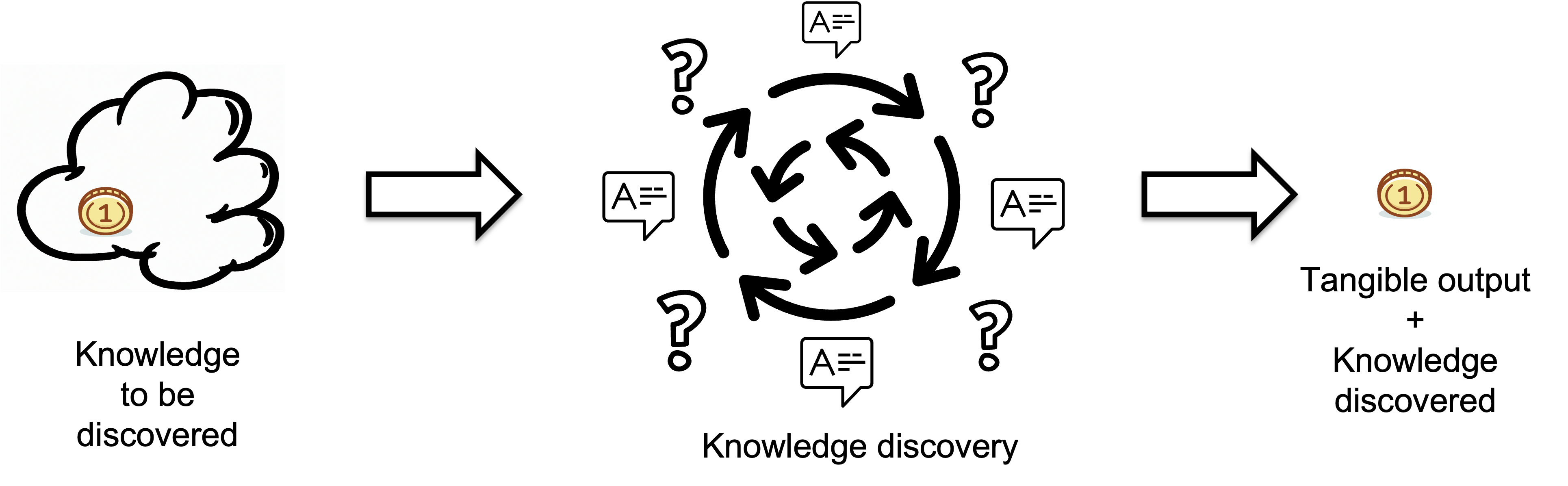
Think of it as a black box, which may contain senior and junior developers potentially using AI tools like ChatGPT. To learn more about it, please refer to this article.
To explain the tangible output, we can use an analogy from physics where a quantum is the smallest discrete unit of a physical phenomenon. In software development, tangible output comprises symbols produced..The quality of the output is assumed to meet target standards.
Inputs represent the knowledge developers lack before starting a task i.e. the missing information or knowledge that needs to be discovered, which is measured in bits.
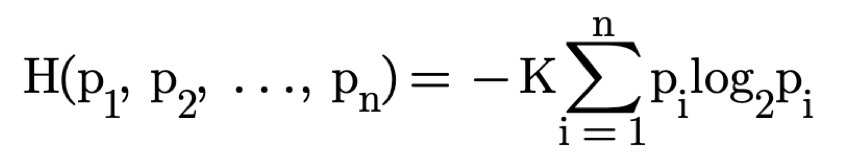
To quantify the knowledge developers didn't have before starting a task, we introduce a new metric called KEDE (KnowledgE Discovery Efficiency).
(1)
KEDE is a measure of how much of the required knowledge for completing tasks is covered by the prior knowledge. KEDE quantifies the knowledge software developers didn't have prior to starting a task, since it is this lack of knowledge that significantly impacts the time and effort required. KEDE is inversely proportional to the missing information required to effectively complete a task, and has values in the closed interval (0,1]. The higher the KEDE the less knowledge to be discovered.
Solving a Rubik's Cube
The knowledge perspective applies to all human activities where learning and applying knowledge are essential to produce a tangible result. Like solving the Rubik’s Cube! People who compete at solving a Rubik’s Cube as fast as possible are called speedcubers. The fastest time to solve a 3x3x3 rotating puzzle cube is 3.13 seconds by Max Park (USA) at the Pride in Long Beach 2023 event on 11 June 2023.
The time it takes to solve a Rubik's Cube is related to the raw number of moves (also known as "move count") required to solve the cube and how quickly and efficiently those moves can be performed. A single move is typically counted when a face of the cube makes a 90-degree turn.
Speedcubers do not always aim for the minimum number of moves because solving in the fewest possible moves and solving as quickly as possible are different challenges. For instance, if those 20 moves take 1 hour then that will not be fast.
Speedcubers use algorithms and solving methods designed to balance a low move count with the speed at which those moves can be executed. Techniques like CFOP (Cross, F2L, OLL, PLL), Roux, and ZZ are designed to be both efficient in terms of moves and conducive to fast execution.The emphasis is on the execution speed of an algorithm sequence that the cuber has memorized and practiced extensively. World record solves involve a combination of a highly efficient solving method, a favorable scramble that may require fewer moves than average to solve, and the skillful, rapid execution of moves.
The execution speed of moves is typically measured in Turns per Second (TPS). TPS is a measure of the cuber's physical execution speed, capturing how quickly they can perform turns, regardless of whether those turns are quarter (90-degree) or half (180-degree) turns The calculation of TPS is based on the total number of moves executed divided by the total time taken to complete the solve, giving a rate of moves per second that reflects the cuber's speed.
For top-level speedcubers, the TPS can range from 5 to over 12 during a solve, depending on the phase of the solve and the specific techniques being used. This metric includes pauses for thinking and deciding on the next moves, and the actual time for executing the physical action.
Efficient move selection and aiming for a minimal total move count do reflect a deeper knowledge of solving algorithms and a thorough understanding of the Rubik's Cube's mechanics.
This time spent thinking could be for various reasons, including:
- Algorithm Efficiency: Knowledge of a wide range of efficient algorithms enables a solver to select the optimal moves for any given situation. Familiarity with these algorithms means the solver can execute them quickly, with little to no hesitation.
- Pattern Recognition: Identifying the current state of the cube and determining the most efficient algorithm or sequence of moves to apply next. More time spent in recognition suggests a need for further familiarization with patterns and their corresponding solutions.
- Look-Ahead: Trying to foresee the next cube state and prepare the next moves while executing the current ones. Difficulty with look-ahead can lead to pauses between algorithms as the solver assesses the cube.
- Strategic Planning: A deep understanding of the cube also allows for strategic planning, where solvers might choose a slightly longer algorithm that transitions more smoothly into subsequent steps, thus maintaining a high TPS and reducing overall solve time.
- Decision-Making: Choosing between multiple known algorithms for a particular situation, especially if certain solutions might be more efficient in terms of move count but less familiar or slightly slower to execute.
- Execution Hesitation: Even with a clear understanding of the next moves, a solver might momentarily hesitate to ensure accurate execution, especially with complex or less-practiced algorithms.
- Error Correction: Pausing to correct mistakes or to reorient the cube if the solver loses track of their plan during execution.
Early stages of a solve, like building the cross in the CFOP method, might have a lower TPS due to the need for inspection and decision-making. In contrast, later stages, such as the OLL (Orientation of the Last Layer) and PLL (Permutation of the Last Layer), can have a very high TPS because the moves are more reflexive and based on memorized algorithms.
Turns per second (TPS) in speedcubing depends on a combination of physical training and the knowledge of algorithms. Here's how these factors contribute:
- Physical Training: This involves developing the dexterity, speed, and precision required to execute cube rotations quickly. Speedcubers often practice specific drills to improve their finger tricks (the techniques used to turn the cube's faces with minimal finger movement), hand positioning, and overall agility. Such physical training helps reduce the time it takes to perform each move, allowing for faster solves. Consistent practice is essential for muscle memory development, enabling cubers to perform turns rapidly without having to consciously think about each movement.
- Knowledge of Algorithms: Knowing a wide array of algorithms allows speedcubers to solve the cube more efficiently. This knowledge includes not just the steps for solving the cube from any given state but also recognizing patterns and situations quickly and knowing the best algorithm to apply in each case. Advanced speedcubers memorize hundreds of algorithms for various cube states, especially for the last layer, to minimize the number of moves required to complete the solve. The faster a cuber can recognize the cube's state and recall the corresponding algorithm, the less time they spend pausing between sequences of moves, thus increasing their TPS.
Both aspects are critical for achieving high TPS rates. Physical training without a deep understanding of algorithms may lead to fast but inefficient solves, while extensive knowledge of algorithms without the ability to quickly execute them physically limits the solver's speed. The most successful speedcubers combine both elements, continuously refining their physical techniques and expanding their algorithmic knowledge to optimize their performance.
The highest TPS rates are achieved when a speedcuber spends minimal to no time thinking about the next move because they instantly recognize the pattern and know exactly which algorithm to apply. In these scenarios, the cognitive load is minimized, allowing the cuber to focus entirely on the physical aspect of turning the cube.
In high-speed solving, a single cube rotation can be executed incredibly quickly, often in a fraction of a second. For a rough estimate, consider that top speedcubers can achieve TPS (turns per second) rates of 5 to over 12 during various phases of their solves. If we consider a TPS rate of 12 as an example of a high rate achieved when ignoring the cognitive aspect of deciding which move to make, then the time to execute a single turn would indeed be 1/12th of a second, or approximately 0.083 seconds. This calculation is a simple way to understand the speed at which top speedcubers can operate when they are in a flow state, executing moves they have extensively practiced and memorized.
This scenario typically occurs during the latter stages of a solve, such as during specific algorithm sequences for the OLL (Orientation of the Last Layer) and PLL (Permutation of the Last Layer) steps in methods like CFOP, where the sequences are memorized and can be executed rapidly without hesitation.
It's important to note that achieving and maintaining a TPS of 12 throughout an entire solve is extremely challenging and would be considered exceptional even among the best speedcubers. Most solvers will have varying TPS rates throughout a solve, with peaks during certain algorithm executions and lower rates at other times due to decision-making or transition between different steps of the solve.
Calculating KEDE
If we use a TPS of 12 as a benchmark for the best possible speed at which moves are executed without pause for thought, then achieving a lower TPS over the course of a solve would indeed suggest that the solver spent some amount of time thinking or deciding on their moves.
Thus, the time it takes a speedcuber to solve a Rubik's Cube can provide insight into their level of knowledge about algorithms and patterns, as well as their skill in applying this knowledge efficiently during a solve.
To quantify these insights, we introduce the KnowledgE Discovery Efficiency (KEDE) metric[2]. KEDE evaluates the extent to which a solver's pre-existing knowledge covers the necessary algorithms and techniques for solving tasks. As a versatile metric applicable across various knowledge discovery processes, KEDE must be tailored to each specific context.
For Rubik’s Cube solving, we adapt KEDE as follows:
- Let r represent the maximum achievable Turns Per Second (TPS).
- During a time interval T, the theoretical maximum number of moves, N, equals T×r.
- The actual number of moves performed in interval T is denoted as S.
Therefore, we calculate KEDE using the formula:
Assuming r=12 moves/second and T=1 hour (or 3600 seconds) then N=43200, leading to:
Consider three distinct approaches to solving the Rubik's Cube:
- Standard Approach:: Utilizes numerous iterations of basic algorithms (100 moves).
- Optimized Approach: Employs a specific, efficient method to minimize moves (20 moves)
- Aimless Random Approach: Involves an indeterminate number of moves.
By labeling the move counts for these approaches as: S_standard, S_optimized, S_aimless.we can calculate a KEDE score for each.
This allows us to objectively measure a cuber's knowledge level by the number of moves they execute per hour of continuous Rubik’s Cube solving.
How to cite:
Bakardzhiev D.V. (2024) Evaluating Rubik's Cube Solving Strategies: A Knowledge-Centric Perspective https://docs.kedehub.io/kede/kede-rubik.html
Works Cited
1. Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal. 1948;27(3):379-423. doi:10.1002/j.1538-7305.1948.tb01338.x
2. Bakardzhiev, D., Vitanov, N.K. (2025). KEDE (KnowledgE Discovery Efficiency): A Measure for Quantification of the Productivity of Knowledge Workers. In: Georgiev, I., Kostadinov, H., Lilkova, E. (eds) Advanced Computing in Industrial Mathematics. BGSIAM 2022. Studies in Computational Intelligence, vol 641. Springer, Cham. https://doi.org/10.1007/978-3-031-76786-9_3
5. Zheng, J., & Meister, M. (2024). The unbearable slowness of being: Why do we live at 10 bits/s?. Neuron.
4. Purdue ECE students shatter Guinness World Record for fastest puzzle cube-solving robot https://engineering.purdue.edu/ECE/News/2025/purdue-ece-students-shatter-guinness-world-record-for-fastest-puzzle-cube-solving-robot
Getting started


