Knowledge Discovery Efficiency (KEDE) and Ashby's Law of Requisite Variety

Abstract

We address Real-world applications of Ashby's Law by adopting Ashby's strict black-box perspective: only external behaviour is observable. First we define the multi-staged selection process of narrowing down and selecting the appropriate response from the set of alternative responses as the Knowledge Discovery Process. We then establish H(X|Y) as the knowledge to be discovered, which is the gap in internal variety that had to be compensated by selection. This quantifies how much disorder the regulator still permits and, conversely, how close the system comes to meeting Ashby's requisite-variety condition. In information-theoretic terms, perfect regulation requires H(X|Y) = 0. Then we quantify the knowledge to be discovered H(X|Y) based on the observable outcomes. Building on this result, we generalize Knowledge-Discovery Efficiency (KEDE) - scalar metric that quantifies how efficiently a system closes the gap between the variety demanded by its environment and the variety embodied in its prior knowledge. KEDE operationalises requisite variety when internal mechanisms remain opaque, offering a diagnostic tool for evaluating whether biological, artificial, or organisational systems absorb environmental complexity at a rate sufficient for effective regulation. Finally we present applications of KEDE in diverse domains, including typing the longest English word, measuring software development, testing intelligence, basketball game, assembling furniture, and speed of light in medium.

Introduction

The Law of Requisite Variety, formulated by W. Ross Ashby, states that for a system to effectively regulate its environment, it must have at least as much variety/complexity as its environment[1]. This principle is foundational in disciplines such as cybernetics, control theory, and machine learning.

The concept of requisite variety has since been applied across diverse domains, including organizational theory, ecology, and information systems. It underscores the necessity for systems to adapt to environmental complexity in order to maintain stability and achieve intended outcomes.

Real-world attempts to apply Ashby's Law of Requisite Variety face three persistent obstacles. (i) Combinatorial explosion: enumerating all relevant states of a system and its environment quickly becomes intractable, especially when hidden or unmeasured variables are present. (ii) Dual control dilemma: a regulator must simultaneously amplify its own control variety and attenuate external variety—an optimization that is delicate in multiscale, hierarchical, and time-varying settings such as digital ecosystems or military command structures. (iii) Resource constraints: limited data, computational power, and organisational capacity often preclude sophisticated control architectures. Existing remedies—markup-language state catalogues, iterative multidimensional sampling, and distributed self-organising controllers—mitigate but do not eliminate these limitations.

In section 2, we conduct a literature review of the primary challenges in applying Ashby's Law to real-world systems and propose a black-box solution: treating the system as a black box, observing the probability of successful outcomes to disturbances, and estimating the gap in its internal variety from that. In section 3, we present the Law of Requisite Variety in both its set-based formulation—covering the Table of Outcomes, requisite variety, goal revision, and behavioral rework—and its information-theoretic formulation, covering entropy, probabilistic success, residual variety bounds, response-equivalence, and the regulator's learned law of action. We conclude section 3 by introducing Knowledge To Be Discovered as the conditional entropy H(X|Y) that remains after available disturbance information is known. In section 4, we establish the Knowledge Discovery Process as the staged reduction of Knowledge To Be Discovered. We develop this in three layers: a set-based formulation of staged selection covering episodes, closures, and rule regulation; an information-theoretic formulation introducing the expected staged reduction of H(X|Y), action units, and response-class commitment; and learning across episodes, including comparable episodes, the learning axiom, and the posterior-becomes-prior rule. We also develop the operational ledger and the knowledge ledger, together with their window-level accounting measures and a three-loop feedback reading of all revisions. In section 5, we show how to quantify Knowledge To Be Discovered from observable outcomes alone, deriving the operational one-bit effective-depth estimator. and its relationship to the latent entropy. In section 6, we generalize the Knowledge-Discovery Efficiency (KEDE)—a scalar metric in [0,1] that quantifies how efficiently a system closes the gap between the variety demanded by its environment and the variety embodied in its prior knowledge. Finally, in section 7, we explore applications of KEDE across diverse domains including manual assembly, typing, software development, intelligence testing, sports performance, industrial assembly lines, and the speed of light in a medium, demonstrating its utility as a unified diagnostic tool for evaluating system performance and adaptability.

Core challenges in applying Ashby's Law to real systems

We conducted a literature review aimed at identifying the primary challenges and limitations associated with applying Ashby's Law in real-world systems.

A central challenge that emerges is the measurement of variety. In most of the reviewed literature, the concept of variety is either poorly defined or not explicitly measured, resulting in ambiguity and potential misinterpretation of the law's implications. Key obstacles to effective measurement include:

The direct measurement of variety is fundamentally incomputable for all but the simplest systems [14].
Hidden variables introduce uncertainty and complicate measurement efforts [15].
Trade-offs often arise between variety at different scales [16].
A combinatorial explosion occurs when attempting to enumerate all possible system states [15,16].
Resource limitations constrain the feasibility of comprehensive measurement [20].
Environmental complexity is frequently “unknowable,” preventing complete assessment [25].
Most studies lack explicit or standardized methods for quantifying variety [14,17'-20,25,27].
Existing approaches often lack rigorous quantitative validation [17].

Several measurement methods have been proposed, including:

Markup language-based variety estimation [18],
Iterative sampling techniques [21],
Entropy and determinism metrics to evaluate communication complexity, where greater variety was correlated with improved effectiveness [22],
Social network and cluster analysis to assess resilience [23], and
Multiple Correspondence Analysis (MCA) for capturing organizational complexity [24].

In addition, a subset of studies estimate variety through observed performance rather than structural attributes. Notable examples include:

Communication-based performance measures, employing determinism metrics to evaluate repeatable patterns in team behavior [22];
Team performance assessments, using task-based surveys to evaluate an organization's risk-handling capabilities [23];
Leadership behavior analysis, based on actual behavioral responses to simulated scenarios [26]; and
Relative performance comparisons, assessing organizational effectiveness across contexts using perception-based rather than absolute metrics [14].

While these performance-based approaches provide practical insights, they often rely on subjective or indirect indicators of variety, which may introduce biases and limit their generalizability. For example, performance outcomes may fail to account for hidden variables or the underlying complexity of the system [15]. Moreover, these approaches remain underrepresented in the literature, where structural and theoretical analyses still dominate.

In summary, although numerous methods for measuring variety have been proposed, no single comprehensive or universally accepted solution has emerged. Quantification remains a persistent challenge in the application of Ashby's Law to complex real-world systems.

Solution

These challenges significantly hinder the practical application of Ashby's Law. Whether considering a human, an AI model, or an organization, we are typically limited to observing external behavior rather than internal mechanisms—unless we are able to "open the box."

Ashby himself emphasized that all real systems can be considered black boxes. He argued that while black boxes mimic the behavior of real objects, in practice, real objects are black boxes: we have always interacted with systems whose internal workings are, to some extent, unknown.

This leads to what Ashby termed the black box identification approach [2], which involves:

Perturbing the system by applying external disturbances,
Measuring the system's responses to these perturbations, and
Inferring the internal variety or capacity from the observed input-outcome relationships.

In most practical scenarios, we are only able to observe the outcomes of a system. These observable outcomes can be used to infer bounds on the system's internal variety—specifically, the extent of variety it must possess or lack in order to exhibit the observed behavior.

We propose such an approach: to treat the system as a black box, observe the probability of successful outcomes to disturbances, and estimate the gap in its internal variety based on that. Let E denote the event that the system gives an response to disturbance D, and let R be the regulator's action. In information-theoretic terms, perfect regulation requires H(R|D) = 0[31]. Using our novel information-theoretic estimator, empirical estimates of P(E=1) are used to quantify H(R|D) in bits of information. This quantifies how much disorder the regulator still permits and, conversely, how close the system comes to meeting Ashby's requisite-variety condition.

The Law of Requisite Variety

For a system to effectively regulate its environment, it must have at least as much variety as its environment.

Set-based formulation

Regulation achieves a goal by selecting responses against disturbances.

$E = (E_{1}, \dots, E_{n})$ is the essential-variable vector. The essential variables $E_{1}, \dots, E_{n}$ are the goal-relevant state components. $E_{i}$ is the value set of $E_{i}$ . The essential variables define the dimensions; their value sets define the coordinate domains of the essential-variable space $E = E_{1} \times E_{2} \times ... \times E_{n}$ , which is the set of all possible combinations of their values[29].

An essential state $e \in E$ is one particular point in the essential-variable space, i.e. a tuple of values of these dimensions, e.g. $e = (36.8 ° C, 92 mg / dL, \dots)$ .

It is assumed that the goal has already been determined: the acceptable essential states are given by an acceptable region $η \subseteq E$ in the essential-variable space. Thus, the goal is a region in a multidimensional essential-variable space $E$ .

Let D, R, and Z denote, respectively, the disturbance variable, regulatory-response variable, and outcome variable. Let their corresponding sets of possible values be $D$ , $R$ , and $Z$ . Thus $d \in D$ , $r \in R$ , and $z \in Z$ are particular values.

In the general case, the outcome-value space may itself be multidimensional. Let $Z = (Z_{1}, \dots, Z_{m})$ be the outcome-variable vector. The outcome variables $Z_{1}, \dots, Z_{m}$ are the components used to describe the concrete or functional result produced by a disturbance-response pair. $Z_{j}$ is the value set of $Z_{j}$ . Thus the outcome-value space is $Z = Z_{1} \times Z_{2} \times ... \times Z_{m}$ .

An outcome-value $z \in Z$ is one particular point in the outcome-value space. In the multidimensional case, it has the form $z = (z_{1}, \dots, z_{m})$ . In the Appendix we have an example of a typing task, where an outcome-value may record both the intended target position and the typed symbol: $z = (p, a)$ .

The number of outcome dimensions m need not equal the number of essential-variable dimensions n. The outcome-value space $Z$ describes the result produced by the system, while the essential-variable space $E$ describes the goal-relevant state used to judge that result. The mapping from outcomes to essential-variable values will be introduced below.

The scalar outcome-value case is recovered when $m = 1$ . In that special case, each outcome-value may be treated as an unstructured value. More generally, each table cell still contains one outcome-value, but that outcome-value may itself be internally structured as a tuple.

We use roman $E$ for the essential-variable vector and script $E$ for its value space. Likewise, we use roman $Z$ for the outcome-variable vector and script $Z$ for its value space.

The Table of Outcomes is the map

T : D \times R \to Z

so that for each disturbance-value $d$ and response-value $r$ , the value $T (d, r)$ is the outcome-value $z \in Z$ .

Thus the table T is two-dimensional in its indexing by disturbance-response pairs (d,r), while each cell-entry may be a scalar outcome-value or a structured outcome-vector. The scalar-outcome case is recovered when $Z = Z_{1}$ .

T		R
T		r₁	r₂	r₃	...
D	d₁	z₁₁	z₁₂	z₁₃	...
	d₂	z₂₁	z₂₂	z₂₃	...
	d₃	z₃₁	z₃₂	z₃₃	...
	d₄	z₄₁	z₄₂	z₄₃	...
	...	...	...	...	...

Two distinct disturbance-response pairs may yield the same outcome-value:

T (d_{1}, r_{1}) = T (d_{2}, r_{2}) = z

This means that repetition belongs to the mapping T, not to the set $Z$ . A set contains each of its elements only once. So one should not say that $Z$ contains repeated values. What repeats is the same outcome-value appearing as the image of multiple table-cells.

Correspondence between outcome-values and essential-variable values. The “outcomes” in the Table of Outcomes are simple outcome-values, without any implication of desirability. An outcome-value $z \in Z$ is a concrete or functional result of a disturbance-response pair. An essential-variable value $e \in E$ is the goal-relevant state description used to judge whether the result falls inside or outside the acceptable region.

The correspondence between outcome-values and essential-variable values is therefore not automatic. It is part of the modeling frame of the regulatory problem. To use a function from outcomes to essential-variable values, the outcome-description must be specified at a level of detail sufficient to determine the relevant essential-variable value. In this article we assume that this has been done. Thus each outcome-value under the adopted description has a determinate associated essential-variable value.

φ : Z \to E

so that $φ (z) = e$ . This means that the function $φ$ is a modeling map from the outcome-description used in the table to the essential-variable description used for regulation. It should not be read as saying that every possible description of an outcome would automatically determine an essential-variable value. If the outcome-description were too coarse to determine the relevant essential-variable value, then $φ$ would have to be replaced by a relation, a refinement of $Z$ , or a probabilistic mapping.

The reduced, bijective, and many-to-one cases discussed below are therefore not alternatives to this modeling assumption. They are different ways in which the adopted outcome-description may correspond to the essential-variable description. In the reduced case, outcome-values already are essential-variable values. In the bijective case, outcome-values and essential-variable values are distinct descriptions but correspond one-for-one. In the many-to-one case, several finer-grained outcome-values correspond to the same essential-variable value.

Reduced correspondence. The special case is the reduced representation in which the table T directly contains values of the essential variables, i.e.

Z = E and φ = {id}_{E}

so that the table entries are already values of the essential variables.[1] More generally, however, φ may be bijective or many-to-one, depending on the level of description adopted.

Bijective correspondence between outcome-values and essential-variable values. This is the case in which each relevant outcome-value maps to a unique essential-variable value, and each relevant essential-variable value is represented by exactly one outcome-value. In the bijective case, $φ$ is one-to-one and onto between the relevant outcome-values and the relevant essential-variable values represented in the regulatory model, not bijective over the entire possible outcome and essential-variable spaces. Then $Z$ and $E$ are conceptually distinct but informationally equivalent: $φ : Z \to E$ with $z_{1} \neq z_{2} \to φ (z_{1}) \neq φ (z_{2})$ and every essential-variable value relevant to the regulatory model $e \in E$ has exactly one corresponding $z \in Z$ . On this reading, $Z$ may still be understood as the outcome-value space and $E$ as the essential-variable space, but every relevant distinction in outcomes is mirrored one-for-one at the level of the essential variables. This is the form used in later reformulations such as $D \to R \to Y \leftrightarrow E$ with an explicit bijection between the outcome-value variable and the essential variable E. In that literature Y corresponds to our outcome variable Z, or to the induced outcome variable generated through T. Aulin-Ahmavaara's formulation uses a one-to-one mapping between outcome Y and essential variable E, so our $φ : Z \to E$ is a generalization of that case[31]. See the illustrative example in the Appendix.

Many-to-one correspondence between outcome-values and essential-variable values. This is the case in which multiple distinct outcome-values map to the same essential-variable value. Ashby says that a particular outcome can be treated “as unit with unit,” but “in another context, [it] may be analysed more finely.[1]” That means an outcome can be used as a single table-entry in the regulatory schema, even though in a more detailed analysis it may unfold into a whole trajectory, microstate, or process.[1] Then different outcome-values can collapse to the same essential-variable value: $z_{1} \neq z_{2} \land φ (z_{1}) = φ (z_{2}) = e$ .

On this reading, $Z$ contains finer-grained outcomes, while $E$ contains the coarser essential-variable values that matter for survival or goal-attainment. The many-to-one relation therefore expresses that several distinct outcome-states may be equivalent from the standpoint of regulation. Successful regulation is still judged at the level of the essential variables: distinct trajectory histories may all count as equally successful if they yield the same relevant value of $E$ and hence fall within the acceptable region $η \subseteq E$ . This is a refinement of Ashby's basic regulatory schema, but it is an added modeling layer[1]. See the illustrative example in the Appendix.

In this article formulas below are written in the general $φ : Z \to E$ form. Most later calculations use the general $φ$ -form; where individual outcome deletion/addition is interpreted literally, the reduced or bijective case is assumed unless stated otherwise.

Requisite variety

The regulator does not choose outcome-values directly. It selects a response-value in the presence of a disturbance-value, and thereby determines an outcome-value.

Strictly speaking, there may be many disturbance-values that are conceivable in the world but not part of the regulatory problem currently being modeled. Let $D_{all}$ denote the larger set of all conceivable disturbance-values. In the present formulation, however, we restrict attention to the disturbance-values under consideration in the regulatory problem. For notational economy, we write this context-restricted disturbance set simply as $D$ , where $D \subseteq D_{all}$ .

This restriction is part of the modeling frame, not an effect of regulation. It does not mean that the regulator has already reduced the disturbance variety. It means only that success is being evaluated over the disturbance-values included in the present regulatory problem. Thus, from this point onward, $D$ means the disturbance set under consideration.

In Ashby's table formulation, the “actual outcomes” is the rule-induced actual outcome-set selected from the possible outcome table by the regulator's response choices. They are actual in contrast to the full set of possible outcomes $Z$ , not necessarily actual in the narrower historical sense of having occurred in a single observed run[1][8].

Let the regulator use a response rule

ρ : D \to R

This induces the actual outcome map

y_{ρ} : D \to Z, y_{ρ} (d) := T (d, ρ (d))

and its image:

y_{ρ} [D] = {y_{ρ} (d) : d \in D} \subseteq Z

The image $y_{ρ} [D]$ is the rule-induced actual outcome-set under the response rule $ρ$ . It contains the outcome-values selected from the possible outcome table when each disturbance-value under consideration is paired with the response chosen for it by the rule $ρ$ . In this Ashby-style sense, these are the rule-induced actual outcomes: actual relative to the regulator's response rule, as distinct from the full space of possible outcomes $Z$ .

This should be distinguished from the historically realized outcome-set in one particular run. If only some disturbance-values actually occur, let $D_{r} \subseteq D$ be the historically realized disturbance subset. Then the historically realized outcome-set is

O_{ρ}^{r} := y_{ρ} [D_{r}] \subseteq y_{ρ} [D] \subseteq Z .

Thus $Z$ is the possible outcome-value space; $y_{ρ} [D]$ is the actual outcome-set over the modeled disturbance domain; and $O_{ρ}^{r}$ is the historically realized outcome-set in the actual case.

Successful regulation requires that the essential-variable values corresponding to all rule-induced actual outcomes $y_{ρ} [D]$ lie in the acceptable region: $φ [y_{ρ} [D]] \subseteq η$ for any $A \subseteq Z, φ^{} [A] := {φ^{} (z) : z \in A} .$

This is a universal rule-level success condition over the disturbance set under consideration. At a particular moment only one disturbance may occur, but the response rule is judged by what it would produce for every disturbance in the modeled set.

This set-based representation tracks which outcome-values can occur under the policy, but it does not track multiplicity, frequency, or probability. Its role here is to support a universal success condition over the disturbance set.

Equivalently, successful regulation requires that every disturbance-value under consideration be mapped, through the selected response rule, into an acceptable outcome-value:

y_{ρ} [D] \subseteq φ^{- 1} [η]

Here, the acceptable outcome-set $φ^{- 1} [η]$ denotes the preimage of the set $η$ , not a two-sided inverse function. Also $φ^{- 1} [η]$ is a subset of $Z$ , so it is at the outcome-value level.

This subset relation is the primary success condition. It says that every actual outcome produced under the response rule $ρ$ must lie in the acceptable outcome-set. Any variety inequality derived from it is only a necessary numerical consequence, not the defining criterion of success. In Ashby-style terms, regulation succeeds when the rule-induced actual outcomes remain within the goal subset[1].

In this subsection, V denotes count-variety: for any finite set $A$ , we define $V (A) := | A |$ , the number of distinguishable values/states in $A$ under the adopted classification. The following count-variety statements assume that the relevant spaces have been discretized into distinguishable classes under the adopted modeling resolution. If $η$ is an interval in a continuous space, plain cardinality becomes unhelpful because many regions may have the same infinite cardinality. For continuous spaces, the same role would have to be played by a measure, entropy, or another explicitly chosen variety measure. Thus all formulas written with $V$ are cardinality statements. Therefore, at the level of variety, success implies the following necessary numerical bound:

V (φ [y_{ρ} [D]]) \leq V (η)

Similarly, from $y_{ρ} [D] \subseteq φ^{- 1} [η]$ we obtain the necessary bound

V (y_{ρ} [D]) \leq V (φ^{- 1} [η])

These variety inequalities are consequences of the subset condition. They are not, by themselves, equivalent to it: an actual outcome-set $y_{ρ} [D]$ may have variety no greater than that of an acceptable set and still fail to be a subset of that set. So success is fundamentally a matter of set inclusion, while the variety inequalities are derived necessary conditions. They are not, by themselves, equivalent to it.

Under the reduced representation in which $Z = E$ and $φ = {id}_{E}$ , the outcome-values are already values of the essential variables, so the success condition reduces to

y_{ρ} [D] \subseteq η

and therefore implies the numerical bound

V (y_{ρ} [D]) \leq V (η)

This numerical compatibility condition is still only necessary, not sufficient. The decisive success criterion remains: $φ [y_{ρ} [D]] \subseteq η$ .

Thus, in this set-based formulation, regulatory success is stated at the level of the rule-induced actual outcome-set $y_{ρ} [D]$ , not at the level of a single actual outcome $z_{t}$ which is used to state success at a particular time.

A special finite-table lower-bound result. Under Ashby's finite table T idealization, a special count-variety consequence of the law of requisite variety can be stated precisely[1][8]. Suppose the table T has finitely many disturbance-values and response-values, and suppose that no response-column contains a repeated outcome-value. Equivalently, for every fixed response-value $r \in R$ , the map $d \mapsto T (d, r)$ is injective. Thus a single unchanged response-value cannot by itself collapse different disturbance-values into the same outcome-value.

Let the regulator select one response-value for each disturbance-value by a response rule $ρ : D \to R$ . This selects one cell from each disturbance-row of the table and induces the actual outcome-set

y_{ρ} [D] = {T (d, ρ (d)) : d \in D} \subseteq Z .

The response rule may use only a subset of the available response repertoire. Define the used response-set as

R_{ρ} := ρ [D] \subseteq R .

Because no response-column contains a repeated outcome-value, any one outcome-value can appear among the selected cells at most once per used response-column. Since the rule uses $V (R_{ρ})$ response-columns, any one outcome-value can cover at most $V (R_{ρ})$ selected disturbance-rows. But the response rule selects one cell from each of the $V (D)$ disturbance-rows. Assume $D$ is non-empty, so that $R_{ρ}$ is also finite and non-empty. Therefore the selected cells cannot collapse into fewer than the ceiling of disturbance-rows divided by used response-columns:

V (y_{ρ} [D]) \geq ⌈ \frac{V (D)}{V (R_{ρ})} ⌉ .

Since $R_{ρ} \subseteq R$ , we also have $V (R_{ρ}) \leq V (R)$ . Therefore the weaker repertoire-level lower bound is:

V (y_{ρ} [D]) \geq ⌈ \frac{V (D)}{V (R)} ⌉ .

This is a finite-table, count-variety quotient analogue of the Ashby-style requisite-variety bound. It is not Ashby’s general entropy formulation. It is not derived from the goal-subset condition alone. It follows from the additional table assumption that no response-column already contains repeated outcome-values. If the table itself contains such repetitions, then some disturbance variety has already been collapsed by the table structure before the regulator's response rule is considered. In that case this quotient lower bound need not hold at the outcome-value level.

This is an outcome-value-level bound before applying $φ$ . In the many-to-one case, $φ$ may collapse several distinct outcome-values into one essential-variable value, so the same lower bound need not hold for $V (φ [y_{ρ} [D]])$ unless $φ$ is injective on the selected outcome-values.

The quotient bound is a lower bound on the variety of the actual outcome-set selected by the response rule. Successful regulation, however, is still defined by set inclusion, not by the quotient alone. The success condition remains:

y_{ρ} [D] \subseteq φ^{- 1} [η] .

Therefore a necessary outcome-level numerical compatibility condition for success is:

⌈ \frac{V (D)}{V (R)} ⌉ \leq V (φ^{- 1} [η]) .

This condition is necessary, not sufficient. It says only that the acceptable outcome-set is numerically large enough to contain the unavoidable residual outcome variety. It does not guarantee that the table entries are arranged so that some response rule actually maps every disturbance-value into the acceptable outcome-set. Success remains a matter of the subset relation itself.

If one wants the numerical condition to count only outcome-values that are actually attainable from the table, define the table-image as

Im (T) := {T (d, r) : d \in D, r \in R} \subseteq Z .

Then the attainable acceptable outcome-set is

O_{acc}^{att} := Im (T) \cap φ^{- 1} [η] .

Using this stricter attainable set gives the sharper necessary condition:

⌈ \frac{V (D)}{V (R)} ⌉ \leq V (O_{acc}^{att}) .

In the reduced representation, where $Z = E$ and $φ = {id}_{E}$ , the acceptable outcome-set is just the acceptable essential-variable region:

φ^{- 1} [η] = η .

Therefore the necessary numerical condition becomes:

⌈ \frac{V (D)}{V (R)} ⌉ \leq V (η) .

The same reduction holds in the bijective case, provided $φ$ preserves cardinality on the relevant acceptable sets. In the many-to-one case, however, $V (φ^{- 1} [η])$ may be much larger than $V (η)$ . Thus the outcome-level compatibility condition and the essential-variable-level compatibility condition coincide in the reduced or bijective case, but can diverge in the many-to-one case.

Outcome map induced by a response rule at time t

At time $t$ , let the regulator use the response rule

ρ_{t} : D \to R

The induced actual outcome map is

y_{t} : D \to Z, y_{t} (d) := T (d, ρ_{t} (d))

where $y_{t}$ := $y_{ρ_{t}}$ for notational economy.

The acceptable outcome-set at time t is not chosen directly in $Z$ ; it is induced by pulling back the acceptable essential-variable region $η_{t} \subseteq E$ along the outcome-to-essential-variable map $φ$ .

O_{acc, t} := φ^{- 1} [η_{t}] = {z \in Z : φ (z) \in η_{t}}

Thus the acceptable outcome-set is the pullback, or preimage, of the acceptable essential-variable region. An outcome-value is acceptable at time t exactly when its associated essential-variable value lies in $η_{t}$ .

Successful regulation under the criterion prevailing at time $t$ means that the response rule $ρ_{t}$ maps every disturbance under consideration into the acceptable outcome-set for that time:

y_{t} [D] \subseteq O_{acc, t}

Equivalently,

φ [y_{t} [D]] \subseteq η_{t}

Goal revision with fixed table and time-indexed acceptable outcomes

We consider a regulator acting against disturbances within a fixed system structure. The aim is to model the case in which the structure of the system does not change from time t₁ to time t₂, but the criterion of success does.

In this subsection, goal revision means a change in the acceptable region within a fixed modeling frame. The disturbance space $D$ , the response space $R$ , the possible outcome space $Z$ , the essential-variable space $E$ , the table $T$ , and the outcome-to-essential-variable map $φ$ remain fixed. Thus the same outcome-value keeps the same essential-variable interpretation. What changes is the acceptable region $η_{t_{1}} \subseteq E to η_{t_{2}} \subseteq E$ and therefore the acceptable outcome-set changes from $O_{acc, t_{1}}$ to $O_{acc, t_{2}}$ inside the same essential-variable space $E$ , not the meaning or dimensionality of the essential variables themselves.

If the goal revision changes which variables count as essential, or changes the level at which outcomes are mapped to essential-variable values, then $E$ or $φ$ must also be revised; that would be a different modeling case.

This is goal revision within a fixed repertoire, not structural adaptation. That distinction is important because stronger Ashby-style adaptation involves change in the system's structure, organization, or available repertoire, not merely a different rule selected from the same fixed table[1].

In a higher-order system, revising the acceptable set may itself be part of a meta-regulatory process[57]. Here, goal revision is treated as an external change in the criterion of success, not as regulation by the fixed first-order regulator. It could be modeled as higher-order regulation in a larger adaptive system, but that is outside the fixed-table case considered here.

A change in the acceptable set is not yet a change in actual behavior. It is a change in the criterion by which behavior is judged. A behavioral change occurs only if the regulator changes its response rule from $ρ_{t_{1}}$ to $ρ_{t_{2}}$ . Such a change is required only when the old rule no longer maps the disturbances under consideration into the revised acceptable outcome-set.

Thus the transition from $η_{t_{1}}$ to $η_{t_{2}}$ first changes the criterion of success. This induces a change from $O_{acc, t_{1}}$ to $O_{acc, t_{2}}$ . The old response rule $ρ_{t_{1}}$ must then be tested against the revised acceptable outcome-set. If $y_{t_{1}} [D] \subseteq O_{acc, t_{2}}$ , then the old behavior remains successful under the new criterion. If not, regulation requires selecting a revised response rule $ρ_{t_{2}}$ such that $y_{t_{2}} [D] \subseteq O_{acc, t_{2}}$ . Goal revision is not itself regulation. Continued regulation after goal revision requires that some response rule — possibly the old one, possibly a revised one — maps the disturbances under consideration into the revised acceptable outcome-set.

We are therefore tracking acceptability at the level of outcome-values in $Z$ , via the pullback along φ. Acceptability-status is time-indexed, while outcome-identity in $Z$ is not. So the change is not that outcome-values disappear from the table. The change is that some fixed outcome-values in $Z$ may cease to be acceptable, while others may become acceptable. That is why it is correct to time-index O_acc,t.

Before defining deletion and addition at the level of outcome-values, one qualification is needed. If acceptability is defined by pulling back the acceptable essential-variable region along φ, then acceptability is constant on the fibers of φ.

F_{e} := φ^{- 1} [{e}] = {z \in Z : φ (z) = e}

The set $F_{e}$ is the fiber of outcome-values that all correspond to the same essential-variable value $e$ . If $O_{acc, t} := φ^{- 1} [η_{t}]$ , then all members of the same fiber have the same acceptability-status at time t.

z, z^{'} \in F_{e} \Rightarrow z \in O_{acc, t} \Leftrightarrow z^{'} \in O_{acc, t}

When acceptability is defined by pullback from $η_{t}$ , acceptability cannot vary inside a fiber of φ. If two distinct outcome-values map to the same essential-variable value, they share the same acceptability-status at time t. Therefore, if the modeler wants two outcome-values in the same fiber to have different acceptability-statuses, then the map $φ$ has collapsed a distinction that is relevant for regulation.

This is not a limitation of the set-theoretic construction; it is a consequence of the chosen level of description. If two outcome-values must be judged differently for purposes of regulation, then they cannot be treated as equivalent under the outcome-to-essential-variable map. In that case, $φ$ is too coarse for the regulatory problem being modeled. The outcome-description must be refined, or the mapping must be replaced by a relation, a more detailed essential-variable space, or a probabilistic mapping.

Therefore, in the many-to-one case, deletion and addition of acceptable outcome-values is not truly individual. It happens fiber-wise. Because acceptability is defined by pulling back the acceptable essential-variable region $η_{t}$ along $φ$ , one cannot remove one member of a fiber from the acceptable set while leaving another member of the same fiber acceptable.

Revision of acceptability: deletion, addition, and substitution within the acceptable outcome-set

With this interpretation, the notions of deletion, addition, and substitution are legitimate, provided they are understood as operations on the acceptable subset O_acc,t, not on the table T itself. So no outcome-value is deleted from the table T. Rather, some fixed outcome-values may lose or gain acceptability.

An outcome-value z is deleted from the acceptable set between t₁ and t₂ iff

z \in O_{acc, t_{1}} and z \notin O_{acc, t_{2}} .

This does not mean that z disappears from the table T. It means only that z, though still a possible outcome-value in T, is no longer acceptable under the revised goal.

These definitions concern changes in acceptability-status only. They do not imply that the regulator actually produces, stops producing, or replaces those outcome-values. Behavioral change is tracked separately by comparing $y_{t_{1}} [D]$ and $y_{t_{2}} [D]$ .

An outcome-value z is added to the acceptable set between t₁ and t₂ iff

z \notin O_{acc, t_{1}} and z \in O_{acc, t_{2}} .

In the minimal set-theoretic sense, a weak substitution occurs when one acceptable outcome loses acceptability and another gains acceptability between t₁ and t₂. That is, there exist b, c ∈ $Z$ such that

b \in O_{acc, t_{1}} ∖ O_{acc, t_{2}}, c \in O_{acc, t_{2}} ∖ O_{acc, t_{1}} .

Then one may say that b is removed from the acceptable set and c is admitted into it. This expresses substitution as coexistence of loss and gain; a stronger one-for-one replacement notion would require an additional correspondence between lost and gained elements.

It is useful to decompose the transition from t₁ to t₂ into three parts.

The persistently acceptable outcomes are

P_{12} := O_{acc, t_{1}} \cap O_{acc, t_{2}} = φ^{- 1} [η_{t_{1}} \cap η_{t_{2}}] .

Equivalently, changes in acceptable outcome-values are the pullbacks of changes in acceptable essential-variable values. If $O_{acc, t} := φ^{- 1} [η_{t}]$ , then the outcome-values that lose acceptability between t₁ and t₂ are:

L_{12} := O_{acc, t_{1}} ∖ O_{acc, t_{2}} = φ^{- 1} [η_{t_{1}} ∖ η_{t_{2}}] .

The outcome-values that gain acceptability between t₁ and t₂ are:

G_{12} := O_{acc, t_{2}} ∖ O_{acc, t_{1}} = φ^{- 1} [η_{t_{2}} ∖ η_{t_{1}}] .

This makes the fiber-wise character explicit. If several distinct outcome-values $z$ map to the same essential-variable value $e$ , then they enter or leave the acceptable outcome-set together. The reason is that acceptability is assigned first to essential-variable values and only then transferred back to outcome-values through $φ$ .

Thus, in the reduced or bijective case, each relevant fiber contains exactly one outcome-value, so deletion and addition can be read directly at the level of individual outcome-values. In the many-to-one case, however, deletion and addition should be read as operations on whole fibers of $φ$ .

Then

O_{acc, t_{2}} = (O_{acc, t_{1}} ∖ L_{12}) \cup G_{12} .

and the disjoint unions of the persistently acceptable outcomes and the outcomes that lose and gain acceptability are given by: $O_{acc, t_{1}} = P_{12} \dot{\cup} L_{12}$ $O_{acc, t_{2}} = P_{12} \dot{\cup} G_{12}$

Thus deletion, addition, and substitution are operations on acceptability-status within the fixed outcome-space $Z$ , not on the existence of values in T itself.

This models the attempt to maintain regulation under an externally revised criterion of success within a fixed repertoire. It is not structural adaptation in the stronger sense, because the regulator does not alter its own structure or acquire a new repertoire. Stronger adaptation enters only when the fixed repertoire is no longer sufficient and the system must reorganize itself.

Strict substitution

A strict substitution is stronger than the mere coexistence of loss and gain. Weak substitution says only that some outcome-values lose acceptability and some other outcome-values gain acceptability. Strict substitution says, in addition, that the model supplies a specified replacement correspondence between the lost and gained outcome-values.

Using the earlier definitions:

L_{12} := O_{acc, t_{1}} ∖ O_{acc, t_{2}}

G_{12} := O_{acc, t_{2}} ∖ O_{acc, t_{1}}

A strict substitution structure from t₁ to t₂ is an ordered triple

(L_{12}, G_{12}, σ_{12})

such that:

L_{12} \neq \emptyset and G_{12} \neq \emptyset

and the model supplies a specified bijection

λ_{12} : L_{12} \to G_{12}

where λ₁₂ is not merely a bijection whose existence follows from equal cardinalities. It is part of the model. It specifies which lost acceptable outcome-value is treated as replaced by which newly acceptable outcome-value.

Thus,

λ_{12} (b) = c

means that the previously acceptable outcome-value b is replaced, under the revised criterion of success, by the newly acceptable outcome-value c.

Strict substitution is still a relation between acceptability-statuses. It says that the revised criterion treats newly acceptable outcome-value c as the specified replacement for previously acceptable outcome-value b. It does not, by itself, imply that the regulator has actually produced c as a behavioral replacement for b. That would require an additional closure event or a change in the response rule.

The existence of a bijection requires

| L_{12} | = | G_{12} |

but this equality is only a necessary cardinality condition. It does not determine which lost outcome-value corresponds to which gained outcome-value. The transition of acceptable sets determines only the lost set and the gained set. It does not, by itself, determine the replacement pairing.

Therefore, replacement is not objectively present in the set transition alone. Weak substitution is present in the set transition whenever loss and gain coexist. Strict substitution requires additional correspondence structure.

In the special one-for-one case, where exactly one outcome-value loses acceptability and exactly one outcome-value gains acceptability, strict substitution reduces to:

L_{12} = {b} and G_{12} = {c}

In that case there is only one possible bijection, so one may say that b is strictly substituted by c.

This defines strict substitution at the outcome-value level. In the many-to-one case, one may instead define strict substitution at the essential-variable level by pairing lost and gained elements of $η_{t_{1}} ∖ η_{t_{2}}$ and $η_{t_{2}} ∖ η_{t_{1}}$ . The outcome-level and essential-variable-level notions coincide in the reduced or bijective case. Strict substitution at the outcome-value level may fail in the many-to-one case even when strict substitution exists at the essential-variable level, because fibers $φ$ may have unequal cardinalities.

Behavioral rework

The preceding definitions describe revision of acceptability-status. They do not yet describe behavioral rework. Behavioral rework concerns a change in the outcome-values actually selected by the regulator's response rule. Thus, an outcome-value $z$ is behaviorally removed between t₁ and t₂ iff:

z \in y_{t_{1}} [D] and z \notin y_{t_{2}} [D] .

It is behaviorally added iff:

z \notin y_{t_{1}} [D] and z \in y_{t_{2}} [D] .

Therefore, goal revision changes the criterion of success; behavioral rework changes the regulator's selected outcomes. The two are related but not identical. A goal revision may require no behavioral rework if the old response rule remains successful under the revised acceptable outcome-set.

Information-Theoretic Formulation

The set-based formulation specifies the regulatory problem in terms of value spaces, the Table of Outcomes, the outcome-to-essential-variable map, and the acceptable region. The information-theoretic formulation keeps that same structure and adds probability distributions over it. It does not introduce a different regulatory model; it measures uncertainty, variety, buffering, and knowledge over the same disturbance-values, response-values, outcome-values, and essential-variable values.

Random variables over the set-based regulatory geometry

At time t, let $D_{t}$ , $R_{t}$ , $Z_{t}$ , and $E_{t}$ denote, respectively, the disturbance random variable, regulatory-response random variable, outcome-value random variable, and essential-state random variable. These random variables are functions into the value spaces introduced above:

$D_{t} : Ω_{t} \to D, R_{t} : Ω_{t} \to R, Z_{t} : Ω_{t} \to Z, E_{t} : Ω_{t} \to E .$

Thus their realized values satisfy $d \in D$ , $r \in R$ , $z \in Z$ , and $e \in E$ .

The disturbance distribution P_t(D_t) describes how probability mass is distributed over the disturbance-values under consideration. The regulator's response policy is represented by P_t(R_t | D_t). In the deterministic case, this policy reduces to a response rule:

ρ_{t} : D \to R,

meaning that P_t(R_t = r | D_t = d) = 1 exactly when r = ρ_t(d).

Given the Table of Outcomes T : 𝒟 × 𝓡 → 𝒵, the disturbance and response variables induce the outcome-value variable:

Z_{t} = T (D_{t}, R_{t}) .

The corresponding essential-state variable is obtained by applying the outcome-to-essential-variable map:

E_{t} = φ (Z_{t}) = φ (T (D_{t}, R_{t})) .

Under the fixed-table assumption used here, the system transition is deterministic: once d and r are fixed, z = T(d,r) and e = φ(z) are fixed. A stochastic plant would require replacing the indicator terms below with conditional probability kernels.

Equivalently, the joint distribution is concentrated on tuples satisfying the structural constraints imposed by T and φ:

$P_{t} (d, r, z, e) = P_{t} (d) P_{t} (r | d) 1 [z = T (d, r)] 1 [e = φ (z)] .$

Thus the information-theoretic formulation measures uncertainty over the same regulatory geometry already defined in the set-based formulation. The Table of Outcomes determines which outcome-value is produced by a disturbance-response pair, and φ determines which essential-variable value is associated with that outcome-value.

Entropy, variety, and the outcome-to-essential-variable map

Shannon entropy, denoted by H, measures uncertainty over distinguishable values of a random variable. For a finite random variable X with distribution P(X), entropy is:

H (X) = - \sum_{x \in supp (X)}^{} P (x) \log_{2} P (x) .

When all values in the finite support of X are equiprobable, entropy reduces to the logarithm of count-variety:

H (X) = \log_{2} | supp (X) | .

More generally, entropy is the probabilistic analogue of variety. It measures how much uncertainty remains about which distinguishable value of a variable will be realized.

Because E_t = φ(Z_t), the essential-state variable is a function of the outcome-value variable. Therefore:

H (E_{t}) \leq H (Z_{t}) .

More precisely:

H (Z_{t}) = H (E_{t}) + H (Z_{t} | E_{t}) .

In the reduced or bijective case, H(Z_t|E_t) = 0, so the outcome-value variable and the essential-state variable are informationally equivalent on the relevant support:

H (Z_{t}) = H (E_{t}) .

In the many-to-one case, φ collapses several distinct outcome-values into the same essential-variable value. Then outcome-level uncertainty may be greater than essential-variable uncertainty. Equality holds only when φ is one-to-one on the relevant outcome-values. This distinction matters because regulation is judged at the level of the essential variables, even though the Table of Outcomes produces outcome-values.

Probabilistic success and support-level success

The acceptable region at time t is the set:

η_{t} \subseteq E .

The corresponding acceptable outcome-set is the pullback of that acceptable essential-variable region along φ:

O_{acc, t} := φ^{- 1} [η_{t}] = {z \in Z : φ (z) \in η_{t}} .

Strict probabilistic success at time t means that the essential-state variable lies inside the acceptable region with probability one:

\Pr (E_{t} \in η_{t}) = 1 .

Equivalently, at the outcome-value level:

\Pr (Z_{t} \in O_{acc, t}) = 1 .

In discrete support notation, this is:

supp (E_{t}) \subseteq η_{t}

or equivalently:

supp (Z_{t}) \subseteq O_{acc, t} .

This is the distribution-level probabilistic version of the set-based success condition. It checks the disturbance-values that have positive probability under the current disturbance distribution. If supp(D_t) = 𝒟, then in the deterministic rule-level case it reduces to the universal set-based condition that the rule-induced actual outcome-set lies inside the acceptable outcome-set. If supp(D_t) ⊂ 𝒟, then the probability-one condition is weaker: it guarantees success only over disturbance-values that have positive probability at time t.

For universal rule-level success over the whole modeled disturbance set, the policy must be successful for every disturbance-value under consideration. Here P_t(R_t|D_t=d) is treated as the regulator's policy kernel, defined for every modeled disturbance-value d ∈ 𝒟, not merely for disturbance-values with positive probability under the current disturbance distribution.

Define the acceptable concrete response-set for disturbance d as:

A_{t} (d) := {r \in R : φ (T (d, r)) \in η_{t}} .

Then universal rule-level success requires:

\forall d \in D, supp (P_{t} (R_{t} | D_{t} = d)) \subseteq A_{t} (d) .

In the deterministic case, this condition reduces to:

\forall d \in D, ρ_{t} (d) \in A_{t} (d) .

This distinction matters because probability-one success is a statement about the support of the current distribution, while universal set-based success is a statement about every disturbance-value included in the modeled regulatory problem.

Allowed residual variety

If the acceptable essential-variable region is finite, its maximum allowed essential-variable entropy is:

h_{η, t} := \log_{2} | η_{t} | .

Strict probabilistic success implies the necessary entropy condition:

H (E_{t}) \leq h_{η, t} .

This entropy condition is necessary, not sufficient. A distribution can have low entropy while still placing probability mass outside the acceptable region. Successful regulation requires confinement within η_t, not merely low entropy.

Similarly, if the acceptable outcome-set is finite, its maximum allowed outcome-level entropy is:

h_{O, t} := \log_{2} | O_{acc, t} | .

Strict probabilistic success at the outcome-value level implies:

H (Z_{t}) \leq h_{O, t} .

In the reduced representation, where 𝒵 = 𝓔 and φ = id_𝓔, the acceptable outcome-set is just the acceptable essential-variable region, so h_O,t = h_η,t. In the many-to-one case, however, the outcome-level entropy allowance h_O,t may be larger than the essential-variable entropy allowance h_η,t, because the pullback may include whole fibers of φ back into acceptability.

Response-equivalence and regulatory ignorance

Aulin-Ahmavaara and Heylighen characterize the ignorance term H(R|D) at the level of disturbance, regulator action, and quality of regulation. They describe it as uncertainty about how to react correctly to a disturbance and how to use the available regulatory acts optimally — using "correctly" and "optimally" loosely as near-synonyms rather than as a deliberate two-level distinction. However, their prose does not fully fix the granularity of the response variable R. It leaves open whether the response denotes: (i) an equivalence class of concrete responses that achieve the same acceptable outcome, (ii) the exact concrete response emitted by the regulator, or (iii) the optimal response among several acceptable responses[29][31].

The term H(R_t|D_t) measures uncertainty over which concrete response-value the regulator will use after the disturbance is known. That is useful, but it can overcount ignorance if several concrete responses are equivalent for the adopted success criterion. Entropy only measures uncertainty over the variable supplied to it; it does not know which distinctions matter for regulation.

To avoid counting irrelevant implementation variation as ignorance, we introduce response-equivalence classes. “Response-equivalence” means that two concrete responses belong to the same response class if the model treats them as interchangeable for the regulatory purpose being analyzed. At the coarsest success-preserving granularity, two concrete responses are placed in different classes only if choosing between them can matter to whether the resulting outcome is acceptable under the adopted success criterion.

For a fixed time t, let g_t : 𝓡 → 𝓧_t map each concrete response-value to a response-equivalence class. Each element of 𝓧_t is therefore a subset of 𝓡. The partition 𝓧_t should be chosen at the coarsest granularity that still preserves distinctions relevant to the adopted valuation and success criterion. The response-class random variable is:

X_{t} := g_{t} (R_{t}) .

One natural acceptability-based response-equivalence requirement is:

$g_{t} (r_{1}) = g_{t} (r_{2}) \Rightarrow \forall d \in D [φ (T (d, r_{1})) \in η_{t} \Leftrightarrow φ (T (d, r_{2})) \in η_{t}] .$

That is, two concrete responses may be placed in the same class only if replacing one with the other never changes success or failure under the adopted regulatory criterion. This weaker version is enough when regulation only asks: Did the outcome fall inside the acceptable region?

If the model needs to preserve exact essential-variable values rather than merely acceptability-status, a stronger valuation-based response-equivalence requirement may be used:

$g_{t} (r_{1}) = g_{t} (r_{2}) \Rightarrow \forall d \in D [φ (T (d, r_{1})) = φ (T (d, r_{2}))] .$

The weaker success-equivalence relation is appropriate when only membership in the acceptable region matters. The stronger valuation-equivalence relation is appropriate when different acceptable essential-variable values must still be distinguished. If the modeler wants the coarsest possible partition, the corresponding implication can be strengthened to a biconditional. “Response-equivalence” is important because it determines what uncertainty counts as regulatory ignorance.

Using the acceptable concrete response-set 𝒜_t(d) defined above, the corresponding acceptable response-class set is:

X_{acc, t} (d) := {x \in X_{t} : x \subseteq A_{t} (d)} .

In words, a response-class is acceptable for disturbance d when every concrete response in that class is acceptable for d. If a proposed class contains both acceptable and unacceptable concrete responses, then the class is too coarse for the adopted success criterion and must be refined.

Regulator's learned law of action

The regulator's accumulated structure M_t is its learned law of action: its prior knowledge about disturbances, available responses, outcome consequences, and success-relevant distinctions. In the deterministic case, this learned structure may be represented as a response rule:

M_{t} : D \to R .

In the general case of learning and uncertainty, M_t induces a response policy:

M_{t} \Rightarrow P_{M_{t}} (R_{t} | D_{t}) .

This policy describes how probability mass is allocated across possible response-values or response-classes for each disturbance-value, given the regulator's current knowledge state. If the Table of Outcomes T is the fixed space of possibilities, then M_t is the learned structure that induces a probability distribution over possible paths through that table.

Across time, M_t need not remain fixed. Changes in M_t alter which disturbance-response pairs become more or less probable, and therefore how the system's realized trajectories are distributed over the Table of Outcomes. Successful learning shifts probability mass away from ineffective responses and toward responses that better compensate the same disturbances.

All probabilities, entropies, and mutual informations used to describe the regulator's knowledge state can therefore be read epistemically, relative to M_t. When that dependence matters, we write P_{M_t} and H_{M_t}. When it is clear from context, the subscript is suppressed.

When the regulator's response variation is both disturbance-specific and correct for the Table of Outcomes, M_t reduces residual outcome or essential-variable variety. However, correctness is still judged by the set-based success condition:

\Pr (Z_{t} \in O_{acc, t}) = 1

or, equivalently:

\Pr (E_{t} \in η_{t}) = 1 .

Knowledge To Be Discovered

Let Y_t denote the disturbance information available to the regulator. In the simplest fully observed case, Y_t = D_t. In a partially observed case, Y_t may be only a signal, observation, or classification of the disturbance.

For a particular observation-value y, define the disturbance-values still possible under that observation as:

D_{t} (y) := {d \in D : P_{M_{t}} (D_{t} = d | Y_{t} = y) > 0} .

Then the acceptable response-class set under observation y is:

X_{acc, t} (y) := ⋂_{d \in D_{t} (y)}^{} X_{acc, t} (d) .

Thus, under partial observation, a response-class is safely acceptable only if it works for every disturbance-value still possible under the regulator's observation. If this intersection is empty, then no response-class is guaranteed to succeed under that observation without additional information, additional buffering, or a richer response repertoire.

If the regulatory problem is modeled as requiring a unique valuation-based response-equivalence class for each disturbance-value, let q_t : 𝒟 → 𝓧_t denote the target-class map. The required response-class random variable is then:

X_{t}^{*} := q_{t} (D_{t}) .

Under this unique-target assumption, the regulator's remaining epistemic ignorance after the available disturbance information is known is:

H_{M_{t}} (X_{t}^{*} | Y_{t}) .

When the dependence on M_t is clear from context, this may be written more simply as H(X|Y).

In this article, H(X|Y) is called Knowledge To Be Discovered: the remaining uncertainty, after the available disturbance information is known, about which required target response-equivalence class must be fixed for successful regulation.

Knowledge To Be Discovered is defined by the conditional entropy of the required target class: H(X_t^*|Y_t). It is not generally defined by H(X_t|Y_t), because X_t may describe the regulator's actual policy variation rather than the response-class that success requires, unless you explicitly assume:

X_{t} = X_{t}^{*}

That assumption is strong. It means the regulator’s actual response-class variable is already aligned with the required target-class variable. Without that alignment, H(X_t|Y_t) can measure randomness, indecision, exploration, implementation variation, or even consistently wrong behavior — not necessarily knowledge still to be discovered. However, correctness is a separate matter. A regulator may be perfectly selective and still wrong. Therefore, Knowledge To Be Discovered must be paired with a success/misalignment condition if the model is to distinguish uncertain regulation from confidently wrong regulation.

In the more general set-valued case, where several response-classes are acceptable for the same disturbance or observation, Knowledge To Be Discovered is not a single conditional entropy unless the model adds a selection criterion that turns the acceptable set into a target-class variable.

The H(X|Y) should be used as Knowledge To Be Discovered only after the model specifies a selection criterion that makes one class the target. Otherwise, uncertainty among several equally acceptable response-classes is not necessarily regulatory ignorance. Successful regulation requires only that the class eventually fixed by the regulator lie inside the acceptable response-class set, not identification of one uniquely correct class:

X_{t} \in X_{acc, t} (Y_{t}) .

This is the key distinction: uncertainty over concrete responses is not automatically ignorance. It becomes regulatory ignorance only when the unresolved distinction matters for achieving an acceptable outcome under the adopted success criterion.

If X_t is a quotient of the concrete response variable R_t, then X_t is determined by R_t. Therefore:

H_{M_{t}} (X_{t} | Y_{t}) \leq H_{M_{t}} (R_{t} | Y_{t}) .

More explicitly, since X_t = g_t(R_t):

H_{M_{t}} (R_{t} | Y_{t}) = H_{M_{t}} (X_{t} | Y_{t}) + H_{M_{t}} (R_{t} | X_{t}, Y_{t}) .

The second term, H(R_t|X_t,Y_t), is residual uncertainty over which concrete response inside the already-fixed response-equivalence class will be emitted. That residual uncertainty is not necessarily regulatory ignorance. It may simply be implementation variation.

For example, suppose the disturbance is “pay $10,” and both “use one $10 bill” and “use ten $1 bills” are equally acceptable from the valuation layer's point of view. These are different concrete response-values, but they belong to the same response-equivalence class if the adopted success criterion cares only that $10 is paid. In that model, uncertainty between those concrete responses should not increase Knowledge To Be Discovered.

If the environment later cares about speed, accounting policy, fraud risk, or change preservation, then “one $10 bill” and “ten $1 bills” may no longer be equivalent. They should then be separated into different response-equivalence classes. In that revised model, uncertainty over which bill combination to use is genuine lack of requisite knowledge.

Thus, X_t must be defined at the right granularity. If X_t is too fine, the model counts irrelevant implementation variation as ignorance. If X_t is too coarse, the model hides distinctions that matter for success. Knowledge To Be Discovered is meaningful only when the response-equivalence classes preserve exactly the distinctions required by the adopted regulatory criterion.

Therefore, response-equivalence is the bridge between the entropy formula and Ashby's regulatory success condition. Without it, H(X|Y) is merely uncertainty over a chosen response variable. With it, H(X|Y) is uncertainty over the response variable at the regulatory granularity being analyzed: the uncertainty that must still be resolved for successful regulation.

Knowledge To Be Discovered and effective regulatory knowledge

The preceding definition of Knowledge To Be Discovered is not separate from the mutual-information terms used in the Ashby-style formulation below. It is the complementary uncertainty term in the same entropy decomposition.

Under the unique-target assumption, X_t^* is the response-equivalence class that must be fixed for successful regulation. The total uncertainty over required response-classes is:

H (X_{t}^{*}) = I (X_{t}^{*}; Y_{t}) + H (X_{t}^{*} | Y_{t}) .

The mutual-information term I(X_t^*;Y_t) measures how much the available observation reduces uncertainty about the required response-class. The conditional-entropy term H(X_t^*|Y_t) is Knowledge To Be Discovered: the remaining uncertainty about which response-class must be fixed.

Thus Knowledge To Be Discovered and effective regulatory knowledge are two sides of the same decomposition:

$Knowledge To Be Discovered = H (X_{t}^{*}) - I (X_{t}^{*}; Y_{t}) .$

In the fully observed case, where Y_t = D_t, this becomes:

H (X_{t}^{*} | D_{t}) = H (X_{t}^{*}) - I (X_{t}^{*}; D_{t}) .

This is the response-class version of Aulin-Ahmavaara's ignorance term. At the correct regulatory granularity, the effective knowledge available to the regulator is the part of required response-class variety already determined by the disturbance information. The Knowledge To Be Discovered is the part not yet determined.

Therefore, the later mutual-information term I(S_t;D_t) should be read as an effective regulatory-knowledge term only when S_t is defined at the same success-relevant granularity as the required response-class variable. In the unique-target case, this means setting S_t = X_t^*. If S_t denotes concrete responses or some other granularity, the mutual-information term measures disturbance-response coupling, but not necessarily Knowledge To Be Discovered.

Ashby-style residual-variety bounds

The preceding success conditions are exact confinement conditions. A variety inequality is not the definition of success; it is a necessary numerical consequence under additional assumptions.

In the idealized finite-table case, where disturbances and responses are treated as distinguishable possibilities, the Ashby-style count-variety lower bound can be written as:

V (y_{t} [D]) \geq ⌈ \frac{V (D)}{V (R)} ⌉ .

In logarithmic form, and ignoring the ceiling for the idealized entropy analogue, this becomes:

\log_{2} V (y_{t} [D]) \geq \log_{2} V (D) - \log_{2} V (R) .

This expression should be read as an idealized lower-bound form, not as a general theorem about every possible Table of Outcomes. It assumes that disturbance variety is not already collapsed by the table structure except for any explicitly modeled buffering or passive absorption. If the table itself collapses several disturbance-values into the same outcome-value, then the lower bound must be modified to reflect that additional collapse.

The preceding subsection defined Knowledge To Be Discovered at the level of the required response-equivalence class. The Ashby-style residual-variety bound can now be written using a general response variable S_t, where S_t is the response variable at the regulatory granularity being analyzed. If concrete response-values are relevant, then S_t = R_t. If response-equivalence classes are the relevant units, two cases must be distinguished. If S_t denotes the actual response-class emitted by the regulator, then S_t = X_t. If S_t denotes the required target response-class, then S_t = X_t^*. Thus S_t is not a new kind of response; it is a placeholder for the response-level at which regulatory knowledge and residual variety are being measured.

Under the same idealizing assumptions as the finite-table quotient argument — no unmodeled table collapse except buffering K, a response variable S_t defined at the same regulatory granularity as the outcome variable being bounded, and correct disturbance-specific compensation — the following Shannon-style residual-variety analogue may be written:

H (Z_{t}) \geq {[H (D_{t}) + H (S_{t} | D_{t}) - H (S_{t}) - K]}_{+} .

Here [a]₊ := max(a,0), since residual entropy cannot be negative. The term K denotes buffering capacity: disturbance variety absorbed passively before active regulation is required. This equation should be read as an information-theoretic analogue of Ashby's finite-table lower-bound argument under the stated idealizing assumptions.

Since:

H (S_{t}) - H (S_{t} | D_{t}) = I (S_{t}; D_{t}),

the same bound can be written compactly as:

H (Z_{t}) \geq {[H (D_{t}) - I (S_{t}; D_{t}) - K]}_{+} .

The mutual information I(S_t;D_t) measures how much the regulator's response variable, at the chosen regulatory granularity, is coupled to disturbance variation.

H_{eff} (S_{t}) := I (S_{t}; D_{t}) = H (S_{t}) - H (S_{t} | D_{t}) .

This is a measure of disturbance-specific response selection at the regulatory granularity being analyzed. By itself, however, it is not a guarantee of correctness. A response can be strongly coupled to a disturbance and still be the wrong response for the Table of Outcomes. Under the additional assumption that the coupling maps disturbances to appropriate compensating responses, it can be interpreted as requisite regulatory knowledge.

The outcome-level residual-variety bound can therefore be written as:

H (Z_{t}) \geq {[H (D_{t}) - H_{eff} (S_{t}) - K]}_{+} .

Combining this lower bound with the allowed outcome-level residual variety gives the following necessary feasibility condition for strict success:

H_{eff} (S_{t}) + K \geq H (D_{t}) - h_{O, t} .

In the reduced or bijective case, where the acceptable outcome-set and the acceptable essential-variable region have the same relevant variety, this becomes:

H_{eff} (S_{t}) + K \geq H (D_{t}) - h_{η, t} .

Expanded, this is:

H (S_{t}) \geq H (D_{t}) + H (S_{t} | D_{t}) - K - h_{η, t} .

If this necessary condition fails under the stated assumptions, strict success is impossible. If it holds, success is still not guaranteed; the response mapping must still be appropriate for the actual Table of Outcomes. The decisive success condition remains the confinement condition:

\Pr (E_{t} \in η_{t}) = 1 .

In the many-to-one case, the outcome-level and essential-variable-level statements must be kept distinct. A lower bound on H(Z_t) does not automatically imply the same lower bound on H(E_t), because φ may collapse outcome distinctions that are irrelevant at the essential-variable level. The safer formulation is therefore to write the bound first for Z_t and then relate Z_t to E_t through E_t = φ(Z_t).

Point regulation

In the special case of point regulation, the acceptable region contains only one essential-variable state:

| η_{t} | = 1 and therefore h_{η, t} = 0 .

Under the reduced or bijective representation, the necessary feasibility condition becomes:

H_{eff} (S_{t}) + K \geq H (D_{t}) .

Equivalently:

H (S_{t}) \geq H (D_{t}) + H (S_{t} | D_{t}) - K .

In the ideal best-opportunity case, where buffering is ignored, the response policy is deterministic at the relevant regulatory granularity, and the response mapping is correct, this reduces to:

H (S_{t}) \geq H (D_{t}) .

This should be read as an optimal-control limit, not as a blanket claim that every control problem is solved whenever response entropy is at least as large as disturbance entropy. The response mapping must also select the right response-values or response-classes for the actual Table of Outcomes, so that the induced outcome-values fall inside the acceptable outcome-set.

The deterministic-policy assumption means that the regulator's response variable at the chosen regulatory granularity is fully determined by the disturbance: H(S_t|D_t) = 0. This represents complete requisite knowledge only under the additional assumption that the learned response mapping sends each disturbance to an appropriate regulatory act. A regulator can deterministically choose the wrong response; therefore, zero conditional entropy alone does not prove correct regulation.

Successful essential-variable outcomes do not depend solely on the amount of response variety available to a regulator. The system must also be able to select the appropriate response for the given disturbance. Effective compensation of disturbances requires that the system possess a mapping from disturbances to appropriate responses within its repertoire. The absence or incompleteness of such knowledge can be represented by the conditional entropy H(S_t|D_t) only when S_t denotes the required response-class variable, or when the actual response variable is assumed to be aligned with the correct target mapping. Otherwise, zero conditional entropy means only that the response is determined by the disturbance; it does not by itself mean that the selected response is correct.

In other words, H(S_t | D_t) measures how much uncertainty remains about the regulator's response at the chosen regulatory granularity after the disturbance is known. Under the regulatory correctness assumption, this uncertainty corresponds to lack of requisite knowledge. Merely increasing response variety is therefore not sufficient. It must be complemented by a corresponding increase in selectivity: a reduction in H(S_t | D_t), i.e. an increase in knowledge. This requirement may be called the law of requisite knowledge[29].

The larger H(S_t | D_t) is, the less selectively the regulator's actions are determined by the disturbance. Under the assumption that each disturbance requires a limited set of appropriate responses at the chosen regulatory granularity, this increases the risk of selecting an ineffective response. Therefore, the term H(S_t | D_t) has a plus sign in the inequality: more uncertainty about how to respond increases the lower bound on residual outcome or essential-variable variety[54].

The information-theoretic formulation therefore does not replace the set-based success condition. It measures the uncertainty, variety, buffering, and knowledge involved in satisfying that condition. The set-based section gives the geometry of the regulatory problem; the information-theoretic section puts probability mass over that same geometry and measures the remaining uncertainty in bits.

Knowledge Discovery Process

The process of selection may be either more or less spread out in time. In particular, it may take place in discrete stages. What is fundamental quantitatively is that the overall selection achieved cannot be more than the sum (if measured logarithmically) of the separate selections. (Selection is measured by the fall in variety.) 13/17[2]

Ashby's selection in design and regulation share the same abstract selection schema: both reduce a space of possible alternatives by applying constraints, tests, rules, observations, or feedback. In regulation, however, the regulator does not select an outcome-value directly. It selects a response-value in the presence of a disturbance-value; the Table of Outcomes then determines the resulting outcome-value, and the outcome-to-essential-variable map determines whether that outcome is acceptable.

Importantly, so far we assumed that the regulator selects a response-value to a given disturbance-value in a single step. However, in many real-world regulatory problems, the regulator does not select a response-value in a single step. Instead, the regulator may select a response-value in stages, where each stage of selection may depend on the disturbance-value and on the response-values selected in previous stages. For example, a regulator may first select a coarse response-value, and then refine that coarse response-value in subsequent stages of selection. To capture this staged selection we now add time to the notation to indicate that the candidate response-sets are generated by a process of selection that unfolds over time.

Throughout this subsection, the index $t$ denotes the staged selection trace index at which the disturbance, knowledge state, acceptable region, and committed response are evaluated. It does not index the internal stages of the staged selection trace. The internal stages of a staged selection trace are indexed by $i = 0, \dots, k$ . Thus a staged selection trace at time $t$ may contain several internal selection stages, but those stages are represented by the stage index $i$ , not by changing the external selection trace time index.

Each stage of selection may have different length. The emistion of a response-value at the of a selection tarce may alos have different length. However, the time index of the selection trace is not changed by the internal stages of selection or by the emission of a response-value. The time index of the selection trace only changes when the regulator commits to a response-value and emits that response-value to the environment.

Unless explicitly stated otherwise, the acceptable region $η_{t}$ and the knowledge state $M_{t}$ are treated as the regulatory frame for the selection trace indexed by $t$ .

Set-based Formulation of Staged Selection

Using the set-based formulation above, for a disturbance-value $d \in D$ and a response-value $r \in R$ , the outcome-value is $T (d, r) \in Z$ . The corresponding essential-variable value is $φ (T (d, r)) \in E$ . At time $t$ , this response is successful exactly when that essential-variable value lies in the acceptable region $η_{t} \subseteq E$ .

Equivalently, the acceptable outcome-set at time $t$ is the pullback of the acceptable essential-variable region:

O_{acc, t} := φ^{- 1} [η_{t}] = {z \in Z : φ (z) \in η_{t}} .

For a given disturbance-value $d$ , define the acceptable response-set at time $t$ as:

A_{t} (d) := {r \in R : T (d, r) \in O_{acc, t}} .

This is just the pullback of the acceptable outcome-set through the row of the table T corresponding to disturbance d.

Equivalently:

A_{t} (d) = {r \in R : φ (T (d, r)) \in η_{t}} .

The set $A_{t} (d)$ contains exactly those response-values that would produce an acceptable outcome-value for the disturbance-value $d$ under the criterion of success prevailing at time $t$ .

We can now define the set-based staged selection trace as the nested reduction of candidate response-values for a realized disturbance-value. For a particular disturbance-value $d$ , let

\emptyset \neq C_{k} (d) \subseteq \dots \subseteq C_{1} (d) \subseteq C_{0} (d) \subseteq R

be a nested sequence of candidate response-sets. Here, $C_{0} (d)$ is the initial set of response-values available or considered for disturbance $d$ . Each stage applies a constraint, observation, test, rule, model, or feedback signal that removes response-values no longer admissible under the current regulatory problem.

The set-based trace is strongly successful when the remaining candidate response-values are all acceptable:

\emptyset \neq C_{k} (d) \subseteq A_{t} (d) .

In the limiting case, the process fixes a single acceptable response-value:

C_{k} (d) = {r_{t}} with r_{t} \in A_{t} (d) .

Thus, the set-based staged selection trace is the staged reduction of candidate responses until the regulator can commit a response-value that maps the present disturbance into the acceptable outcome-set. The candidate response-set $C_{i} (d)$ represents the remaining support of response-values still admissible after stage $i$ for the realized disturbance-value $d$ . This is a support-level description. It records which response-values remain possible.

Action-unit protocols as partition-refinement updates

The staged candidate trace can be generated by an ordered action-unit protocol. For the episode indexed by $t$ , let

Q_{t} := (q_{t, 1}, \dots, q_{t, k_{t}})

denote the action-unit protocol used inside that episode. Each $q_{t, i}$ is an action unit: a test, observation, constraint, feedback step, model application, partial execution, or other discriminating operation performed at internal stage $i$ . The realized result of that action unit is the signal $U_{t, i} = u_{t, i}$ . Thus the action unit specifies the discriminating operation, while the realized signal selects which candidate responses remain compatible with the realized episode path.

At the set level, an action unit induces a partition of the concrete response space. Let $h_{q_{t, i}}$ be the signal map associated with action unit $q_{t, i}$ :

h_{q_{t, i}} : R \to U_{q_{t, i}} .

For a realized signal-value $u_{t, i}$ , the selected partition block is:

P_{q_{t, i}, u_{t, i}}^{R} := {r \in R : h_{q_{t, i}} (r) = u_{t, i}} .

The induced set-update operator is denoted separately from the protocol. It is:

Γ_{q_{t, i}, u_{t, i}}^{R} : 𝒫 (R) \to 𝒫 (R)

with:

Γ_{q_{t, i}, u_{t, i}}^{R} (C) := C \cap P_{q_{t, i}, u_{t, i}}^{R} .

The operator is contractive: it does not introduce new candidate responses. It only preserves or removes candidates from the current candidate set.

Γ_{q_{t, i}, u_{t, i}}^{R} (C) \subseteq C .

Therefore, the stage transition is:

C_{t, i}^{R} (d) = Γ_{q_{t, i}, u_{t, i}}^{R} (C_{t, i - 1}^{R} (d))

or equivalently:

C_{t, i}^{R} (d) = C_{t, i - 1}^{R} (d) \cap P_{q_{t, i}, u_{t, i}}^{R} .

Consequently, staged selection is progressive partition refinement:

C_{t, 0}^{R} (d) \supseteq C_{t, 1}^{R} (d) \supseteq \dots \supseteq C_{t, k_{t}}^{R} (d) .

Each inclusion represents one additional action-unit selection. The protocol $Q_{t}$ names the ordered sequence of action units. Each $q_{t, i}$ specifies a discriminating operation. Each realized signal $u_{t, i}$ selects the surviving block. The final candidate set is generated by the successive application of the operator $Γ_{q_{t, i}, u_{t, i}}^{R}$ induced by the protocol $Q_{\leq k}$ .

Rule regulation

The rule-level version is obtained by applying the same idea to response rules rather than individual responses. Let $Π := R^{D}$ be the set of possible response rules $ρ : D \to R$ .

For a rule $ρ \in Π$ , define its induced outcome map by $y_{ρ} (d) := T (d, ρ (d))$ and its image over the modeled disturbance set by $y_{ρ} [D] := {T (d, ρ (d)) : d \in D}$

At a particular moment, the regulator may face one realized disturbance-value. But a response rule is judged by what it would produce for every disturbance-value in the modeled disturbance set $D$ .

Define the successful rule-set at time $t$ as:

Π_{acc, t} := {ρ \in Π : y_{ρ} [D] \subseteq O_{acc, t}} .

The rule-level condition is a universal guarantee over the modeled disturbance set. The episode-level condition is a pointwise condition for one realized disturbance $ρ (d) \in A_{t} (d)$

Equivalently:

Π_{acc, t} = {ρ \in Π : φ [y_{ρ} [D]] \subseteq η_{t}} .

This means a rule succeeds only if it produces acceptable outcomes for every modeled disturbance.

A rule-level staged selection trace is then a nested sequence of candidate rule-sets:

Π_{0} \supseteq Π_{1} \supseteq \dots \supseteq Π_{k}

The process succeeds at the rule level when the remaining candidate rules are successful:

\emptyset \neq Π_{k} \subseteq Π_{acc, t} .

In the limiting case, the process fixes a single successful response rule:

Π_{k} = {ρ_{t}} with ρ_{t} \in Π_{acc, t} .

This rule-level formulation is the universal version of the pointwise acceptable-response condition. Equivalently, a rule is successful when, for every modeled disturbance-value $d$ , it selects a response-value in $A_{t} (d)$ .

Therefore, staged response selection is not a process outside regulation. At the set level, it is the nested narrowing of candidate responses or candidate response rules over the disturbance-values under consideration

Episodes and Closures

The set-based staged selection trace, an episode, and a closure describe three different aspects of the same regulatory event. The set-based staged selection trace is the nested reduction of candidate response-values for a realized disturbance-value. An episode is one realized run of that trace. A closure is the realized outcome-value produced when the episode terminates in a committed response-value.

For a selection trace at time $t$ , suppose the realized disturbance-value is $D_{t} = d_{t}$ . An episode at time $t$ is the realized set-based staged selection trace initiated for that disturbance-value. It begins with an initial candidate response-set $C_{t, 0} (d_{t})$ and proceeds through a sequence of internal staged reductions:

\emptyset \neq C_{k} (d) \subseteq \dots \subseteq C_{1} (d) \subseteq C_{0} (d) \subseteq R .

Since t is fixed, we suppress the time index and write $C_{i} (d)$ instead of $C_{t, i} (d_{t})$ for readability.

The selection process terminates when the regulator commits a response-value $r_{t} \in C_{k} (d)$ . This commitment terminates the realized staged selection trace for that episode. The committed response-value then produces the realized outcome-value:

z_{t} := T (d, r_{t}) \in Z .

Thus, a closed episode can be represented by the formal tuple:

ε_{t} (d) := (d, C_{0} (d), \dots, C_{k} (d), r_{t}, z_{t}) .

The closure of the episode is the realized outcome-value produced by the committed response:

cl (ε_{t} (d)) := z_{t} = T (d, r_{t}) .

An acceptable closure is a closure whose realized outcome-value belongs to the acceptable outcome-set prevailing at time $t$ :

cl (ε_{t} (d)) \in O_{acc, t} .

Therefore, there are two different success conditions that should not be confused. A strongly successful staged selection trace terminates with a remaining candidate response-set containing only acceptable responses:

\emptyset \neq C_{k} (d) \subseteq A_{t} (d) .

In that case, any response-value selected from the final candidate set will produce an acceptable closure.

A realized successful episode requires only that the response-value actually committed by the regulator be acceptable:

r_{t} \in A_{t} (d) .

Equivalently:

T (d, r_{t}) \in O_{acc, t} .

Equivalently, the episode has an acceptable closure exactly when the essential-variable value induced by the realized outcome lies inside the acceptable region:

φ (T (d, r_{t})) \in η_{t} .

The strong condition guarantees successful closure before final commitment. The realized condition judges the episode after the committed response has produced its outcome. Therefore, episode closure is defined at the outcome layer. It records that the regulator has committed a response-value and that this commitment has produced a realized outcome-value. Acceptable closure adds the further condition that the realized outcome-value is acceptable under the goal criterion prevailing at time $t$ .

This distinction matters because response commitment and acceptable closure are not identical. A regulator may commit a response-value and still fail to produce an acceptable outcome-value. Conversely, an acceptable closure does not require that only one acceptable response-value was possible. Multiple distinct response-values may map the same disturbance-value into the acceptable outcome-set.

At the set level, staged selection is the process by which a regulator narrows candidate response-values until it can commit a response. An episode is one realized run of that staged selection trace. The episode closes when that committed response, together with the disturbance-value, produces a realized outcome-value. The closure is acceptable when that outcome lies in the acceptable outcome-set $z_{t} \in O_{acc, t}$ . For an acceptable closure:

$d \to C_{0} (d) \supseteq C_{1} (d) \supseteq \dots \supseteq C_{k} (d) \to r_{t} \to z_{t} = T (d, r_{t}) \to z_{t} \in O_{acc, t}$

The set-based staged selection trace does not by itself produce an outcome-value. It narrows the candidate response-set until the regulator can commit a response-value. The Table of Outcomes then maps that committed response-value, together with the disturbance-value, into a realized outcome-value. The episode has an acceptable closure exactly when that realized outcome-value belongs to the acceptable outcome-set prevailing at the time of closure.

Count-Variety Selection

The set-based formulation above defines the episode, the staged selection trace, and the closure. It records which candidate response-values or response rules remain possible after each stage. This is a support-level account. It can be given a logarithmic count-variety interpretation in the finite equiprobable case, but it does not yet define Knowledge To Be Discovered. Knowledge To Be Discovered requires a probability distribution over the required response-equivalence class and is therefore introduced in the information-theoretic formulation.

For finite equiprobable sets, Ashby[13/15 [2]] measures the amount of selection in bits as:

σ = \log_{2} (\frac{V_{b e f o r e}}{V_{a f t e r}}) .

In the present formulation, the “before” and “after” varieties are the cardinalities of explicitly defined candidate sets. For finite candidate response-sets, the count-variety selection achieved at stage $i$ is:

σ_{i}^{set,R} = \log_{2} (\frac{| C_{i - 1} (d) |}{| C_{i} (d) |}) .

This expression assumes that the remaining alternatives are being counted as distinguishable candidate response-values under the adopted modeling resolution i.e. is a concrete-level quantity rather than an class-level quantity. It measures support reduction, not probability-weighted uncertainty reduction. For the present set-based formulation, no probability distribution over $C_{i} (d)$ is required.

The total count-variety selection achieved over a nested staged process is therefore:

σ_{total}^{set,R} = \sum_{i = 1}^{k} σ_{i}^{set,R} = \log_{2} (\frac{| C_{0} (d) |}{| C_{k} (d) |}) .

This additive form is valid when the stages are nested refinements of the candidate set. Each stage must reduce the currently remaining alternatives, not independently recount the original space. If two stages constrain the same distinction in overlapping ways, the second stage's contribution must be counted relative to the alternatives that survived the first stage.

For finite equiprobable rule-sets, the corresponding rule-level count-variety selection at stage $i$ is:

σ_{i}^{rule} = \log_{2} (\frac{| Π_{i - 1} |}{| Π_{i} |}) .

And the total rule-level count-variety selection is:

σ_{total}^{rule} = \sum_{i = 1}^{k} σ_{i}^{rule} = \log_{2} (\frac{| Π_{0} |}{| Π_{k} |}) .

This bridge establishes the count-variety special case. In the finite equiprobable case, and when selection operates purely by eliminating alternatives, logarithmic cardinality reduction coincides with entropy reduction. The information-theoretic formulation generalizes beyond that case by allowing non-uniform probabilities and probability redistribution among surviving candidates. In that formulation, the object being reduced is not merely the candidate set, but the regulator's Knowledge To Be Discovered: the conditional entropy of the required response-equivalence class.

Information-Theoretic Formulation of Staged Selection

What the Information-Theoretic Model Adds

The information-theoretic formulation does not redefine an episode. An episode remains the realized set-based regulatory event defined above. What this subsection adds is a probability model over that episode.

The set-based formulation records the realized regulatory trace: a disturbance occurs, the regulator narrows candidate responses, fixes a response class, emits a concrete response, and produces a closure through the Table of Outcomes. The information-theoretic formulation measures how much expected epistemic uncertainty is removed during that staged process.

A realized episode has an associated conditioning path: Y = y, U₁ = u₁, ..., U_k = u_k. The Knowledge Discovery Process is the staged reduction of conditional entropy H_{M_t}(X|Y) about the required response-equivalence class X . This entropy is the Knowledge To Be Discovered, measured in bits.

The organizing distinction is: the episode is the realized set-based regulatory event; the conditioning path is the information-theoretic path through that episode; the KTD quantities are expected uncertainty measures under the regulator's knowledge state; and the closure is the outcome-value produced after final response commitment.

Notation and Modeling Assumptions

In this subsection, D denotes the actual disturbance-value that enters the Table of Outcomes, while Y denotes the disturbance information available to the regulator. In the fully observed case, Y = D. In the partially observed case, Y may be a signal, observation, classification, or task condition that leaves several actual disturbance-values possible.

Unless otherwise stated, X denotes the required response-equivalence class at the regulatory granularity being analyzed. In the unique-target case, this is the variable previously denoted X_t^*. Thus X is not merely the regulator's actual response-class variation; it is the target response-class variable whose value must be fixed for successful regulation.

If several response-classes are equally acceptable, then uncertainty among those equally acceptable classes is not automatically Knowledge To Be Discovered. In that case, H(X|Y) should be interpreted as Knowledge To Be Discovered only if the model supplies a further selection criterion that turns the acceptable set into a target-class variable. Otherwise, residual uncertainty among equally acceptable response-classes is not regulatory ignorance at the granularity being analyzed.

The regulator's knowledge state is denoted by M_t. All probabilities, entropies, and mutual informations in this subsection are evaluated relative to the epistemic distribution induced by M_t. When that dependence matters, it is written explicitly as P_{M_t}, H_{M_t}, and I_{M_t}.

As in the set-based episode definition, the episode index t is fixed in this subsection. The response-equivalence map g_t : 𝓡 → 𝓧_t, the acceptable region η_t, and the knowledge state M_t are evaluated at the same episode index.

Role	Symbol	Meaning in this subsection
Actual disturbance	D	The disturbance-value that combines with the final concrete response in the Table of Outcomes.
Available disturbance information	Y	The observation, signal, classification, or task condition available to the regulator.
Required response-equivalence class	X	The response class still unresolved for the regulator after observing Y.
Knowledge state	M_t	The epistemic state relative to which probabilities, entropies, and mutual informations are evaluated.
Action unit	q_i	The operation performed at stage i.
Selection signal	U_i	The information-bearing result of action unit q_i.
Actually fixed response class	X̂_k	The response class selected by the regulator after k stages.
Concrete final response	R_final	A concrete response emitted from the fixed response class.
Closure	Z = T(D,R_final)	The outcome produced after final response commitment.

Staged Action Units and Realized Signals

An action unit is one operation performed inside a realized episode. It may be a test, observation, feedback step, available response-rule application, constraint, model application, or partial execution. The episode-level action-unit protocol is denoted by $Q_{t}$ . Its individual action units are denoted by $q_{t, i}$ . The observable result produced by action unit $q_{t, i}$ is denoted by $U_{t, i}$ . The result $U_{t, i}$ , not the mere occurrence of the action unit, is the information-bearing signal.

Within an episode indexed by $t$ , the external regulatory frame is fixed: the knowledge state is $M_{t}$ , the acceptable region is $η_{t}$ , and the realized disturbance-value is $d$ . The internal stages of the episode are indexed by $i = 1, \dots, k_{t}$ .

Let the action-unit prefix through stage $i$ be:

Q_{t, \leq i} := (q_{t, 1}, \dots, q_{t, i}) .

Let the corresponding realized signal prefix be:

U_{t, \leq i} := (U_{t, 1}, \dots, U_{t, i}) .

On a realized episode path, $Q_{t, \leq i} = q_{t, \leq i}$ and $U_{t, \leq i} = u_{t, \leq i}$ . The action-unit prefix specifies the staged procedure used by the regulator. The signal prefix gives the realized evidence generated by that procedure.

This avoids a conceptual conflation. The protocol $Q_{t}$ structures the episode. The action unit $q_{t, i}$ specifies a discriminating operation. The signal $U_{t, i}$ is the realized information-bearing result. The candidate-set update is the support-level consequence. Entropy reduction is the information-theoretic measure of how much uncertainty about the required response-equivalence class has been removed.

Expected Staged Reduction of Knowledge To Be Discovered

The initial Knowledge To Be Discovered is the regulator's remaining epistemic uncertainty, under $M_{t}$ , about which required response-equivalence class must be fixed after the available disturbance information $Y$ is known:

{KTD}_{t, 0} := H_{M_{t}} (X | Y) .

Each information-bearing signal U_i conditions that uncertainty further. After $i$ stages, the expected residual Knowledge To Be Discovered under the selected action-unit protocol is:

{KTD}_{t, i} := H_{M_{t}} (X | Y, Q_{t, \leq i} = q_{t, \leq i}, U_{t, \leq i}) .

The conditioning on the selected protocol makes explicit which action units were used. If the protocol is fixed in advance, or if it is a deterministic function of information already included in $Y$ and $M_{t}$ , then conditioning on $Q_{t, \leq i}$ is redundant and the shorter expression $H_{M_{t}} (X | Y, U_{t, \leq i})$ is recovered.

Equivalently, the residual Knowledge To Be Discovered after i stages is the initial Knowledge To Be Discovered minus the information gained from the first i selection signals:

{KTD}_{i} = H_{M_{t}} (X | Y) - I_{M_{t}} (X; U_{1}, \dots, U_{i} | Y) .

When the selected action unit at stage $i$ is treated as procedural context rather than new evidence, the expected reduction achieved by that stage is:

{KTD}_{t, i - 1} - {KTD}_{t, i} = I_{M_{t}} (X; U_{t, i} | Y, Q_{t, \leq i} = q_{t, \leq i}, U_{t, < i}) .

If the choice of the next action unit is itself informative about $X$ , then the selected action unit must be included in the information increment:

{KTD}_{t, i - 1} - {KTD}_{t, i} = I_{M_{t}} (X; Q_{t, i}, U_{t, i} | Y, Q_{t, < i}, U_{t, < i}) .

Over all stages, the total expected reduction is:

{KTD}_{t, 0} - {KTD}_{t, k_{t}} = I_{M_{t}} (X; U_{t, \leq k_{t}} | Y, Q_{t, \leq k_{t}} = q_{t, \leq k_{t}}) .

Shannon's chain rule for mutual information gives the operational decomposition of that total reduction:

I_{M_{t}} (X; U_{1}, \dots, U_{k} | Y) = \sum_{i = 1}^{k} I_{M_{t}} (X; U_{i} | Y, U_{< i}) .

The chain-rule identity holds regardless of dependence among the signals U₁, ..., U_k. It does not require the stage signals to be independent or conditionally independent. Dependence among stages is handled by conditioning each stage-wise term on the earlier signal-values.

Therefore the per-stage contributions must be conditional and incremental. If stages share information or impose overlapping constraints, summing their marginal reductions I(X;U_i|Y) can overcount. The chain-rule decomposition avoids that overcounting by crediting each stage only for the reduction of residual uncertainty left by previous stages.

Realized Conditioning Path Inside One Episode

The quantities KTD_i are expected conditional entropies under M_t. A realized episode, however, follows one concrete conditioning path: Y = y, U₁ = u₁, ..., U_k = u_k. After the signal-values are observed, the regulator's posterior uncertainty is represented by conditioning on those realized values.

For a realized episode, let the regulator's posterior distribution over required response-equivalence classes before stage i be:

p_{i - 1} (x) = P_{M_{t}} (X = x | Y = y, U_{< i} = u_{< i}) .

After observing U_i = u_i, the posterior becomes:

p_{i} (x) = P_{M_{t}} (X = x | Y = y, U_{\leq i} = u_{\leq i}) .

The realized entropy-based selection measure tracks the probability-weighted change in uncertainty:

σ_{i}^{ent} := H (p_{i - 1}) - H (p_{i}) .

In a realized episode, σ_i^ent may be positive, zero, or negative. It is positive when the observed signal concentrates probability mass, negative when the signal makes the posterior more diffuse, and zero when the entropy is unchanged. The non-negativity claim applies only in expectation.

For a fixed episode prefix Y = y, U_<i = u_<i, the conditional expectation of the realized entropy change is:

$𝔼 [σ_{i}^{ent} | Y = y, U_{< i} = u_{< i}] = I (X; U_{i} | Y = y, U_{< i} = u_{< i}) .$

Fully averaged over Y and the previous signal-values, this gives:

𝔼 [σ_{i}^{ent}] = I (X; U_{i} | Y, U_{< i}) .

At the terminal point of the realized conditioning path, the realized Knowledge To Be Discovered is the posterior entropy left after the actual signal-values have been observed:

${KTD}_{term}^{real} (y, q_{\leq k}, u_{\leq k}) := H_{M_{t}} (X ∣ Y = y, Q_{\leq k} = q_{\leq k}, U_{\leq k} = u_{\leq k}) .$

The realized reduction in Knowledge To Be Discovered along that path is therefore:

${ΔKTD}_{path}^{real} (y, q_{\leq k}, u_{\leq k}) := H_{M_{t}} (X | Y = y) - {KTD}_{term}^{real} (y, q_{\leq k}, u_{\leq k})$

In the unique-target case, if the realized conditioning path makes the required response-equivalence class posteriorly certain, then:

{KTD}_{term}^{real} (y, q_{\leq k}, u_{\leq k}) = 0 .

In that special case, the realized conditioning path has removed all of the initial Knowledge To Be Discovered for that episode:

{KTD}_{term}^{real} (y, q_{\leq k}, u_{\leq k}) = H_{M_{t}} (X | Y = y) .

This terminal quantity is still a posterior uncertainty measure, not yet a success condition. Zero terminal realized Knowledge To Be Discovered means that the required response-equivalence class has become identifiable under the model. Successful regulation additionally requires that the class actually fixed by the regulator be the required class.

If the selected action protocol $Q_{\leq k}$ is fixed in advance or is a deterministic function of information already contained in Y, then $H_{M_{t}} (X ∣ Y = y)$ In that special case, the expression using only $Y = y$ as the starting condition is recovered.

Expected Selection Induced by the Action Protocol

The realized path reduction above is path-specific. It measures how much posterior uncertainty has fallen after the particular signal-values

u_{\leq k}

have occurred. The below concerns the expected selection generated by the action protocol under the knowledge state

M_{t}

. For a fixed episode frame and fixed selected protocol

Q_{\leq k} = q_{\leq k},

define:

H_{M_{t}} (X ∣ Y = y, Q_{\leq k} = q_{\leq k}, U_{\leq k}) .

This term is an ordinary conditional entropy: it averages over the possible signal traces

U_{\leq k}

under

M_{t}

, conditional on

Y = y

and

Q_{\leq k} = q_{\leq k}

. Thus, realized path reduction and expected selection are related but not identical. The realized path quantity evaluates one observed path. The expected selection quantity measures the average uncertainty reduction produced by the staged action-unit protocol.

Bridge to the Set-Based Candidate Trace

The concrete staged trace and the entropy-based trace describe the same realized episode at two levels of description. The set-based trace records narrowing over concrete response-values $\emptyset \neq C_{k}^{R} (d) \subseteq \dots \subseteq C_{1}^{R} (d) \subseteq C_{0}^{R} (d) \subseteq R .$ The entropy-based trace records uncertainty over response-equivalence classes. To keep the levels distinct, let $C_{i}^{R} (d) \subseteq R$ denote the concrete candidate response-set after stage $i$ . Its response-class projection is $g_{t} [C_{i}^{R} (d)] \subseteq X_{t}$ .

Let $X_{t}$ be the response-class space under the knowledge state M_t, and let $g_{t} : R \to X_{t}$ map each concrete response-value to its response-equivalence class.

As in the set-based episode definition, the episode index t is fixed in this subsection. Therefore $C_{i} (d)$ abbreviates $C_{t, i} (d_{t})$ and the projected class-level candidate set $C_{i}^{X} (d)$ should be read as $C_{t, i}^{X} (d_{t})$ when the time index matters. The response-equivalence map $g_{t}$ , the acceptable region $η_{t}$ , and the knowledge state $M_{t}$ are all evaluated at the same episode index t.

Using the response-equivalence map g_t : 𝓡 → 𝓧_t defined above, any concrete candidate response-set $C_{i}^{R} (d) \subseteq 𝓡$ has an associated response-class projection: $C_{i}^{X} (d) := g_{t} [C_{i}^{R} (d)] = {g_{t} (r) : r \in C_{i}^{R} (d)}$

Thus, the set-based trace records narrowing over concrete response-values, while the entropy-based trace records narrowing over response-equivalence classes. They describe the same realized regulatory episode only relative to the chosen response-class abstraction g_t, and only when the probabilistic support over X_t is interpreted as the class-level projection of the concrete candidate trace.

For a realized episode, the associated conditioning path determines a sequence of posterior candidate response-class sets. After observing Y=y, U₁=u₁, ..., U_i=u_i, the information-theoretic trace defines the posterior candidate response-class set as:

C_{i}^{X} (y, u_{\leq i}) := supp (X | Y = y, U_{\leq i} = u_{\leq i}) .

In the present model, the set-based trace is assumed to realize the support-level effect of the conditioning path. Therefore, for the realized episode:

C_{i}^{X} (y, u_{\leq i}) . = g_{t} [C_{i}^{R} (d)]

This bridge condition says that a response-equivalence class remains possible after stage $i$ exactly when at least one concrete response in that class remains in the concrete candidate set, and the regulator's posterior under $M_{t}$ still assigns positive probability to that class.

Under the fixed response-equivalence abstraction g_t, the set-based and entropy-based traces describe the same realized regulatory episode at different levels of description: the former over concrete response-values, the latter over response-equivalence classes. The set-based formulation records the realized support-level narrowing. The information-theoretic formulation measures the expected reduction in the regulator's remaining epistemic uncertainty under M_t.

Lemma — Episode-Level Action-Unit Bridge

Within a closed episode t, the sequence of action units

Q_{\leq k}

gives the episode its internal staged structure. Each action unit

Q_{t,i}

specifies a discriminating operation; each realized signal

U_{t,i}

determines which candidates remain possible; and the resulting support-level trace i.e. the class-level candidate support induced by the realized action-unit history is:

C_{i}^{X} (d) := {supp}_{M_{t}} (X ∣ Y = y, Q_{\leq i} = q_{\leq i}, U_{\leq i} = u_{\leq i}) .

The concrete response trace and the entropy trace are connected by:

C_{i}^{X} (d) = g_{t} [C_{i}^{R} (d)]

Thus, the entropy-based candidate support after stage i is exactly the response-class projection of the concrete candidate response-set after stage i. Action units affect episodes by giving them their staged internal structure: $q_{i} \Rightarrow U_{i} \Rightarrow C_{i - 1}^{R} (d) \to C_{i}^{R} (d) .$ The action unit q_i specifies the discriminating operation performed at stage i. The realized signal u_i determines which concrete response-values remain compatible with the episode path. Projection through g_t then gives the remaining response-equivalence classes. If a realized signal has zero probability under the current knowledge state M_t, the event is not ordinary staged conditioning. It is a model-revision, reopening, or rework event and should be represented by an updated knowledge state M_t+ or by a new episode.

Bridge Lemma

For a fixed episode frame M_t, disturbance-value d, selected protocol

q_{\leq k}

, and realized signal path

u_{\leq k}

, suppose every conditioning event has positive probability under M_t, and suppose the bridge condition

C_{i}^{X} (d) = g_{t} [C_{i}^{R} (d)]

holds for every stage

i = 0, \dots, k

. Then the set-based staged trace and the entropy-based trace describe the same candidate-narrowing process at different levels of description. For finite discrete

X

, with

C_{k}^{X}

defined as the positive-probability posterior support:

{KTD}_{term}^{real} (y, q_{\leq k}, u_{\leq k}) := H_{M_{t}} (X ∣ Y = y, Q_{\leq k} = q_{\leq k}, U_{\leq k} = u_{\leq k}) = 0

if and only if the final class-level candidate support is a singleton:

C_{k}^{X} (d) = {x_{t}} .

If x_t is the acceptable response-equivalence class, then the episode has identified the required class. Successful regulation still requires that the committed concrete response-value r_t belong to the acceptable response-set

A_{t} (d)

Action Units, Signals, and Response-Class Commitment

An action unit may affect an episode in several distinct ways, which should not be conflated:

Case	Support effect	Probability effect	Interpretation
Pure support reduction	C_i^X ⊂ C_i-1^X	Relative probabilities among survivors are unchanged.	The signal rules out candidate response classes.
Probability redistribution only	C_i^X = C_i-1^X	p_i ≠ p_i-1	The same classes remain possible, but their probabilities change.
Mixed update	C_i^X ⊂ C_i-1^X	p_i ≠ p_i-1 on the surviving support.	The signal both eliminates classes and redistributes probability mass.
Epistemically null update	C_i^X = C_i-1^X	p_i = p_i-1	The signal contributes no information about the required response class.

In particular, support reduction and probability redistribution are not mutually exclusive: an informative signal may both eliminate some response classes and redistribute probability mass among the survivors.

First, the action unit may eliminate candidate response classes without otherwise changing the relative probability distribution among the surviving candidates. In that pure support-reduction case, the support strictly shrinks:

C_{i}^{X} \subset C_{i - 1}^{X} .

Second, the action unit may leave the candidate set unchanged while redistributing probability mass among the remaining candidates:

C_{i}^{X} = C_{i - 1}^{X}, p_{i} \neq p_{i - 1} .

In that case, the realized set-based selection measure is zero, because no response class has been ruled out:

σ_{i}^{set,X} = 0 .

However, the realized information-theoretic uncertainty σ_i^ent may still change because the probability distribution over the surviving candidates has changed.

Third, and most generally, the action unit may both eliminate candidate response classes and redistribute probability mass among the surviving candidates:

C_{i}^{X} \subset C_{i - 1}^{X}, p_{i} \neq p_{i - 1} on the surviving support.

In this mixed case, the realized set-based selection measure is positive because the support has shrunk:

σ_{i}^{set,X} > 0 .

The realized entropy-based selection measure σ_i^ent , however, may be positive, zero, or negative in a particular realized episode, depending on how the posterior probability mass is redistributed among the surviving candidates.

Fourth, the action unit may be epistemically null with respect to the required response-equivalence class. In that case, the posterior distribution is unchanged:

p_{i} = p_{i - 1} .

Therefore both the support and the entropy remain unchanged:

C_{i}^{X} = C_{i - 1}^{X}, σ_{i}^{ent} = 0 .

Thus, an action unit can narrow an episode by eliminating response classes, by concentrating probability mass among still-possible response classes, by doing both at once, or by contributing no information about the required response class at all. The set-based formulation observes support elimination. The information-theoretic formulation observes both support elimination and probability redistribution. This is why candidate-set reduction and entropy reduction are related but not identical.

σ_{i}^{set,X} := \log_{2} (\frac{| C_{i - 1}^{X} |}{| C_{i}^{X} |}) .

Note that this $σ_{i}^{set,X}$ is scored on the class-projected set $C_{i}^{X} (y, u_{\leq i}) . = g_{t} [C_{i}^{R} (d)]$ , and not on the concrete set $C_{i}^{R} (d)$ ; the two coincide only when $g_{t}$ is injective on the live survivors (no two surviving concrete responses share a class), and their difference on the surviving population is a source of calibration error. $ϵ_{c a l}$ .

The set-based formulation observes support elimination. The information-theoretic formulation observes both support elimination and probability redistribution. This is why candidate-set reduction and entropy reduction are related but not identical.

Under a fixed knowledge state M_t, ordinary conditioning cannot broaden the support of possible response classes, assuming the observed signal-value had positive probability under M_t. If an action unit reveals a prior candidate class that had zero prior support, then the event is not ordinary staged conditioning under M_t. It is a model revision, reopening, or rework event, and should be represented by an updated knowledge state M_t+ or by a new episode.

Action units affect episodes by giving them their staged internal structure:

q_{i} ⇝ U_{i} ⇝ C_{i - 1}^{R} \to C_{i}^{R} .

At some stage, the regulator has enough information to fix a response class. Let 𝓧_t be the set of response-equivalence classes over which X ranges. Let X̂_k ∈ 𝓧_t denote the response class actually fixed by the regulator after k stages of selection. This fixed class may be represented by a decision rule:

\hat{X_{k}} := δ_{k} (Y, U_{1}, \dots, U_{k}) .

This is distinct from X, which denotes the required response-class uncertainty being reduced by the staged-selection process. In a well-aligned successful case, the regulator fixes the response class required by the regulatory problem. But the notation keeps the required class and the actually fixed class separate, because a regulator may become confident and still fix the wrong class.

A good formal reading of the realized episode is:

$D = d \to Y = y \to q_{1} \to U_{1} = u_{1} \to \dots \to q_{k} \to U_{k} = u_{k} \to \hat{X_{k}} \to R_{final} \to Z = T (d, R_{final}) .$

This display still refers to the set-based episode. The sequence Y = y, U₁ = u₁, ..., U_k = u_k is the information-theoretic conditioning path associated with that episode.

This formulation assumes that the sequence of action units q₁, …, q_k is fixed in advance or generated by a policy already included in the regulator's prior structure M_t. If the choice of the next action unit is itself part of the selection process, then the selected action unit should also be included in the information sequence, for example as: $I_{M_{t}} (X; Q_{i}, U_{i} | Y, Q_{< i}, U_{< i}) .$

Success, Closure, and Policy-Level Success

At the response-class level, success requires that the actually fixed class lie inside the acceptable response-class set for the available disturbance information:

\hat{X_{k}} \in X_{acc, t} (Y) .

In the partially observed case, a response class is acceptable under Y = y only if every concrete response in that class is acceptable for every actual disturbance-value still possible under Y = y:

$X_{acc, t} (y) := {x \in X_{t} : \forall d \in supp (D | Y = y), x \subseteq A_{t} (d)} .$

This is a robust class-level acceptability condition. It is stronger than realized closure success, because it requires success for every disturbance still possible under the observation, not merely for the actual disturbance that occurs.

Once the response class is fixed, a concrete response is emitted from that class:

R_{final} \in \hat{X_{k}} .

The Table of Outcomes then produces the closure:

Z = T (D, R_{final}) .

Closure does not, by itself, imply that the terminal realized Knowledge To Be Discovered is zero. Closure means that the regulator has committed a final response and that the Table of Outcomes has produced an outcome-value. It does not necessarily mean that the realized conditioning path has eliminated all posterior uncertainty about the required response-equivalence class.

Z = T (D, R_{final}) ⇏ {KTD}_{term}^{real} (y, u_{\leq k}) = 0 .

A closed episode may therefore still end with positive terminal realized Knowledge To Be Discovered:

{KTD}_{term}^{real} (y, u_{\leq k}) > 0 .

This is not a contradiction. It means only that the episode has produced a closure while the model still represents residual uncertainty over the required response-equivalence class. Whether that residual uncertainty counts as remaining Knowledge To Be Discovered depends on the response-class granularity and on whether the model requires one specific target class to be fixed.

At the level of a realized episode, success is judged by the actual closure:

φ (T (d, r_{t})) \in η_{t} .

The closure is acceptable exactly when its induced essential-variable value lies in the acceptable region:

φ (Z) = φ (T (D, R_{final})) \in η_{t} .

At the probabilistic policy level, a stronger almost-sure success condition is:

\Pr (φ (T (D, R_{final})) \in η_{t}) = 1 .

These are different levels of evaluation. The first judges one realized episode. The second judges the regulator's policy across the modeled distribution of episodes.

In the unique-target case, successful selection requires that the residual uncertainty about the required response-equivalence class approach zero: H_{M_t}(X | Y, U₁, ..., U_k) → 0. However, zero residual entropy means only that the regulator has enough information to identify the required class. It does not by itself mean the regulator actually selects it. Successful selection additionally requires that the class actually fixed by the regulator equals the required class: X̂_k = X.

More generally, regulation does not require that only one concrete response remain possible. It requires that the concrete response finally emitted by the regulator belong to a response class that induces an outcome inside the acceptable region.

In the fully observed special case, where Y = D, the closure may also be written as Z = T(Y,R_final). In the general partially observed case, however, Y is only the regulator's observation or signal, while D is the actual disturbance-value that enters the Table of Outcomes.

Summary

The information-theoretic staged-selection formulation does not replace the Table of Outcomes, the outcome-to-essential-variable map, the acceptable region, the set-based episode, or the closure. It defines the Knowledge Discovery Process as the staged reduction of Knowledge To Be Discovered, relative to the regulator's knowledge state M_t.

The set-based episode is the realized regulatory event. The conditioning path is the information-theoretic path through that episode. The expected KTD trace measures staged uncertainty reduction before signal-values are known. The realized posterior trace records what happens after the actual signal-values are observed. The bridge condition links concrete candidate narrowing to response-class posterior support. Success is judged after final response commitment, when the emitted concrete response produces an acceptable closure.

In this limited formal sense, the Knowledge Discovery Process gives an “it from bit” reading of regulation: the realized response or response rule is the result of information-bearing selection from a larger space of possibilities[6].

Learning (across episodes in a window)

The preceding sections described how a single episode discovers enough information to commit a response and produce a closure. The present section asks a different question: whether the discoveries made inside one episode are retained as stored regulatory structure for later comparable episodes.

Comparable episodes

A comparable task class defines the reference frame for comparison. A comparable episode is a realized closed episode whose Knowledge To Be Discovered can be evaluated inside that reference frame. Comparability is therefore not an intrinsic property of an episode alone. It is a relation between an episode and a declared task class.

Let $τ_{j}$ denote a comparable task class. A comparable task class is not merely a collection of tasks that appear similar in ordinary language. It is a formal comparability frame for a recurring kind of regulatory problem. It fixes, or supplies explicit correspondences for, the disturbance-information variable $Y$ , the required response-equivalence variable $X$ , the response-equivalence abstraction $g : R \to X$ , and the modeling resolution at which Knowledge To Be Discovered is measured.

Thus, within a comparable task class, responses may differ at the concrete action level $R$ , but they are compared only after being projected into the same response-equivalence class space $X_{τ}$ . Likewise, disturbances may differ at the raw observational level, but they must be represented through the same disturbance-information variable $Y$ , or through an explicitly declared correspondence to it.

Comparability of task class therefore requires sameness of semantic structure: the same kind of disturbance information, the same kind of required response class, the same response-equivalence abstraction, and the same measurement resolution. It does not require the empirical probability distribution over $X$ or $Y$ to be identical across episodes. It means same regulatory measurement frame.

A closed episode $ε_{t}$ is comparable under $τ_{j}$ if the episode admits an interpretation in that task-class frame such that the following three quantities are well-defined over the same $X$ and $Y$ :

H_{t}^{start} := H_{M_{t}} (X | Y)

H_{t}^{term} := H_{M_{t}} (X | Y, U_{t})

H_{t + 1}^{start} := H_{M_{t + 1}} (X | Y) .

Two closed episodes $ε_{t}$ and $ε_{s}$ are comparable episodes when there exists a task class $τ_{j}$ such that both episodes are comparable under that same task class:

$ε_{t} \sim ε_{s} \Leftrightarrow \exists τ_{j} such that ε_{t} \in Ε_{τ_{j}} and ε_{s} \in Ε_{τ_{j}} .$

Here $Ε_{τ_{j}}$ is the class of closed episodes interpretable under task class $τ_{j}$ . The episodes may have different realized disturbances, different staged-selection paths, different committed responses, and different closure outcomes. They are comparable because the same response-selection uncertainty is being measured at the same abstraction level.

This means that all episodes assigned to $τ_{j}$ ask the same type of regulatory question: given a disturbance-information state, which response-equivalence class is required to keep the relevant outcome within the intended goal condition? In this sense, the same kind of regulatory problem is being solved.

For exact comparison, the following comparability conditions must hold:

the disturbance-information variable $Y$ has the same semantic meaning across the compared episodes;
the required response-equivalence variable $X$ has the same semantic meaning across the compared episodes;
the response-equivalence map $g$ is fixed, or its changes are mediated by an explicit equivalence between response classes;
the entropy quantities are evaluated at the same modeling resolution;
the marginal entropy of the required response-equivalence variable is held fixed when changes in stored coupling and changes in KTD are read as exact duals.

Thus comparable episodes are not episodes that look identical operationally. They are episodes whose Knowledge To Be Discovered is measured against the same unresolved response-selection problem.

In plain terms: two episodes do not need the same disturbance, response, outcome, duration, or internal number of stages. They need to belong to the same regulatory problem: "Given this kind of disturbance information, which kind of response-equivalence class must be fixed?"

Learning as stored transformation

Within an episode, staged selection reduces Knowledge To Be Discovered by conditioning on the available disturbance information and the subsequent selection signals. Across episodes, learning occurs only if some of that reduction is incorporated into the regulator's stored law of action, so that the next comparable episode begins with stronger disturbance-response coupling and less residual Knowledge To Be Discovered.

Thus, in this section, learning is the across-episode transformation:

M_{t} \to M_{t + 1}

where $M_{t}$ denotes the regulator's stored structural coupling at the start of episode $t$ . In Ashby's terms, this is the regulator's learned law of action: the stored functional or probabilistic structure by which disturbances are mapped to responses. It is not the Table of Outcomes itself.

The fixed environmental relation remains:

T : D \times R \to Z

and the outcome-to-essential-variable map remains:

φ : Z \to E

Learning does not alter $T$ or $φ$ in the fixed-table case. It alters the regulator's stored coupling $M_{t}$ , and therefore alters the response law induced at the start of later episodes.

From staged discovery to stored learning

For episode $t$ , let $M_{t}$ be fixed at the start of the episode. It induces the regulator's epistemic probability law over the required response-equivalence class:

P_{t} (X | Y) := P (X | Y; M_{t}) .

Here $X$ denotes the required response-equivalence class at the regulatory granularity being analyzed. In the unique-target case, this is the same variable previously denoted $X_{t}^{*}$ . Thus $X$ is not merely actual response variation. It is the target response-class variable whose value must be fixed for successful regulation under the adopted criterion.

The initial Knowledge To Be Discovered at the start of episode $t$ is:

H_{t} (X | Y) := H_{P_{t}} (X | Y) .

During the episode, the regulator observes an information-bearing sequence:

U_{t} := (U_{t, 1}, \dots, U_{t, k_{t}}) .

This is the within-episode evidence stream generated by the staged selection process. It may include tests, observations, feedback signals, constraint checks, partial executions, or other action-unit results. The corresponding within-episode posterior Knowledge To Be Discovered is:

H_{t} (X | Y, U_{t}) .

The within-episode discovery is the reduction:

H_{t} (X | Y) - H_{t} (X | Y, U_{t}) .

This reduction is not yet learning. It is only discovery inside the current episode. Learning occurs only if the regulator stores and reuses the resulting information by updating its law of action for later comparable episodes.

After the episode closes, the regulator may update its stored coupling using the evidence stream, the class it actually fixed, the final concrete response, the produced closure, and the valuation of that closure. Let the closure-valuation signal be:

v_{t} := 1_{{φ (Z_{t}) \in η_{t}}} .

Then a general update form is:

M_{t + 1} := Update (M_{t}, Y_{t}, U_{t}, \hat{X_{t, k_{t}}}, R_{final, t}, Z_{t}, v_{t}) .

This expression does not assume a particular memory mechanism. The update may overwrite, patch, strengthen, weaken, version, or reorganize the stored coupling. The formal question is not how storage is implemented, but whether the next induced response law has less residual Knowledge To Be Discovered for the same task class.

Across-episode comparison of stored coupling

In the across-episode analysis, the task class must be comparable. The stored coupling may change, but the response classes whose uncertainty is being measured must not silently change meaning.

Thus, for each episode $t$ , the stored coupling $M_{t}$ induces:

P_{t} (X | Y), H_{t} (X | Y), I_{t} (X; Y) .

Here $H_{t} (X | Y)$ is the residual lack of requisite knowledge at the start of episode $t$ . It measures how much uncertainty remains, after the available disturbance information is known, about which required response-equivalence class must be fixed.

The mutual information: $I_{t} (X; Y)$ is the stored requisite coupling at episode start: the amount of response-selection structure already aligned with the disturbance distinctions relevant to the task. It is an information-theoretic measure of the coupling induced by $M_{t}$ .

The comparability of episodes requires that both episodes be evaluated over the same task-class variables, alphabets, and abstraction maps. This makes the quantities $I (X; Y)$ and $H (X | Y)$ semantically comparable across episodes. However, semantic comparability alone does not require the marginal response-class variety $H (X)$ to remain constant, because two episodes can use the same response-class alphabet $X_{τ}$ while having different probability distributions over response classes. For example, both episodes may use the same response classes: $X_{τ} = {x_{1}, x_{2}, x_{3}, x_{4}}$ , but in one episode the required responses are evenly distributed, while in another one response class dominates. Same alphabet, different entropy.

For the narrower purpose of reading changes in stored requisite coupling $Δ_{t} I$ and changes in lack of requisite knowledge $H (X | Y)$ as exact duals, impose the stronger constant marginal response-variety assumption:

H_{t} (X) = H_{t + 1} (X) .

The assumption means that the marginal variety of required response classes has not changed between the two episodes.

Under this assumption, the identity $H (X) = I (X; Y) + H (X | Y)$ implies that any increase in stored requisite coupling is exactly matched by an equal decrease in lack of requisite knowledge.

Therefore, under the constant marginal response-variety assumption, an increase in stored requisite coupling is exactly equivalent to an equal decrease in residual lack of requisite knowledge:

Δ_{t} I = - Δ_{t} H (X | Y) .

If the constant marginal response-variety assumption is relaxed, the two changes need not coincide. Part of the change in mutual information may then come from drift in the marginal entropy $H_{t} (X)$ , not only from reduced conditional ignorance. In what follows, the constant marginal response-variety assumption is maintained.

Learning axiom

Learning Axiom (Structural Knowledge Accumulation). A regulator learns, in the structural-coupling sense, when the within-episode evidence stream is incorporated into an updated stored law of action such that the next comparable episode begins with less residual Knowledge To Be Discovered.

Formally, learning from episode $t$ to episode $t + 1$ requires:

H_{t + 1} (X | Y) < H_{t} (X | Y) .

Under the fixed marginal entropy assumption, this is equivalently:

I_{t + 1} (X; Y) > I_{t} (X; Y) .

In words: after the update, the regulator begins the next comparable episode with stronger stored disturbance-response coupling and therefore less residual uncertainty about which response-equivalence class must be fixed.

This axiom defines positive learning at the chosen regulatory granularity. If the update leaves $H_{t} (X | Y)$ unchanged, then the episode has not improved stored requisite knowledge for that task class. If the update increases the conditional entropy, the regulator has degraded its stored coupling.

This learning criterion is still epistemic. It says that the regulator has reduced uncertainty about the required response-equivalence class. Regulatory success also requires correctness: the class actually fixed by the regulator must be acceptable for the disturbance information and must produce an acceptable closure through the Table of Outcomes.

\hat{X_{k}} \in X_{acc, t} (Y)

and, after concrete response commitment:

φ (T (D, R_{final})) \in η_{t} .

Thus a regulator may learn in the epistemic sense and still fail if it stores or applies the wrong mapping. Conversely, a regulator may produce a successful closure once without learning, if the episode's discovery is not retained in $M_{t + 1}$ .

Strong learning: posterior becomes prior

The learning axiom above is weak. It requires only that the stored coupling improve. A stronger assumption is obtained when the regulator stores and reuses, without loss, the uncertainty reduction achieved inside episode $t$ .

Strong Learning Assumption (Posterior-Becomes-Prior Rule). For a stable task class, the posterior uncertainty achieved by the end of episode $t$ becomes the prior stored uncertainty at the start of the next comparable episode:

H_{t + 1} (X | Y) := H_{t} (X | Y, U_{t}) .

In words, the discoveries made during episode $t$ are not merely used once. They are incorporated into the stored structure that shapes the regulator's next prior response law.

Under the dual knowledge view, and under the invariant marginal entropy assumption, the same rule can be written as:

I_{t + 1} (X; Y) = H_{t} (X) - H_{t} (X | Y, U_{t}) .

This rule is not a consequence of conditioning alone. Conditioning happens inside the current episode. Learning requires retention: the posterior structure must be written into the regulator's stored law of action.

The Posterior-Becomes-Prior Rule therefore requires at least the following conditions:

the same task class or disturbance semantics across episodes;
the same response-equivalence map g_t : 𝓡 → 𝓧_t, or an explicit correspondence identifying the response classes across episodes;
successful retention of within-episode discoveries;
reuse of the retained structure in later episodes;
no intervening forgetting, context drift, or criterion change that invalidates the comparison.

Corollary (Complete Adaptation under Strong Learning). Under repeated successful strong learning, the stored requisite coupling approaches its task-class ceiling:

I_{t} (X; Y) \to H (X)

and the residual lack of requisite knowledge approaches zero:

H_{t} (X | Y) \to 0 .

In that limit, no further within-episode discovery is required to determine the response-equivalence class for the task class under study. $H_{t} (X | Y) = 0$ This is complete adaptation at the chosen regulatory granularity.

Learning, goal revision, and behavioral revision

Learning must be distinguished from goal revision and behavioral revision. They modify different parts of the regulatory model.

Goal revision changes the acceptable essential-variable region:

η_{t_{1}} \to η_{t_{2}}

and therefore changes the acceptable outcome-set:

O_{acc, t_{1}} \to O_{acc, t_{2}} .

Behavioral revision changes what the regulator does. At the rule level, this means a change in the response rule:

ρ_{t_{1}} \to ρ_{t_{2}} .

Learning changes the stored law of action:

M_{t} \to M_{t + 1} .

These changes may be related, but they are not identical. A criterion can change without learning. A behavior can change without learning if the regulator merely switches among already available rules. A regulator can learn without immediately producing a different outcome if the newly stored structure is not yet exercised in a later episode.

This distinction is important for the fixed-table case. Outcome-values are not deleted from $T$ . They may lose or gain acceptability because $η_{t}$ changes. But learning is not the change in acceptability itself. Learning is the change in stored coupling that improves later response selection under the task class being compared.

Knowledge Discovery Accounting

Operational ledger

Let the fixed regulatory frame be the Table of Outcomes:

T : D \times R \to Z

with outcome-to-essential-variable map

φ : Z \to E

At time $t$ , the acceptable essential-variable region is

η_{t} \subseteq E

This induces the acceptable outcome-set:

O_{acc, t} := φ^{- 1} [η_{t}] = {z \in Z : φ (z) \in η_{t}}

Closure events

A closure event at time $u$ is an act in which the regulator selects a response $r_{u} \in R$ against an observed disturbance $d_{u} \in D$ , producing the realized outcome-value:

z_{u} := T (d_{u}, r_{u}) .

When the closure event is generated by the response rule prevailing at time u, we have $r_{u} = ρ_{u} (d_{u})$ . The ledger can also be read more generally as recording realized response selections, even when no total response rule is reconstructed.

The closure event is recorded as:

c_{u} = (u, d_{u}, r_{u}, z_{u}) .

It is an acceptable closure when produced iff:

z_{u} \in O_{acc, u}

Equivalently:

φ (z_{u}) \in η_{u} .

Thus an acceptable closure is not merely an outcome-value in the table. It is a realized action whose produced outcome was acceptable under the criterion prevailing at the time of production.

Window

Let the observation window be:

I = (t_{a}, t_{b}] .

The window contains the closure events whose event times fall inside the interval. Using a half-open interval avoids double-counting events at boundaries when consecutive windows are used.

Define the accepted closure history inside the window:

C_{I}^{+} := (c_{u} : t_{a} < u \leq t_{b}, z_{u} \in O_{acc, u}) .

This is an event history, not a set of outcome-values. Therefore it preserves multiplicity. If two different closure events produce the same outcome-value,

z_{u} = z_{v}, u \neq v,

they still count as two closure-fixing acts.

Gross counted closures

The gross counted closures in the window are:

S_{gross} (I) := | C_{I}^{+} | .

This counts all successful-at-production closure-fixing acts in the window. It does not count failed attempts. If an action produced an outcome that was not acceptable under the criterion prevailing at the time of production, $z_{u} \notin O_{acc, u}$ , then it does not enter $C_{I}^{+}$ , because the ledger is tracking cases of successful regulation that may later cease to count under revised success criteria.

Historically realized outcome-set

The historically realized outcome-set induced by the accepted closure history is only the support of the trace:

O_{I}^{r, +} := {z_{u} : c_{u} \in C_{I}^{+}} \subseteq Z .

Because this is a set, it collapses duplicates. Thus:

| O_{I}^{r, +} | \leq S_{gross} (I) .

The inequality may be strict when multiple acceptable closure events produce the same outcome-value. Therefore $O_{I}^{r, +}$ answers: which acceptable outcome-values appeared? By contrast, $S_{gross} (I)$ answers: how many acceptable closure-fixing acts were expended?

Continuously surviving counted closures through the window

The operational section evaluates originally successful closures over the criterion history of the window, not merely against the final criterion. A closure event $c_{u} \in C_{I}^{+}$ was successful when produced. It counts as a surviving closure at the end of the window only if its produced outcome-value was never invalidated by any acceptability criterion that applied after its production time.

Thus a closure event $c_{u}$ survives the window iff:

\forall t \in [u, t_{b}], z_{u} \in O_{acc, t} .

Define the surviving counted closures in the window as:

$S_{surv} (I) := # {c_{u} \in C_{I}^{+} : \forall t \in [u, t_{b}], z_{u} \in O_{acc, t}} .$

Equivalently:

S_{surv} (I) = \sum_{c_{u} \in C_{I}^{+}} 1_{{\forall t \in [u, t_{b}], z_{u} \in O_{acc, t}}} .

This is a survival-through-the-window count. It asks how many closures were successful when produced and were never invalidated by any acceptability criterion applied from their production time through the end of the window. It is therefore a continuous-survival count, not merely a final-criterion count.

Invalidation load

Define history invalidation load in the window as the number of originally successful closures that were later invalidated by at least one acceptability criterion before the end of the window:

W (I) := # {c_{u} \in C_{I}^{+} : \exists t \in [u, t_{b}], z_{u} \notin O_{acc, t}} .

Equivalently:

W (I) = \sum_{c_{u} \in C_{I}^{+}} 1_{{\exists t \in [u, t_{b}], z_{u} \notin O_{acc, t}}} .

Thus $W (I)$ counts closure-fixing acts that were successful when produced but failed to survive the subsequent criterion history of the window. It does not count the corrective work that replaces them.

Therefore:

S_{gross} (I) = S_{surv} (I) + W (I) .

Hence:

S_{surv} (I) = S_{gross} (I) - W (I) .

Interpretation

The ledger separates four levels:

possible outcome-values in $Z$ ;
the time-indexed criterion of acceptability $O_{acc, t}$ ;
realized closure events in the temporal trace;
closure events that remained continuously accepted through the rest of the window.

Ashby's table $T$ remains fixed. Outcome-values are not deleted from $T$ . What changes over time is the criterion by which fixed outcome-values are judged acceptable:

O_{acc, t} := φ^{- 1} [η_{t}] .

This distinction matters. A criterion revision is a change in the acceptable region, and therefore in the acceptable outcome-set:

O_{acc, t_{1}} \neq O_{acc, t_{2}} .

A behavioral revision, by contrast, is a change in what the regulator actually does. At the rule level, this means a change from one response rule to another:

ρ_{t_{1}} \neq ρ_{t_{2}}

and, at the induced-outcome level, it means a change in the rule-induced outcome map or in its image:

y_{t_{1}} [D] \neq y_{t_{2}} [D] .

The operational ledger in this section tracks criterion invalidation of already successful closures. It does not, by itself, prove that the regulator has changed its behavior. A closure can therefore be successful when produced and later cease to count because the goal criterion changes:

z_{u} \in O_{acc, u} but z_{u} \notin O_{acc, t_{b}} .

That is the operational meaning of $W (I)$ in this ledger. More generally, $W (I)$ counts closures that were successful when produced but were invalidated at least once before the end of the window, even if they later became acceptable again.

$W (I)$ measures invalidated successful closure, not completed corrective rework. Corrective rework is observed only when a later closure event, response selection, or response-rule revision replaces or repairs the invalidated closure.

Corrective rework would require an additional behavioral event: the regulator must select a new response, produce a new outcome-value, or revise the response rule so that the revised behavior again satisfies the current acceptable outcome-set. That would be tracked by comparing the produced closure history or the response rules before and after the criterion revision, not merely by comparing $O_{acc, u}$ with $O_{acc, t_{b}}$ .

Therefore, this ledger does not model deletion of outcome-values from $T$ , and it does not yet model all behavioral replacement work. It models the narrower case in which a previously successful closure is invalidated by a later criterion of success. Behavioral revision is a separate question: it begins only when the regulator changes what it produces in response to disturbances.

Operational ledger for goal-model revision

The ledger above tracks the case in which a single time-indexed acceptable set $O_{acc, t}$ serves both as the criterion under which closures are produced and as the criterion against which they are later evaluated. A closure can be invalidated only by external goal revision, i.e. by a change in $η_{t}$ itself.

A parallel case arises when the regulator does not know the acceptable region perfectly. The regulator acts under a believed acceptable region, while survival is judged against an authoritative acceptable region. In that case, invalidation is driven not by external goal revision but by revision of the regulator's model of the goal.

In this case, there are two acceptability structures:

the authoritative acceptable outcome-set, which remains fixed during the window;
the regulator's believed acceptable outcome-set, which may change as knowledge is discovered.

Authoritative and believed acceptability

Let the authoritative acceptable essential-variable region be:

η^{*} \subseteq E .

The authoritative acceptable outcome-set is its pullback along $φ$ :

O^{*} := φ^{- 1} [η^{*}] = {z \in Z : φ (z) \in η^{*}} .

The authoritative set $O^{*}$ does not change during the knowledge-discovery process. What changes is the regulator's believed model of the acceptable region.

At time $t$ , let the regulator's believed acceptable essential-variable region be:

\hat{η}_{t} \subseteq E

This induces the regulator's believed acceptable outcome-set:

\hat{O}_{t} := φ^{- 1} [{\hat{η}}_{t}] \subseteq Z .

Thus, in goal-model revision, the operative distinction is not:

O_{acc, t_{1}} \neq O_{acc, t_{2}}

but rather:

\hat{O}_{t_{1}} \neq \hat{O}_{t_{2}} while O^{*} remains fixed.

This is why the process is called goal-model revision, not external goal revision. The goal did not change. The regulator's model of the goal changed.

The believed acceptable set may be incorrect: in general,

{\hat{O}}_{t} \neq O^{*} .

The believed set may include outcome-values that the authoritative set excludes, exclude outcome-values that the authoritative set includes, or both.

Provisional closure events

A closure event at time $u$ is still recorded as:

c_{u} = (u, d_{u}, r_{u}, z_{u})

But in a goal-model-revision process, the closure is not yet judged by the authoritative set. It is provisionally accepted when produced iff the produced outcome-value belongs to the regulator's believed acceptable set at that time:

z_{u} \in \hat{O}_{u} .

Equivalently:

φ (z_{u}) \in {\hat{η}}_{u} .

A provisionally accepted closure is not necessarily an authoritatively acceptable closure. It is a closure that the regulator's model of the goal admits at the time of production.

Thus provisional acceptability is model-relative. It records what the regulator counted as successful under its current believed goal model.

Provisional closure history

Let the observation window be:

I = (t_{a}, t_{b}] .

The provisional closure history in the window is:

{\hat{C}}_{I}^{+} := (c_{u} : t_{a} < u \leq t_{b}, z_{u} \in \hat{O}_{u}) .

This is an event history, not a set of outcome-values. It preserves multiplicity. If the regulator produces several provisional closures for the same target position, all of those closure-fixing acts remain visible in the ledger.

Gross provisional closures

The gross provisional closures in the window are:

S_{gross}^{\hat{}} (I) := | {\hat{C}}_{I}^{+} | .

This counts all closure-fixing acts that were provisionally accepted under the regulator's believed model at the time of production.It does not yet say whether those closures were authoritative successes.

Net surviving closures

A provisionally accepted closure survives authoritative checking iff its produced outcome-value belongs to the fixed authoritative acceptable outcome-set:

z_{u} \in O^{*} .

Equivalently:

φ (z_{u}) \in η^{*} .

Define the authoritative net surviving closures in the window as:

S_{net} (I) := # {c_{u} \in {\hat{C}}_{I}^{+} : z_{u} \in O^{*}} .

This counts closure-fixing acts that were provisionally accepted when produced and were authoritatively acceptable.

Unlike the external goal-revision ledger, this survival test does not require a time-indexed criterion history after production. The authoritative acceptable set is fixed. The change is epistemic: the regulator later discovers whether a provisional closure was inside or outside the authoritative set all along.

Goal-model invalidation load

A provisionally accepted closure is invalidated by goal-model revision iff it was accepted under the believed model when produced but is outside the fixed authoritative acceptable outcome-set:

z_{u} \in \hat{O}_{u} but z_{u} \notin O^{*} .

Define the goal-model invalidation load in the window as:

W_{model} (I) := # {c_{u} \in {\hat{C}}_{I}^{+} : z_{u} \notin O^{*}} .

This counts closure-fixing acts that were successful relative to the regulator's believed model at production time, but failed the authoritative check. $W_{model} (I)$ measures invalidated provisional closures, not completed corrective rework. Corrective rework is observed only when a later closure event or response-rule revision replaces or repairs the invalidated closure.

Ledger identity

Every provisional closure either survives authoritative checking or is invalidated by it. Therefore:

S_{gross}^{\hat{}} (I) = S_{net} (I) + W_{model} (I) .

Hence:

S_{net} (I) = S_{gross}^{\hat{}} (I) - W_{model} (I) .

This identity is not an entropy identity. It is an operational accounting identity: provisional closure work equals authoritative surviving closure work plus model-invalidation load.

Model-revision events

If the model updates themselves need to be represented explicitly, introduce a model-revision event:

m_{v} = (v, M_{v^{-}}, M_{v}, \hat{O}_{v^{-}}, \hat{O}_{v}, q_{v}) .

Here $M_{v^{-}}$ is the model before revision, $M_{v}$ is the model after revision, and $q_{v}$ is the checking evidence, observation, comparison, or authoritative feedback that triggered the revision.

The model-revision event induces believed loss and gain sets:

{\hat{L}}_{v} := \hat{O}_{v^{-}} ∖ \hat{O}_{v} .

{\hat{G}}_{v} := \hat{O}_{v} ∖ \hat{O}_{v^{-}} .

A prior provisional closure $c_{u}$ is invalidated by the model-revision event $m_{v}$ if the closure occurred before the model revision and its outcome-value is among the values removed from the believed acceptable set:

u < v and z_{u} \in {\hat{L}}_{v} .

In the special case where the revision is caused by authoritative checking, the removed believed values are precisely those discovered not to belong to the authoritative acceptable set:

z_{u} \in {\hat{L}}_{v} \Rightarrow z_{u} \notin O^{*} .

This makes the knowledge-discovery structure explicit: the regulator acts under a believed goal model, receives evidence, revises the model, and thereby invalidates some earlier provisional closures.

Corrective replacement

Goal-model invalidation does not, by itself, prove that corrective replacement has occurred. Corrective replacement requires a later closure event, response selection, or response-rule revision that repairs the invalidated closure.

If needed, this can be represented by an additional repair relation $κ$ between closure events:

κ (c_{u}, c_{v})

where $κ (c_{u}, c_{v})$ means that the later closure $c_{v}$ is treated as a corrective replacement for the earlier invalidated closure $c_{u}$ . At minimum, such a relation should satisfy:

$κ (c_{u}, c_{v}) \Rightarrow u < v and z_{u} \notin O^{*} and z_{v} \in O^{*} .$

In the typing example, a natural repair relation may also require that both closure events address the same target position:

κ (c_{u}, c_{v}) \Rightarrow p_{u} = p_{v} .

The repair relation is additional structure. The invalidation ledger can count model-invalidation load without it. The repair relation is needed only when the modeler wants to identify which later closure repaired which earlier provisional closure.

Relation to the criterion-revision ledger

The criterion-revision ledger and the goal-model-revision ledger are two instances of the same accounting structure, separated by which acceptable set plays the role of production criterion and which plays the role of evaluation criterion.

In the criterion-revision ledger, both roles are played by the same time-indexed acceptable set $O_{acc, t}$ . A closure is acceptable when produced iff $z_{u} \in O_{acc, u}$ , and it survives iff it remains in $O_{acc, t}$ for every $t \in [u, t_{b}]$ . Invalidation is then driven by external goal revision.

In the goal-model-revision ledger, the production criterion is the believed acceptable set ${\hat{O}}_{u}$ , while the evaluation criterion is the authoritative acceptable set $O^{*}$ . Invalidation is then driven by revision of the regulator's model of the goal, not by any change in the authoritative goal itself.

The two ledgers coincide in the degenerate case in which the regulator's believed model agrees at all times with the authoritative criterion, that is, ${\hat{O}}_{t} = O^{*}$ for all $t$ in the window, and the authoritative criterion is itself constant. In that degenerate case, $W_{model} (I) = 0$ and $S_{net} (I) = S_{gross}^{\hat{}} (I)$ .

In general, the two ledgers answer different questions. $W (I)$ measures invalidation by criterion change. $W_{model} (I)$ measures invalidation by model mismatch under a fixed authoritative criterion. Neither measures corrective rework: corrective rework is a separate behavioral event tracked by changes in the response rule or in subsequent closure events.

The example in the next section instantiates the goal-model-revision ledger for a typing task in which the authoritative goal is fixed throughout, and the invalidation load $W_{model} (I)$ records the discovery process by which the typist's believed model ${\hat{O}}_{t}$ is brought into agreement with the authoritative criterion $O^{*}$ .

Interpretation

This ledger separates three things that should not be collapsed:

provisional closure: the regulator produced an outcome accepted by its believed goal model;
model invalidation: later checking showed that some provisional closures were outside the authoritative acceptable set;
corrective replacement: later behavior repaired the invalidated closure.

Thus the goal-model-revision ledger does not say that the authoritative goal changed. It says that the regulator discovered that its believed model of the goal was wrong or incomplete. The authoritative acceptable set remained fixed, while the believed acceptable set was revised.

That is the operational form of a human knowledge-discovery process: provisional closure under an imperfect model, discovery of mismatch against the authoritative goal, invalidation of some earlier closures, and possible corrective replacement.

Operational counting of action units as Effective non-net-progress load

Observable invalidation load enters through the operational ledger. Some gross closure events are counted when produced but later fail to survive the window's evaluation criterion. In the external criterion-revision ledger, this invalidation load is $W (I)$ . In the goal-model-revision ledger, the corresponding invalidation load is $W_{model} (I)$ .

The episode-level protocol $Q_{t}$ records the ordered sequence of action units used inside episode $t$ . However, not every internal action unit is counted in the operational ledger. Some action units may be coordination, setup, emission, closure, bookkeeping, or rework rather than non-closure discrimination. The operational count therefore uses a counting indicator.

Let $χ_{eff}$ be the indicator that an action unit is counted as an effective non-closure discrimination unit:

χ_{eff} (q_{t, i}) := {\begin{cases} 1 & if q_{t, i} is counted as an effective non-closure discrimination unit, \\ 0 & otherwise. \end{cases}}

For a window of closed episodes $I$ , the gross action-unit count is:

Q (I) := \sum_{t \in I}^{} \sum_{i = 1}^{k_{t}} χ_{eff} (q_{t, i}) .

Definition (Effective non-net-progress load). If the measurement window records observed invalidation load or lost non-closure discrimination as $W_{obs} (I)$ , then the effective non-net-progress load in window $I$ is:

Q_{eff} (I) := Q (I) + W obs (I) .

This is an operational ledger quantity. It counts effective discriminating work at the observed action-unit level. It is the physical non-closure count $Q (I)$ augmented by a one-unit non-progress debit for each invalidated gross closure. By construction $Q_{eff} (I) \geq Q (I)$ , with equality if and only if $W_{obs} (I) = 0$ ; whenever invalidation occurs,

Combining the definition with $S_{net} = S_{gross} - W_{obs}$ :

Q_{eff} (I) + S_{net} (I) = (Q + W_{obs}) + (S_{gross} - W_{obs}) = Q + S_{gross}

In the physical partition, each invalidated closure sits on the closure side, inside $S_{gross} (I)$ . In the effective partition, that same closure has been removed from the surviving-closure side — it is not in $S_{net} (I)$ — and re-booked as a non-progress debit inside $Q_{eff} (I)$ . No new units are introduced; the invalidated closures are simply re-attributed from “closure” to “load.” Equivalently, relative to the physical channel each invalidated closure is counted twice across the two partitions: once as the gross-closure unit it physically is, and once as the discrimination-equivalent debit it is charged to. This double appearance across partitions — not within either one — is precisely why $Q_{eff}$ is a defined effective load and not a action unit count.

Knowledge ledger

The operational ledger records realized closure events. The knowledge ledger attaches a bit-valued epistemic accounting row to each closure event. It answers a different question: after a closure and its associated update, how much Knowledge To Be Discovered remains for the next comparable episode?

The operational ledger counts closure-fixing acts. The knowledge ledger counts changes in residual Knowledge To Be Discovered. Therefore the two ledgers are linked by the same closure history, but they do not measure the same quantity.

Closure-indexed knowledge ledger

Let the operational closure event at episode index $t$ be:

c_{t} = (t, d_{t}, r_{t}, z_{t}) .

Let $τ_{t}$ denote the comparable task class under which the episode is evaluated. The task class fixes the meaning of the disturbance information $Y$ , the required response-equivalence variable $X$ , and the response-equivalence map used for comparison across episodes.

The closure-indexed knowledge ledger row is:

$k_{t} := (c_{t}, τ_{t}, M_{t}, M_{t + 1}, H_{t}^{start}, H_{t}^{term}, H_{t + 1}^{start}, B_{t}^{disc}, G_{t}^{K}, L_{t}^{K}) .$

This row records the epistemic state before the episode, the terminal posterior uncertainty reached inside the episode, and the stored uncertainty with which the next comparable episode begins.

KTD states at closure boundaries

The initial Knowledge To Be Discovered at the start of episode $t$ is:

H_{t}^{start} := H_{M_{t}} (X | Y) .

This is the residual lack of requisite knowledge induced by the stored law of action $M_{t}$ before the episode's internal staged selection has occurred.

Let the episode's information-bearing evidence stream be:

U_{t} := (U_{t, 1}, \dots, U_{t, k_{t}}) .

The terminal Knowledge To Be Discovered inside the episode is:

H_{t}^{term} := H_{M_{t}} (X | Y, U_{t}) .

This quantity is evaluated under the knowledge state that governed the episode. It measures posterior uncertainty after the episode's actual evidence stream has been observed. It does not yet say how much of that discovery has been retained.

The stored Knowledge To Be Discovered at the start of the next comparable episode is:

H_{t + 1}^{start} := H_{M_{t + 1}} (X | Y) .

This is the key knowledge-ledger balance after closure and update. It measures how much Knowledge To Be Discovered remains in the stored law of action for the next comparable episode.

Within-episode discovery and retained learning

The within-episode discovery achieved by the staged selection process is:

B_{t}^{disc} := H_{t}^{start} - H_{t}^{term} .

This is discovery inside the episode. It is not yet stored learning. Stored learning is measured by comparing the start of the current episode with the start of the next comparable episode.

The retained KTD reduction is:

G_{t}^{K} := \max (H_{t}^{start} - H_{t + 1}^{start}, 0) .

This is the knowledge gain recorded by the ledger. It counts the number of bits by which the next comparable episode begins with less Knowledge To Be Discovered.

The KTD increase is:

L_{t}^{K} := \max (H_{t + 1}^{start} - H_{t}^{start}, 0) .

This is the knowledge loss recorded by the ledger. It counts the number of bits by which the next comparable episode begins with more Knowledge To Be Discovered. That may occur through forgetting, model drift, criterion misalignment, incorrect generalization, or degradation of stored coupling.

Knowledge ledger stock-flow identity

The knowledge ledger has the following exact stock-flow identity:

H_{t + 1}^{start} = H_{t}^{start} - G_{t}^{K} + L_{t}^{K} .

This identity says that the next episode's initial Knowledge To Be Discovered equals the current episode's initial Knowledge To Be Discovered, minus retained knowledge gain, plus knowledge loss.

Equivalently, in stored-coupling form under the comparability assumption:

I_{t + 1}^{start} = I_{t}^{start} + G_{t}^{K} - L_{t}^{K} .

The KTD form and the stored-coupling form are dual readings of the same update when the task class, disturbance-information semantics, response-equivalence map, and marginal entropy of the required response-equivalence class are comparable across episodes.

Relation to the operational ledger

The operational ledger and the knowledge ledger are joined by the closure event $c_{t}$ . The same closure can be read operationally as a produced outcome and epistemically as a boundary at which Knowledge To Be Discovered is measured.

Ledger	Recorded unit	Primary measure	Question answered
Operational ledger	Closure event	Count of closure-fixing acts	What was produced, preserved, or invalidated?
Knowledge ledger	Closure-indexed KTD state	Bits of residual Knowledge To Be Discovered	Did the next comparable episode begin with less KTD?

The operational ledger identity:

S_{gross} (I) = S_{surv} (I) + W (I)

is an accounting identity over closure counts. The knowledge ledger identity:

H_{t + 1}^{start} = H_{t}^{start} - G_{t}^{K} + L_{t}^{K}

is an accounting identity over bits of Knowledge To Be Discovered. The two identities should not be conflated.

An invalidated closure may trigger learning, but invalidation is not itself learning. A corrective closure may show changed behavior, but changed behavior is not itself stored learning. Stored learning is demonstrated only when the next comparable episode begins with less residual Knowledge To Be Discovered:

H_{t + 1}^{start} < H_{t}^{start} .

Interpretation

The closure-indexed knowledge ledger separates four quantities that are often confused:

Within-episode discovery: the reduction from $H_{t}^{start}$ to $H_{t}^{term}$ inside the episode.
Retained learning: the reduction from $H_{t}^{start}$ to $H_{t + 1}^{start}$ across episodes.
Knowledge loss: any increase in the next episode's starting Knowledge To Be Discovered.
Operational invalidation: a closure-count event in the operational ledger, not automatically a bit-valued knowledge loss.

Thus, a closure can be operationally successful but epistemically weak if it does not reduce future Knowledge To Be Discovered. A closure can involve rework and still produce positive learning if the next comparable episode begins with stronger stored coupling. Conversely, a closure can be accepted and still produce no learning if the discovered information is not retained.

The knowledge ledger therefore gives the operational ledger its epistemic counterpart: the operational ledger records what the regulator produced; the knowledge ledger records how much ignorance the regulator still carries forward.

Window-level accounting measures

So far, we have presented how the operational and knowledge ledgers are populated at the level of closure events and closure-indexed knowledge rows over an episode. For measurement purposes, those rows can also be aggregated over an observation window. Window-level accounting measures do not introduce new regulatory dynamics. They summarize the operational and epistemic traces already recorded by the ledgers.

The central measurement question is: over a given window and task class, how much residual Knowledge To Be Discovered did episodes begin with, on average? This section defines that quantity as an average of per-episode residual ignorances. It is not the entropy of a pooled variable, and it is not a new information-theoretic identity.

Measurement window and eligible knowledge rows

Let the observation window be:

I = (t_{a}, t_{b}] .

The window contains closure-indexed knowledge-ledger rows whose closure times fall inside the interval. As in the operational ledger, the half-open interval avoids double-counting boundary events when consecutive windows are used.

For a comparable task class $τ_{j}$ , define the eligible knowledge-row history in the window as:

K_{I, τ_{j}} := (k_{u} : t_{a} < u \leq t_{b}, τ_{u} = τ_{j}) .

This is an event history, not a set of unique task types. It preserves multiplicity: if several closure events in the same task class occur inside the window, each contributes one row.

Let the number of eligible rows be:

n_{I, τ_{j}} := | K_{I, τ_{j}} | .

If $n_{I, τ_{j}} = 0$ , the task-class-specific window measures below are undefined for that window.

Average starting Knowledge To Be Discovered

For each eligible row $k_{u}$ , define the pre-episode residual ignorance as the row's starting Knowledge To Be Discovered:

H_{pre} (u) := H_{u}^{start} = H_{M_{u}} (X | Y) .

The task-class-specific average Knowledge To Be Discovered in the window is:

{KTD}_{avg}^{τ_{j}} (I) := \frac{1}{n_{I, τ_{j}}} \cdot \sum_{k_{u} \in K_{I, τ_{j}}}^{} H_{pre} (u) .

This is an average of per-episode residual ignorances. It answers: among the comparable episodes that closed inside the window, how much response-selection uncertainty did the regulator still carry at episode start, on average?

The same statistic can be evaluated over all task classes by omitting the task-class restriction:

$K_{I} := (k_{u} : t_{a} < u \leq t_{b}), {KTD}_{avg}^{all} (I) := \frac{1}{| K_{I} |} \cdot \sum_{k_{u} \in K_{I}} H_{pre} (u) .$

The all-task-class version is useful as an overall operational dashboard measure. The task-class-specific version is usually more interpretable, because Knowledge To Be Discovered is meaningful only relative to a declared comparability frame.

Companion window knowledge measures

The same eligible knowledge-row history can be used to compute companion averages. The average terminal Knowledge To Be Discovered is:

{KTD}_{term-avg}^{τ_{j}} (I) := \frac{1}{n_{I, τ_{j}}} \cdot \sum_{k_{u} \in K_{I, τ_{j}}} H_{u}^{term} .

The average within-episode discovery is:

B_{avg}^{disc, τ_{j}} (I) := \frac{1}{n_{I, τ_{j}}} \cdot \sum_{k_{u} \in K_{I, τ_{j}}} B_{u}^{disc} .

The average retained knowledge gain is:

G_{avg}^{K, τ_{j}} (I) := \frac{1}{n_{I, τ_{j}}} \cdot \sum_{k_{u} \in K_{I, τ_{j}}} G_{u}^{K} .

The average knowledge loss is:

L_{avg}^{K, τ_{j}} (I) := \frac{1}{n_{I, τ_{j}}} \cdot \sum_{k_{u} \in K_{I, τ_{j}}} L_{u}^{K} .

Finally, the average retained KTD reduction is:

R_{avg}^{K, τ_{j}} (I) := G_{avg}^{K, τ_{j}} (I) - L_{avg}^{K, τ_{j}} (I) .

This quantity is positive when the average ledger row records net retained reduction in future Knowledge To Be Discovered. It is negative when knowledge loss dominates retained gain.

Relation to operational window measures

The operational ledger and the knowledge ledger are joined by the closure-event index. The operational ledger classifies closure events by their operational status: produced, surviving, invalidated, provisionally accepted, or authoritatively accepted. The knowledge ledger attaches bit-valued epistemic quantities to those same closure events.

This join supports measurement queries that neither ledger answers in isolation. The operational ledger alone can say which closures survived or were invalidated. The knowledge ledger alone can say how much within-episode discovery, retained knowledge gain, or knowledge loss was recorded for a closure-indexed row. Only the joined ledger can ask whether different operational classes of closures have different epistemic profiles.

For example, in the goal-model-revision ledger, the provisionally accepted closure history is:

{\hat{C}}_{I}^{+} := (c_{u} : t_{a} < u \leq t_{b}, z_{u} \in {\hat{O}}_{u}) .

The authoritative surviving subset is:

C_{I, net} := (c_{u} \in {\hat{C}}_{I}^{+} : z_{u} \in O^{*}) .

The model-invalidated subset is:

C_{I, model-loss} := (c_{u} \in {\hat{C}}_{I}^{+} : z_{u} \notin O^{*}) .

These two subsets partition the provisional closure history:

S_{gross}^{\hat{}} (I) = S_{net} (I) + W_{model} (I) .

Now join these operational subsets with the knowledge-ledger rows on the shared closure-event index. For closures that survived authoritative checking, the average within-episode discovery is:

B_{avg}^{disc,net} (I) := \frac{1}{S_{net} (I)} \cdot \sum_{c_{u} \in C_{I, net}} B_{u}^{disc} .

Average within-episode KTD reduction for net surviving closures equals the average amount by which those episodes reduced residual Knowledge To Be Discovered between episode start and episode termination.

${ΔKTD}_{avg}^{within,net} (I) := \frac{1}{S_{net} (I)} \cdot \sum_{c_{u} \in C_{I, net}} (H_{u}^{start} - H_{u}^{term}) .$

This is equivalent to the B version, because:

B_{u}^{disc} = H_{u}^{start} - H_{u}^{term} .

We can compute the ex-ante expected conditional entropy over all possible observation states:

${KTD}_{avg}^{start,net} (I) := \frac{1}{S_{net} (I)} \cdot \sum_{c_{u} \in C_{I, net}} H_{u}^{start} .$

(1)

It answers: before observing which knowledge state actually occurred, what is the expected uncertainty about the required response class, averaged over possible values of $Y$ ?

We can also compute how much ignorance remained after within-episode discovery:

{KTD}_{avg}^{term,net} (I) := \frac{1}{S_{net} (I)} \cdot \sum_{c_{u} \in C_{I, net}} H_{u}^{term} .

Then how much ignorance was removed inside those episodes:

${ΔKTD}_{avg}^{within,net} (I) = {KTD}_{avg}^{start,net} (I) - {KTD}_{avg}^{term,net} (I) .$

For closures that were invalidated by goal-model revision, the corresponding average within-episode discovery is:

B_{avg}^{disc,model-loss} (I) := \frac{1}{W_{model} (I)} \cdot \sum_{c_{u} \in C_{I, model-loss}} B_{u}^{disc} .

These two quantities can be compared. They answer the joined-ledger question: do surviving closures and invalidated closures differ in the amount of within-episode discovery they required or produced? This question is invisible to either ledger alone.

The same join can be used for other epistemic quantities. For example, one may compare retained knowledge gain:

G_{avg}^{K, net} (I) := \frac{1}{S_{net} (I)} \cdot \sum_{c_{u} \in C_{I, net}} G_{u}^{K}

with retained knowledge gain for model-invalidated closures:

G_{avg}^{K, model-loss} (I) := \frac{1}{W_{model} (I)} \cdot \sum_{c_{u} \in C_{I, model-loss}} G_{u}^{K} .

The same convention applies to all conditional averages: if the denominator is zero, the corresponding average is undefined for that window.

The ledgers can be joined, conditioned, compared, and reported together. What should be avoided is treating closure counts and KTD bits as if they belonged to one conservation equation. The operational identity partitions closure counts. The knowledge-ledger identity tracks bit-valued changes in residual Knowledge To Be Discovered. The joined measures condition bit-valued quantities on operational event classes. They are valid measurement queries, but they do not collapse the operational and knowledge ledgers into one common unit.

Average KTD is not pooled entropy

The window statistic ${KTD}_{avg}^{τ_{j}} (I)$ is not the entropy of a single pooled task variable. In general:

{KTD}_{avg}^{τ_{j}} (I) \neq H (X_{I} | Y_{I})

The left-hand side averages the conditional entropies attached to individual closure-indexed rows. The right-hand side would require constructing a new pooled probability model over window-level variables. Those are different operations.

For the same reason, the exact per-row duality between change in stored coupling and change in residual KTD does not automatically become an aggregate identity for window averages. In general:

Δ {KTD}_{avg}^{τ_{j}} (I) \neq - Δ I_{avg}^{τ_{j}} (I)

Such a dual reading is valid only under stronger comparability conditions: the same task-class frame, the same response-equivalence abstraction, the same modeling resolution, and a fixed marginal entropy of the required response-equivalence variable. Even then, the identity applies cleanly at the row or matched-row level. Sliding-window averages add sampling, weighting, and window-composition effects.

Sliding-window series

Moving the window over time produces a measurement series. For a sequence of window endpoints $s_{0} < s_{1} < s_{2} < \dots$ , define:

I_{m} := (s_{m - 1}, s_{m}] .

Then the task-class-specific KTD trend is the sequence:

{KTD}_{avg}^{τ_{j}} (I_{1}), {KTD}_{avg}^{τ_{j}} (I_{2}), {KTD}_{avg}^{τ_{j}} (I_{3}), \dots

A downward trend means that comparable episodes are beginning with less residual Knowledge To Be Discovered on average. An upward trend means that comparable episodes are beginning with more residual Knowledge To Be Discovered on average. A flat trend means that the regulator's stored coupling is not measurably changing at the chosen task-class granularity, or that gains and losses are offsetting within the window.

Summary

Window-level accounting turns the closure-indexed ledgers into practical measurement series. The operational ledger supplies counts of produced, surviving, and invalidated closures. The knowledge ledger supplies bit-valued measures of residual ignorance, within-episode discovery, retained gain, and knowledge loss.

The key practical statistic is:

{KTD}_{avg}^{τ_{j}} (I)

is average starting residual ignorance over comparable ledger rows in the window.

It is a useful summary statistic, not a replacement for the per-row knowledge-ledger identity. It should be read as an average burden of discovery carried into episodes, not as the entropy of a single pooled variable and not as the direct knowledge analogue of $S_{gross} = S_{surv} + W$ . The knowledge analogue remains the per-task-class stock-flow identity:

H_{u + 1}^{start} = H_{u}^{start} - G_{u}^{K} + L_{u}^{K},

applied row by row and then summarized over the window.

Feedback-loop reading of revisions and the operational ledger

The preceding sections distinguish closure, acceptability, behavioral revision, learning, goal revision, goal-model revision, and ledger accounting. These constructions can now be read uniformly as feedback-loop-induced changes. The key point is that feedback does not name one kind of change. It names a loop in which a produced outcome is evaluated and the resulting signal is returned to some part of the regulatory system. What kind of revision occurs depends on what the feedback signal changes.

In the present formulation, the operational ledger is not itself the feedback loop. It is the memory trace that makes feedback across episodes observable. The feedback loop is the process by which closure events are recorded, evaluated, and then used to revise a response rule, a goal criterion, a believed goal model, or the regulator's stored law of action.

This is the cybernetic reading of regulation as a system of nested loops, where each loop is identified by its error signal, its revision target, and its characteristic time scale[7][57]. Ashby's two-loop scheme for adaptive machines is the historical antecedent: a fast inner loop selects responses within a fixed structure, and a slow outer loop changes the structure when essential variables leave the acceptable region[1][7].

The present formulation distinguishes three loops, because the formal model separates within-episode selection, across-episode learning of the response coupling, and revision of the goal or the regulator's model of the goal.

Feedback as a loop, not a revision type

At the first order, the regulator selects a response for a disturbance. A disturbance-value $d$ is paired with a response-value $r$ , and the Table of Outcomes produces the closure outcome:

z = T (d, r) .

The closure is then evaluated through the outcome-to-essential-variable map and the acceptable region prevailing at that time:

φ (z) \in η_{t} or φ (z) \notin η_{t} .

A feedback signal is generated when this evaluation is returned to the regulator. But the feedback signal becomes a revision only when it changes some component of the regulatory system. If it changes the active response rule, the result is behavioral revision. If it changes the stored law of action, the result is learning. If it changes the acceptable region, the result is criterion revision. If it changes the regulator's believed model of the acceptable region, the result is goal-model revision.

Thus invalidation is not itself learning, and it is not itself corrective rework. Invalidation is a feedback signal. Learning, behavioral revision, criterion revision, and model revision are different possible uses of that signal.

The regulatory state

Throughout this section, the fixed environmental frame is still the Table of Outcomes:

T : D \times R \to Z

with outcome-to-essential-variable map:

φ : Z \to E .

In the fixed-table case, these remain fixed. The revisable regulatory state at episode index $t$ can be written as:

Θ_{t} := (M_{t}, ρ_{t}, {\hat{η}}_{t}, η_{t}) .

Here $M_{t}$ is the stored law of action, $ρ_{t}$ is the active response rule, ${\hat{η}}_{t}$ is the regulator's believed acceptable essential-variable region, and $η_{t}$ is the authoritative acceptable region prevailing at time $t$ .

The acceptable outcome-set induced by the authoritative region is:

O_{acc, t} := φ^{- 1} [η_{t}] .

When the regulator acts under an imperfect model of the goal, its believed acceptable outcome-set is:

{\hat{O}}_{t} := φ^{- 1} [{\hat{η}}_{t}] .

The three loops

Each loop is identified by its error signal, by the component of the regulatory state it revises, and by the time scale on which it operates. All three loops are negative-feedback loops in the cybernetic sense: each acts to reduce a measured discrepancy between an observed quantity and a reference[7].

Loop L1 — selection within an episode

L1 is the inner regulatory loop. Its reference is the acceptable outcome-set $O_{acc, t}$ , or its believed counterpart ${\hat{O}}_{t}$ when the regulator acts under an imperfect model.

Its error signals are the within-episode selection signals $U_{i}$ generated by action units $q_{i}$ . Its output is the staged narrowing of the candidate response-set:

\emptyset \neq C_{k} (d) \subseteq \dots \subseteq C_{1} (d) \subseteq C_{0} (d) \subseteq R .

The loop terminates when the regulator commits a response $r_{t}$ and produces the closure:

z_{t} = T (d_{t}, r_{t}) .

L1 operates within one episode. It does not, by itself, alter the stored law of action, the believed goal model, or the authoritative acceptable region. This is Ashby's first feedback loop, the error-controlled regulator[1][7].

Loop L2 — learning across episodes

L2 is an outer loop whose reference is reduction in residual Knowledge To Be Discovered for a comparable task class. Its error signal includes the closure-valuation:

v_{t} := 1_{{φ (Z_{t}) \in η_{t}}},

together with the within-episode evidence stream $U_{t}$ , the response class actually fixed, the final concrete response, and the produced closure. Its output is the update:

M_{t} \to M_{t + 1} .

When successful by the learning axiom, L2 reduces the residual lack of requisite knowledge at the start of the next comparable episode:

H_{t + 1} (X | Y) < H_{t} (X | Y) .

L2 operates across episodes within a window of comparable task instances. It corresponds to adaptive learning of a pattern of behavior appropriate for the environment[1][7].

Loop L3 — revision of the goal or the goal model

L3 is a higher-order outer loop whose reference is alignment of the criterion of success used by the regulator with the criterion against which closures are ultimately judged. It has two forms, corresponding to the two ledger cases developed above.

In the external goal-revision form, the trigger is an exogenous change in the authoritative acceptable region:

η_{t_{1}} \to η_{t_{2}} .

This change propagates into the acceptable outcome-set through the pullback along $φ$ , yielding deletion, addition, and substitution operations on $O_{acc, t}$ .

In the goal-model-revision form, the authoritative region remains fixed. The feedback signal is checking evidence that registers a mismatch between the regulator's believed acceptable set and the authoritative set:

{\hat{O}}_{v^{-}} \neq O^{*} .

The output is a model-revision event that revises the believed acceptable region:

{\hat{η}}_{v^{-}} \to {\hat{η}}_{v} .

In both forms, L3 does not by itself produce behavior. It revises the criterion against which behavior is judged. Behavioral consequences arise only when L1 is re-engaged under the revised criterion, possibly using a different response rule.

Mapping revision targets to feedback loops

All revision types can be represented as feedback-induced changes, provided the loop level and revision target are made explicit. The type of feedback-induced revision is determined by which component of the regulatory state is changed.

Construction or revision type	Loop	Feedback signal / trigger	Revision target	Cybernetic interpretation
Staged selection trace	L1	Selection signals $U_{i}$	Candidate response-set $C_{i} (d)$	The regulator narrows possible responses within one episode.
Closure	L1 terminal output	Commitment of $r_{t}$	Realized outcome-value $z_{t}$	The episode closes when a committed response produces an outcome.
Behavioral revision	L1 re-engaged	Prior closure evaluation or invalidation	Response rule $ρ_{t} \to ρ_{t + 1}$	Feedback changes what response rule the regulator uses.
Learning	L2	Closure-valuation, evidence stream, and retained episode information	Stored law of action $M_{t} \to M_{t + 1}$	Feedback changes the stored coupling used in later comparable episodes.
Learning success criterion	L2	Across-episode reduction of conditional entropy	Residual Knowledge To Be Discovered	The next comparable episode starts with less response-class uncertainty.
Criterion revision	L3 external goal-revision form	Exogenous change in the authoritative acceptable region	$η_{t} \to η_{t + 1}$	Feedback or external change revises the criterion of success.
Acceptability deletion, addition, and weak substitution	L3 external goal-revision form	Change in $η_{t}$	Pullback acceptable outcome-set $O_{acc, t}$	Fixed outcome-values gain or lose acceptability; they are not deleted from $T$ .
Strict substitution	L3 external goal-revision form	Criterion revision plus replacement pairing supplied by the model	Replacement correspondence $λ_{12}$	The model specifies which lost acceptable value is replaced by which gained value.
Goal-model revision	L3 goal-model form	Checking evidence against the authoritative acceptable set	Believed acceptable region ${\hat{η}}_{t} \to {\hat{η}}_{t + 1}$	Feedback changes the regulator's model of the goal, not the authoritative goal itself.
Model-revision event	L3 goal-model form	Authoritative checking or mismatch evidence	Model revision event $m_{v}$	The believed loss and gain sets are induced by revising the goal model.
Corrective replacement	L1 re-engaged after L3	Invalidation of an earlier closure	Repair relation $κ (c_{u}, c_{v})$	A later closure is treated as repairing an earlier invalidated closure.
Structural adaptation	Higher-order adaptation beyond the fixed-table case	Persistent failure or insufficiency of the existing regulatory frame	$T, D, R, Z, E, φ may change$	Feedback changes the system structure or the available regulatory repertoire.

The present fixed-table formulation allows behavioral revision, criterion revision, goal-model revision, and learning while holding $T$ , $D$ , $R$ , $Z$ , $E$ , and $φ$ fixed. Structural adaptation is a stronger case and should be modeled separately.

The operational ledger as feedback memory

The operational ledger records the closure history produced by L1. It preserves closure events after their production, allowing the system to evaluate not only whether a closure was acceptable when produced, but also whether it continues to survive later criteria, later model revisions, or later authoritative checking.

Let the operational ledger up to time $t$ be the time-ordered history of recorded closure events:

L_{t} := (c_{u} : u \leq t), c_{u} = (u, d_{u}, r_{u}, z_{u}) .

The ledger answers the accounting question: which closures were produced, which survived, and which were invalidated? The feedback-loop formulation answers the question: which part of the regulator changed because closure evaluations were fed back into the system?

A feedback signal is generated when the ledger is evaluated against some current or authoritative criterion. In the external criterion-revision case, a prior closure may be invalidated because:

z_{u} \in O_{acc, u} but z_{u} \notin O_{acc, t}, u < t .

In the goal-model-revision case, a prior provisional closure may be invalidated because:

z_{u} \in {\hat{O}}_{u} but z_{u} \notin O^{*} .

These facts are ledger-visible feedback signals. They become revisions only when they are used to change some component of the regulatory state. Thus the ledger supplies feedback memory, but it does not collapse invalidation, learning, and repair into the same event.

The operational ledger as cross-loop bookkeeping

Under this reading, the operational ledger is bookkeeping over L1's closure history after L2 and L3 events inside the window have had their effects. Each ledger quantity has a loop interpretation.

The gross counted closures $S_{gross} (I)$ and the gross provisional closures $S_{gross}^{\hat{}} (I)$ count L1 outputs admitted under the criterion or believed criterion prevailing at production time. They are work-counts of closure-fixing acts.

The invalidation load $W (I)$ counts L1 closures that L3, in its external goal-revision form, later invalidated by changing $η_{t}$ somewhere in the window.

The goal-model invalidation load $W_{model} (I)$ counts L1 closures that L3 (goal-model form) later invalidated by revising ${\hat{η}}_{t}$ against the fixed authoritative $η^{*}$ . Both are L3-attributable invalidations of prior L1 work.

The surviving counted closures $S_{surv} (I)$ and the net surviving closures $S_{net} (I)$ count L1 closures that were not invalidated by the relevant L3 process within the window.

The two ledger identities therefore have direct loop readings:

S_{gross} (I) = S_{surv} (I) + W (I)

S_{gross}^{\hat{}} (I) = S_{net} (I) + W_{model} (I)

The first says that total accepted L1 output equals L1 output that continuously survived plus L1 output later invalidated by criterion revision. The second says that total provisional L1 output equals authoritatively surviving L1 output plus L1 output invalidated by goal-model mismatch.

Neither identity is an entropy identity. Both are operational accounting identities. They count closure-fixing acts, not bits of Knowledge To Be Discovered.

The ledger therefore answers a question that none of the three loops answer in isolation: over a window, how much of L1's produced closure history was preserved, and how much was retroactively invalidated by later criterion or model evaluation?

Invalidation, repair, and corrective rework

The ledger can show that a closure was invalidated, but invalidation is not the same as corrective rework. Invalidation is a feedback signal. Corrective rework requires a later behavioral event that repairs, replaces, or compensates for the invalidated closure.

Thus a feedback-induced corrective replacement requires additional structure beyond the invalidation count. If $c_{u}$ is an invalidated closure and $c_{v}$ is a later closure, introduce a repair relation:

κ (c_{u}, c_{v}) .

This means that the later closure event $c_{v}$ is treated as the corrective replacement for the earlier invalidated closure $c_{u}$ . The relation $κ$ is not determined by the ledger alone. It is additional modeling structure that identifies which later closure repairs which earlier invalidation.

At minimum, a repair relation should satisfy: $κ (c_{u}, c_{v}) \Rightarrow u < v$ and $c_{u}$ is invalidated and $c_{v}$ is accepted under the relevant criterion.

For a goal-model-revision ledger with fixed authoritative acceptable set, this can be written more specifically as:

$κ (c_{u}, c_{v}) \Rightarrow u < v and z_{u} \notin O^{*} and z_{v} \in O^{*} .$

In the typing example, a natural repair relation may also require that both closure events address the same target position:

κ (c_{u}, c_{v}) \Rightarrow p_{u} = p_{v} .

The full feedback sequence is therefore:

closure → ledger record → evaluation → feedback signal → revision → possible corrective closure.

This is the cybernetic role of the operational ledger: it makes closure history available for later feedback, but it does not collapse invalidation, learning, and repair into the same event.

Time-scale separation and loop interaction

The three loops are separated by characteristic time scales, in the cybernetic tradition of nested adaptive control[1][7][57]. L1 operates within a single episode and terminates with a closure. L2 operates across consecutive comparable episodes within a window. L3 operates on an episodic-to-rare time scale, depending on whether the trigger is an exogenous goal change or a discovered model mismatch.

Because L3 acts outside the immediate L1 closure event, an L3 event inside a window can retroactively rewrite the acceptability-status of L1 closures already produced. This is why the operational ledger must track not only gross production count but also survival count under the criterion history or authoritative checking structure of the window.

Because L2 acts between L1 episodes, an L2 update changes the prior structure of the next L1 episode. It does not, by itself, change the status of past closures. Therefore $W (I)$ and $W_{model} (I)$ are L3-attributable invalidation loads, not L2 learning measures.

Loop interaction is still possible. An L3 invalidation may become an error signal for L2: a closure that ceased to count under a revised criterion provides evidence that the stored coupling $M_{t}$ was aligned with the old criterion or the old believed model, not with the revised one.

Conversely, repeated L2 success may reduce the need for L3 in the goal-model-revision case by bringing the regulator's believed model into alignment with the authoritative criterion. This cross-loop coupling matches Ashby's observation that the adaptive loops of an ultrastable machine interact, with the slow loop reorganizing the structure on which the fast loop operates[1][7].

The present formulation models these loops as negative-feedback loops on their respective error signals. Positive-feedback dynamics — such as exploratory expansion of the candidate set, variety-amplifying changes to the stored law of action, or deliberate broadening of the believed acceptable region — would require explicit additional structure and are not part of the fixed-table formulation developed here.

Summary

Read as a feedback-loop system, the formal model has three loops. L1 selects responses within an episode and closes it. L2 updates the stored law of action across comparable episodes and is evaluated by the learning axiom. L3 revises the criterion of success, either exogenously through external goal revision or endogenously through goal-model mismatch discovery.

The operational ledger is the cross-loop bookkeeping that records how L1's closure history was preserved or invalidated within an observation window. It is not itself the feedback loop. It is the memory trace that allows later evaluation, feedback, revision, and possible repair.

This reading does not introduce new formal objects. It names the cybernetic role of each construction already defined above and exhibits the regulatory model as a nested loop hierarchy in the sense of Ashby's adaptive machine and its successors[1][7][57].

Quantifying the Knowledge Discovery Process

How is the desired regulator to be brought into being? With whatever variety the components were initially available, and with whatever variety the designs might have varied from the final appropriate form, the maker acted in relation to the goal so as to achieve it. He therefore acted as a regulator. Thus the making of a machine of desired properties is itself an act of regulation.

From latent ignorance to operational measurement

The preceding sections defined the Knowledge Discovery Process in two related ways. Inside a regulatory episode, it is the staged reduction of Knowledge To Be Discovered. Across comparable episodes, it is the retained reduction of Knowledge To Be Discovered in the regulator's stored law of action. Those definitions are information-theoretic. They refer to quantities such as $H (X | Y)$ , where $X$ is the required response-equivalence class and $Y$ is the disturbance information available to the regulator.

In practice, however, we usually do not observe the regulator's full internal probability model, its true posterior distribution over response-equivalence classes, or every internal staged selection. What we observe is the external execution trace: closure events, surviving closures, invalidated closures, and in some cases counted action units consumed by the shared execution channel.

The purpose of this section is therefore not to claim direct observation of $H (X | Y)$ . The purpose is to define an operational estimator that uses the ledgers already introduced: the operational ledger supplies closure counts and invalidation counts, while the knowledge ledger supplies the bit-valued latent quantities against which the estimator is interpreted.

The goal of this section is to construct an operational estimator related to ${KTD}_{avg}^{start-real,net} (I)$ from those observables, and to derive, as a direct corollary, the increase in effective question depth attributable to observable invalidation load.

The key distinction is this: the latent quantity is average realized starting Knowledge To Be Discovered; the operational estimator is average effective question depth under the one-bit action-unit coding convention. The two are related, but they are not the same object.

The structure of the construction is two-layered. The latent estimand is the realized knowledge-ledger quantity defined in equation (2). The operational estimator built below is its aggregate-channel counterpart, expressed in terms of the operational ledger quantities $(N, S_{gross}, W, S_{net})$ only. The two layers are bridged by the ideality assumptions (A1)–(A5) collected below, of which the most important asserts that each counted non-closure atomic action unit contributes one bit of response-relevant binary discrimination.

Thus, this section separates three quantities that must not be collapsed.

Latent Knowledge To Be Discovered: the average realized starting posterior entropy of knowledge-ledger rows whose closures survive as accepted.
Operational one-bit estimator: the observed average effective one-bit action-unit depth per net surviving closure.
Invalidation-induced increase in effective question depth: the difference between the net one-bit estimator and the fixed-gross no-invalidation baseline.

Latent window-level estimand

For the operational ledger, the relevant latent quantity is the realized row-level Knowledge To Be Discovered $H_{M_{u}} (X ∣ Y = y_{u})$ , evaluated at the disturbance information actually observed for closure $u$ , and not the ex-ante conditional entropy $H_{M_{u}} (X ∣ Y)$ averaged over all possible observation states.

The knowledge ledger's $H_{u}^{start} := H_{M_{u}} (X ∣ Y)$ is the expected stored-coupling quantity used in the learning and stock-flow identities. The quantity needed here is its realized counterpart at the observed $Y = y_{u}$ :

H_{u}^{start,real} := H_{M_{u}} (X ∣ Y = y_{u}) .

Here $X$ is the required response-equivalence class and $Y = y_{u}$ is the realized disturbance information available to the regulator at the start of episode $u$ .

The two quantities are linked. For a fixed knowledge state $M_{u}$ , the expected conditional entropy is the $Y$ -average of the realized posterior entropies:

H_{M_{u}} (X ∣ Y) = \sum_{y} P_{M_{u}} (Y = y) H_{M_{u}} (X ∣ Y = y) .

Consequently, when the knowledge state is stable across the window and the realized observations $y_{u}$ among the net surviving closure population are representative of the relevant $M$ -induced marginal distribution on $Y$ , the row average of $H_{u}^{start,real}$ is an unbiased estimator of the common expected quantity $H_{M} (X ∣ Y)$ . Where the knowledge state drifts or the realized disturbance mix is atypical, the two diverge, and the realized average — not the expected one — is what the operational construction below targets.

The operational ledger determines which closure events survive as accepted closures in the window. Let the net surviving closure history be:

C_{I, net} := (c_{u} : c_{u} survives as accepted in I) .

The corresponding net surviving closure count is:

S_{net} (I) := | C_{I, net} | .

In this section, $S_{net} (I)$ denotes the surviving accepted closure count under whichever ledger is being used. In the external criterion-revision ledger, $S_{net} (I)$ corresponds to $S_{surv} (I)$ . In the goal-model-revision ledger, it corresponds to the authoritative net surviving count already denoted $S_{net} (I)$ .

The knowledge ledger attaches a knowledge row $k_{u}$ to each closure event $c_{u}$ . Define the knowledge-ledger rows joined to the net surviving closure history:

K_{I, net} := (k_{u} : c_{u} \in C_{I, net}) .

The latent realized average starting Knowledge To Be Discovered for surviving closures is therefore:

${KTD}_{avg}^{start-real,net} (I) := \frac{1}{S_{net} (I)} \cdot \sum_{k_{u} \in K_{I, net}} H_{u}^{start,real} .$

(2)

This is the latent estimand for the operational construction. It is an average conditioned on the operational event class “surviving accepted closures.” It is not the entropy of a pooled window-level variable, and it is not yet an operational count.

It is the realized counterpart of equation (1), which averages the expected starting Knowledge To Be Discovered $H_{M_{u}} (X ∣ Y)$ over all possible observation states for the window, whereas equation (2) averages the realized posterior ignorance $H_{M_{u}} (X ∣ Y = y_{u})$ over the same surviving closures. The two coincide only under the stationarity and representativeness condition stated with equation (2); in general the operational construction below targets the realized average ${KTD}_{avg}^{start-real,net} (I)$ , not the expected average ${KTD}_{avg}^{start,net} (I)$ of equation (1).

This realized estimand is latent: under black-box observation we do not see the internal stages of an episode, we do not see the regulator's knowledge state $M_{u}$ , and we do not see the per-stage selection signals $U_{i}$ . What we do see is the externally visible execution channel — closure events and the atomic action units between them — together with the operational ledger that records which gross closures survived as net accepted closures inside the window.

Ideal binary-question-depth layer

The remaining uncertainty in a closure is latent: it concerns the response-equivalence class that would have to be selected for the realized disturbance, but that class is not directly observed as a visible work item, question, or decision step. To make this latent uncertainty operational, we need a bridge from entropy to ideal inquiry effort.

Lemma 1 — One-bit coding bracket. For each realized episode u, let the posterior distribution over required response-equivalence classes after the realized disturbance information is observed be:

P_{u, y_{u}} (x) := P_{M_{u}} (X = x ∣ Y = y_{u}) .

Let $q_{u}^{⋆} (y_{u})$ denote the minimum expected number of binary yes/no questions required to identify X under this posterior distribution. Equivalently, $q_{u}^{⋆} (y_{u})$ is the expected depth of an optimal binary decision tree for $P_{u, y_{u}}$ . Assume the posterior support of X under $Y = y_{u}$ is finite, or countable with finite entropy, so that the standard binary source-coding bracket applies.

In this lemma, a question means one binary distinction, ideally a yes/no distinction, used to reduce uncertainty about the required response-equivalence class. Question depth is the number of such binary distinctions needed along a particular inquiry path. Expected question depth is the average number of binary distinctions required under a probability distribution over possible response classes. Thus, question depth is literally the number of questions only in the ideal binary-question model

Then the optimal expected binary-question depth is bracketed by the posterior entropy within one bit:

$H_{M_{u}} (X ∣ Y = y_{u}) \leq q_{u}^{⋆} (y_{u}) < H_{M_{u}} (X ∣ Y = y_{u}) + 1.$

Here, the per-row posterior entropy $H_{M_{u}} (X ∣ Y = y_{u})$ is exactly $H_{u}^{start,real}$ evaluated at the realized $y_{u}$ .

In the special case where the posterior distribution is uniform over 2^m equiprobable response classes, the bracket is tight: $H_{M_{u}} (X ∣ Y = y_{u}) = m .$ . For example, if a coin is hidden in one of eight equally likely boxes, then $(H (X) = \log_{2} 8 = 3)$ , and the optimal binary-question strategy identifies the box in exactly three questions.

Averaged over the net surviving closure population $C_{I, net}$ in window I , the corresponding ideal-depth benchmark is:

${KTD}_{avg}^{start-real,net} (I) \leq {\bar{E}}_{I, net}^{} [q^{⋆}] < {KTD}_{avg}^{start-real,net} (I) + 1$

(3)

where ${\bar{E}}_{I, net}^{} [q^{⋆}]$ denotes the average ideal binary question depth over net surviving closures in window I.

Equation (3) is the latent-to-ideal bridge. It says that the average optimal binary-question depth over net surviving closures brackets the latent ${KTD}_{avg}^{start-real,net} (I)$ realized average Knowledge To Be Discovered within the standard sub-one-bit source-coding gap. It is purely information-theoretic. It does not yet involve any observable execution counts, and it does not yet say that the observed execution trace followed an optimal binary-questioning procedure. That stronger reading enters only through the ideality assumptions stated below.

Proof. The result follows from the standard source-coding interpretation of entropy: an optimal binary decision or coding procedure has expected length at least the entropy and less than entropy plus one bit. Averaging this per-row bracket over the net surviving closure population preserves the inequalities.

The bridge says that the posterior entropy $H_{M_{u}} (X ∣ Y = y_{u})$ is not merely an abstract measure of missing knowledge; it is the idealized binary-question complexity of identifying the required response-equivalence class, up to the standard one-bit gap. Lemma 1 establishes this connection, allowing ${KTD}_{avg}^{start-real,net} (I)$ to be interpreted as the average amount of knowledge that still had to be discovered per net surviving closure.

Operational assumptions

The operational construction uses a fixed observation window:

I = (t_{a}, t_{b}] .

The following assumptions define the operational measurement model. They are not epistemological claims about how the regulator thinks. They are coding assumptions about how the externally visible execution trace is counted.

Assumption A1 — Fixed counted channel capacity. The observation window $I$ has a fixed counted action capacity $N (I)$ . This is the total number of counted atomic action units available or consumed in the window.

Assumption A2 — Exhaustive unit classification. Every counted atomic action unit is classified as exactly one of two types: a non-closure discrimination unit or a closure unit. No counted unit belongs to both classes.

Assumption A3 — Net survival. The net surviving closure count equals the number of gross closures that remain accepted under the relevant window-level evaluation rule. Gross closures that fail to survive consumed capacity but do not contribute to net accepted closure output.

Assumption A4 — Closure counting. Each gross closure event consumes one closure unit when produced. A gross closure may later survive as accepted or be invalidated by the relevant evaluation criterion.

Under A1-A4, the operational identities below are exact. They do not require access to the regulator's internal knowledge state $M_{t}$ , to posterior probabilities, or to the internal order of staged selections inside an episode.

Operational action-unit layer

The ideal binary-question-depth layer concerns the minimum expected number of binary distinctions required under an ideal questioning scheme. The operational layer concerns what was actually counted in the execution channel. Under A1-A4, the execution stream is partitioned into counted non-closure discrimination units and gross closure units.

Let $N (I)$ denote the fixed counted action capacity of window $I$ . This capacity includes both non-closure discrimination units and gross closure units.

Let $S_{gross} (I)$ be the number of gross closure units in that window.

Proposition 1 — Channel partition identity. Under A1–A2, the channel capacity $N (I)$ is exhaustively partitioned into non-closure action units and gross closure units. Writing $Q (I)$ for the number of non-closure action units $q_{i}$ physically present in the window, and $S_{gross} (I)$ for the number of gross closure units,

Q (I) = N (I) - S_{gross} (I) .

This is a pure accounting identity: on a single fixed-capacity channel, every counted unit is either a non-closure action unit $q_{i}$ or a gross closure unit, and $Q (I)$ counts the former by tallying action units, with no recoding.

Proof. By A2, every counted unit is either a non-closure discrimination unit or a closure unit. By A4, gross closures are the closure units. Therefore the non-closure count equals total counted capacity minus gross closure count.

The black-box constraint matters here: under this observation model we can attribute each atomic unit to either the closure stream or the non-closure stream, but we cannot see the internal staged structure inside an episode. The execution channel makes $Q$ and $S_{gross}$ observable; the operational ledger then makes $W$ and $S_{net}$ observable as well.

Observable invalidation load and net surviving closures

For the quantification below, the relevant observable invalidation load $W_{obs} (I)$ is the gross closures in window I that fail to survive as net accepted closures.

By A3:

S_{net} (I) = S_{gross} (I) - W_{obs} (I) .

This identity is operational, not entropic. It partitions gross closure work into net surviving closure work and observable invalidation load.

The counted channel capacity $N (I)$ is held fixed throughout. Under A1–A2 and A4, the physical unit count of the channel admits exactly one physical partition into atomic action units, namely Proposition 1:

N (I) = Q (I) + S_{gross} (I) (physical partition) .

In this partition each of the $W_{obs} (I)$ invalidated closures is counted once, as a consumed gross-closure unit inside $S_{gross} (I)$ . The invalidated closures are real units; they occupy capacity on the channel.

The effective non-net-progress load in window $I$ is:

Q_{eff} (I) := Q (I) + W_{obs} (I) .

$Q_{eff} (I)$ is not a count of channel units. It is the physical non-closure count $Q (I)$ augmented by a one-unit non-progress debit for each invalidated gross closure. By construction $Q_{eff} (I) \geq Q (I)$ , with equality if and only if $W_{obs} (I) = 0$ ; whenever invalidation occurs, $Q_{eff} (I)$ strictly exceeds the number of non-closure units actually present on the channel.

Combining the definition with $S_{net} = S_{gross} - W_{obs}$ :

Q_{eff} (I) + S_{net} (I) = (Q + W_{obs}) + (S_{gross} - W_{obs}) = Q + S_{gross} = N (I) .

So the same fixed capacity $N (I)$ admits a second, effective partition:

N (I) = Q_{eff} (I) + S_{net} (I) (effective progress partition) .

The two partitions of $N (I)$ differ only in the bookkeeping of the invalidated closures, and $N (I)$ itself is unchanged.

Operational one-bit effective-depth estimator.

Proposition 1 and the channel partition identities require only the pure accounting assumptions. The interpretation of the resulting ratios as one-bit question-depth measures additionally requires A5. The interpretation of the resulting ratios as latent information-theoretic KTD additionally requires Lemma 1 and B1–B4 later on.

Assumption A5 — Operational one-bit reading. The count $Q (I)$ of non-closure action units is fixed by Proposition 1 and is not recoded. A5 is the convention by which that fixed count is read as a binary-question depth: each counted action unit $q_{i}$ is taken to be one binary narrowing step on the live concrete candidate set $C_{i}^{R} (d)$ — one probe that partitions the live candidates and discards one side, in the manner of one step of dichotomy search. The count-variety value of a single even split is one bit:

\log_{2} (| C_{i - 1}^{R} (d) | / | C_{i}^{R} (d) |) = 1 .

Because the count is held fixed at the number of action units, A5 does not re-count uneven or $m$ -way splits as several units, and does not drop action units that happen to narrow the live set not at all (the epistemically-null case). Instead, the discrepancy between the one-step charge assigned to each $q_{i}$ and its true binary-question content is carried, in aggregate, into the calibration error $ϵ_{c a l} (I)$ introduced in B1. Consequently the depth ratios ${\hat{KTD}}_{base}^{1bit} (I)$ and ${\hat{KTD}}_{eff}^{1bit,net} (I)$ are action-units-per-closure, computed from the fixed count $Q (I)$ .

A5 is therefore a purely combinatorial reading convention on the action-unit count. It is the one-bit-per-even-split special case of the per-stage count-variety selection $σ_{i}^{set}$ already defined for the staged trace, anchored to the concrete candidate set $C_{i}^{R} (d)$ that the operational ledger records. It invokes neither a probability model over the required response-equivalence class $X$ nor entropy; the reading of these counted steps as questions about $X$ is deferred to B1, and the only genuine assumption (not a definition) is that scoring each action unit as one even split is exact only for even splits, with all deviation absorbed by $ϵ_{c a l}$ .

Two things to note. First, A5 is anchored to $C_{i}^{R} (d)$ — the concrete candidate response-set from the set-based trace — so the probes are operationally visible narrowings of actual responses, which is what the operational ledger records. Second, the "one bit per even split" clause is the genuine assumption (not a definition): scoring every probe as one unit is exact only for even splits. That is the thing B1 then has to calibrate.

Definition (Fixed-gross no-invalidation baseline). The baseline is a contrast operator on observables, not a causal counterfactual. Hold fixed the observed channel capacity $N (I)$ and the observed gross closure count $S_{gross} (I)$ fixed, and set the observable invalidation load to zero, $W_{obs} (I) := 0$ , so that $S_{net} (I) = S_{gross} (I)$ . The baseline question depth per closure is then the average number of non-closure atomic units per gross closure:

${\hat{KTD}}_{base}^{1bit} (I) := \frac{Q (I)}{S_{gross} (I)} = \frac{N (I) - S_{gross} (I)}{S_{gross} (I)} - 1 := \frac{N (I)}{S_{gross} (I)} - 1 .$

(4)

The baseline reads the physical partition of the channel, which counts the invalidated closures as closures. Because it is defined by fixing observables and zeroing the invalidation load, equation (4) is exact as an operational count by construction. It is not a counterfactual estimate of what would have happened absent invalidation; it is the value of the same operational ratio evaluated at $W_{obs} = 0$ . This removes any need to defend the baseline as a causal alternative, and it supplies the fixed-gross reference against which the effect of observable invalidation load is measured below.

The effective question depth means the estimated average number of one-bit-equivalent action units per surviving closure. The operational one-bit estimator for average effective question depth per net surviving closure is:

${\hat{KTD}}_{eff}^{1bit,net} (I) := \frac{Q_{eff} (I)}{S_{net} (I)} = \frac{N (I) - S_{net} (I)}{S_{net} (I)} = \frac{N (I)}{S_{net} (I)} - 1 .$

(5)

The net estimator reads the effective partition of the channel, which counts the invalidated closures as load. By construction, it is also exact as an operational count. Equation (5) is exact as an operational estimator of average effective one-bit action-unit depth. For the estimator to be defined, the relevant window must satisfy: $S_{gross} (I) > 0$ , $S_{net} (I) > 0$ , $0 \leq W_{obs} (I) < S_{gross} (I)$ , and $N (I) \geq S_{gross} (I)$ .

Both partitions of the channel divide the same fixed $N (I)$ ; they differ only in whether the invalidated closures are counted as closures (baseline) or as load (net estimator).

Invalidation monotonicity theorem

The increase in effective question depth due to observable invalidation load is defined as the difference between the net operational estimator and the no-observable-invalidation baseline of equation (4):

{\hat{ΔKTD}}_{W}^{1bit} (I) := {\hat{KTD}}_{eff}^{1bit,net} (I) - {\hat{KTD}}_{base}^{1bit} (I) .

Substituting equations (4) and (5) gives:

${\hat{ΔKTD}}_{W}^{1bit} (I) = N (I) (\frac{1}{S_{net} (I)} - \frac{1}{S_{gross} (I)}) .$

Using $S_{net} (I) = S_{gross} (I) - W_{obs} (I)$ , this becomes:

${\hat{ΔKTD}}_{W}^{1bit} (I) = N (I) \frac{W_{obs} (I)}{S_{gross} (I) (S_{gross} (I) - W_{obs} (I))} .$

Equivalently:

${\hat{ΔKTD}}_{W}^{1bit} (I) = N (I) \frac{W_{obs} (I)}{S_{gross} (I) S_{net} (I)} = N (I) \frac{W_{obs} (I)}{(S_{net} (I) + W_{obs} (I)) S_{net} (I)}$

Theorem 1 — Invalidation monotonicity. Fix $N (I)$ and $S_{gross} (I)$ with $N (I) \geq S_{gross} (I) > 0$ . Regard the invalidation-induced increase in effective question depth as a function of the observable invalidation load $W = W_{obs} (I)$ on the domain $0 \leq W < S_{gross} (I)$ . Then on this domain the quantity ${\hat{ΔKTD}}_{W}^{1bit} (I)$ is (i) nonnegative, and equals zero if and only if $W = 0$ ; and (ii) strictly increasing in $W$ .

Proof. Write $G = S_{gross} (I)$ and $c = N (I) / G > 0$ , so that ${\hat{ΔKTD}}_{W}^{1bit} (I) = c \frac{W}{G - W}$ . At $W = 0$ the expression is zero, and it is positive for $W > 0$ , which yields (i). Differentiating $g (W) = W / (G - W)$ gives $g^{'} (W) = G / {(G - W)}^{2} > 0$ , which yields (ii).

Corollary 1 — Increasing marginal invalidation cost. For fixed $N (I)$ and $S_{gross} (I)$ , the invalidation-induced increase in effective question depth is strictly convex in $W$ .. Thus each additional invalidated closure has a larger marginal effect than the previous one.

Proof. The second derivative $g^{''} (W) = 2 G / {(G - W)}^{3} > 0$ on $0 \leq W < G$ is positive. Hence the invalidation burden grows faster than linearly as observable invalidation load increases.

This corollary is the operational amplification result. Invalidation does not merely subtract completed work. It reduces the denominator of surviving closures, so the same fixed channel capacity is spread over fewer accepted closures. The effective burden per surviving closure therefore rises nonlinearly with the invalidation fraction.

Theorem 1 is purely operational relative to A1–A5; it is a statement about the closed-form behavior of the accounting estimator alone. The convexity claim sharpens the earlier monotonicity remark — not only does each invalidated closure raise the effective question depth, but successive invalidations raise it by strictly increasing increments, because the surviving denominator $G - W$ shrinks as $W$ grows.

The interpretation is narrow and operational. Observable invalidation load does not directly measure internal entropy. It increases the effective one-bit question depth because the same fixed channel capacity is now amortized over fewer surviving closures. Some closure-fixing acts consumed capacity but did not remain accepted at the end of the window. This is a selection-equivalent debit, not a direct count of completed corrective rework.

Invalidation fraction form

The same result can be expressed in terms of the observable invalidation fraction:

w (I) := \frac{W_{obs} (I)}{S_{gross} (I)} .

Since $S_{net} = S_{gross} (1 - w)$ , equation (5) becomes:

{\hat{KTD}}_{eff}^{1bit,net} (I) + 1 = \frac{{\hat{KTD}}_{base}^{1bit} (I) + 1}{1 - w (I)} .

Therefore:

{\hat{ΔKTD}}_{W}^{1bit} (I) = ({\hat{KTD}}_{base}^{1bit} (I) + 1) \frac{w (I)}{1 - w (I)} .

This form exposes the amplification mechanism. As the invalidation fraction approaches one, the effective burden per surviving closure grows without bound. Operationally, this means that a process may consume large amounts of channel capacity while producing very few surviving closures.

Ideality assumptions

The operational estimator becomes an estimator of the latent Knowledge To Be Discovered only under explicit bridging assumptions. We collect them here so that every conditional claim below can name exactly which assumptions it requires. The accounting identities of the preceding subsections, and Proposition 1, hold unconditionally and do not depend on (B1)–(B4).

(B1) One-bit discrimination calibration The counted non-closure units are treated as one-bit-equivalent approximations to ideal binary discriminations about the required response-equivalence class X. A counted non-closure unit is therefore interpreted as an observable proxy for one response-relevant binary distinction, not as direct access to the regulator's internal posterior update.

This is the first assumption that ties the operational probe count of A5 to the latent knowledge-ledger layer. The dichotomy narrowing steps counted by A5 act on the concrete candidate set $C_{i}^{R} (d);$ the quantity of interest in the knowledge ledger is instead the ideal binary-question depth about the required response-equivalence class X, where X ranges over the class-projected candidate set $C_{i}^{X} = g_{t} [C_{i}^{R}]$ . B1 asserts that the A5 probe count is a calibrated proxy for that ideal question depth: each counted narrowing step is read as standing in for one ideal yes/no question about X, with the residual mismatch absorbed into the aggregate calibration error

Let the aggregate calibration error over window I be:

ϵ_{c a l} (I) := {\hat{K T D}}_{b a s e}^{1 b i t} (I) - {\bar{E}}_{I, n e t} [q^{*}] .

Here, ${\hat{K T D}}_{b a s e}^{1 b i t} (I)$ is the observed fixed-gross one-bit baseline, while ${\bar{E}}_{I, n e t} [q^{*}]$ is the average ideal binary-question depth over the net surviving closure population. Thus, $ϵ_{c a l} (I)$ measures the gap between the operational one-bit proxy and the ideal binary-question benchmark.

If $ϵ_{c a l} (I) = 0$ , the operational baseline is exactly calibrated to the ideal binary-question benchmark.
If $ϵ_{c a l} (I) > 0$ , the operational count overstates the ideal binary-question depth.
If $ϵ_{c a l} (I) < 0$ , the operational count understates the ideal binary-question depth.

B1 does not claim the two are identical. The mismatch it absorbs has a definite operational source: the concrete search may split the candidate set more finely than the class structure requires. When several surviving concrete responses lie in the same response-equivalence class, narrowing among them costs probes (raising Q) without resolving any question about X, so the operational count overstates ideal question depth and $ϵ_{c a l} (I) > 0$ . Conversely, a single probe that happens to cut cleanly across class boundaries may resolve class-uncertainty faster than its one-step charge suggests, giving $ϵ_{c a l} (I) < 0$ . Exact calibration, $ϵ_{c a l} (I) = 0$ , is the case in which the concrete-response search and the ideal class-question inquiry have the same depth on the surviving population.

This is not, by itself, a claim that every unobserved internal staged selection U_i contributes exactly one bit of conditional mutual information about X. The latter would be a stronger white-box idealization. Under that stronger idealization, if an episode has k_u information-bearing stages, each contributing one bit, and terminates with zero residual uncertainty, then $H_{u}^{start,real} = k_{u}$ . The operational estimator does not assume direct access to those stages. It uses counted non-closure action units as an observable one-bit-equivalent proxy, and its interpretation as latent KTD depends on the explicit bridging assumptions and the derived error envelope.

(B2) No hidden selection at closure. Each closure unit records only the externally visible episode-closing commitment and folds no uncounted response-relevant discrimination into that commitment.

(B3) Unit-debit invalidation. Each invalidated gross closure is charged as one closure-unit of consumed capacity that failed to survive. For comparison with the one-bit action-unit channel, this lost closure unit is represented as a one-bit-equivalent operational debit. This is not a claim that invalidation directly adds one bit of latent entropy. Equivalently, the invalidation debit is exactly the observed invalidation load, so that $Q_{eff} = Q + W_{obs}$ .

(B4) Population matching. The counted closure population coincides with the knowledge-ledger row population for the window, so that aggregate channel quantities and the latent average in equation (2) are taken over the same closures.

Relation between the operational estimator and latent KTD

The operational estimator and the latent Knowledge To Be Discovered estimand should be read in two layers.

First, the unconditional operational layer: ${\hat{KTD}}_{eff}^{1bit,net} (I)$ is the observed average effective one-bit action-unit depth per net surviving closure. This follows from the operational coding convention and the fixed-capacity accounting identity. It does not require direct access to the regulator's internal probability model.

Second, the conditional information-theoretic layer: the operational estimator becomes interpretable as an estimator of latent Knowledge To Be Discovered only through an explicit calibration bridge between counted non-closure units and ideal binary discriminations about the required response-equivalence class. The counting model alone does not derive that bridge.

Under the B1 assumption, the counted non-closure units are treated as one-bit-equivalent approximations to ideal binary discriminations. The mismatch between the operational baseline and the ideal binary-question benchmark is represented by the calibration error:

ϵ_{c a l} (I) := {\hat{K T D}}_{b a s e}^{1 b i t} (I) - {\bar{E}}_{I, n e t} [q^{*}] .

Thus:

{\hat{K T D}}_{b a s e}^{1 b i t} (I) = {\bar{E}}_{I, n e t} [q^{*}] + ϵ_{c a l} (I) .

Here, ${\bar{E}}_{I, net}^{} [q^{⋆}]$ is the average ideal binary-question depth over the net surviving closure population. If $ε_{cal} (I) = 0$ , the operational baseline is exactly calibrated to the ideal binary-question benchmark. If it is positive, the operational count overstates ideal question depth. If it is negative, the operational count understates ideal question depth.

Lemma 1 gives the remaining source-coding gap between ideal binary-question depth and latent realized Knowledge To Be Discovered. Define:

δ (I) := {\bar{E}}_{I, n e t} [q^{*}] - K T D_{a v g}^{s t a r t - r e a l, n e t} (I) .

By the one-bit coding bracket:

0 \leq δ (I) < 1.

The calibration error $ε_{cal} (I)$ and the coding gap $δ (I)$ are different quantities. The first measures operational miscalibration. The second is the standard sub-one-bit gap between entropy and optimal binary-question depth.

Theorem 2 — Operational-to-latent error envelope. Assume A1–A5 and B1–B4, with the fixed-gross baseline of equation (4) and $S_{gross} (I) > 0, S_{net} (I) > 0, 0 \leq W_{obs} (I) < S_{gross} (I) .$ .

Combining this exact operational decomposition with the calibration bridge and the one-bit coding bracket gives:

{\hat{K T D}}_{e f f}^{1 b i t, n e t} (I) - K T D_{a v g}^{s t a r t - r e a l, n e t} (I) = Δ {\hat{K T D}}_{W}^{1 b i t} (I) + ϵ_{c a l} (I) + δ (I), 0 \leq δ (I) < 1.

Equivalently, the operational-to-latent error envelope is:

$Δ {\hat{K T D}}_{W}^{1 b i t} (I) + ϵ_{c a l} (I) \leq {\hat{K T D}}_{e f f}^{1 b i t, n e t} (I) - K T D_{a v g}^{s t a r t - r e a l, n e t} (I) < Δ {\hat{K T D}}_{W}^{1 b i t} (I) + ϵ_{c a l} (I) + 1.$

(6)

If the calibration error is not known exactly but is bounded by:

| ϵ_{c a l} (I) | \leq ε,

then the calibration-robust envelope is:

Δ {\hat{K T D}}_{W}^{1 b i t} (I) - ε \leq {\hat{K T D}}_{e f f}^{1 b i t, n e t} (I) - K T D_{a v g}^{s t a r t - r e a l, n e t} (I) < Δ {\hat{K T D}}_{W}^{1 b i t} (I) + 1 + ε .

In the exactly calibrated special case, $ε_{cal} (I) = 0$ , the envelope reduces to:

Δ {\hat{K T D}}_{W}^{1 b i t} (I) \leq {\hat{K T D}}_{e f f}^{1 b i t, n e t} (I) - K T D_{a v g}^{s t a r t - r e a l, n e t} (I) < Δ {\hat{K T D}}_{W}^{1 b i t} (I) + 1.

Proof. The exact operational decomposition follows from equations (4) and (5):

{\hat{K T D}}_{e f f}^{1 b i t, n e t} (I) - {\hat{K T D}}_{b a s e}^{1 b i t} (I) = Δ {\hat{K T D}}_{W}^{1 b i t} (I) .

This step uses only the operational accounting identity and the definition of the invalidation debit. It does not require an entropy interpretation.

By B1, the fixed-gross baseline differs from the average ideal binary-question depth by the calibration error:

{\hat{K T D}}_{b a s e}^{1 b i t} (I) = {\bar{E}}_{I, n e t} [q^{*}] + ϵ_{c a l} (I) .

By Lemma 1, the average ideal binary-question depth differs from the latent realized average starting Knowledge To Be Discovered by a coding gap:

{\bar{E}}_{I, n e t} [q^{*}] = K T D_{a v g}^{s t a r t - r e a l, n e t} (I) + δ (I), 0 \leq δ (I) < 1.

Substituting these two relations into the exact operational decomposition yields:

{\hat{K T D}}_{e f f}^{1 b i t, n e t} (I) = K T D_{a v g}^{s t a r t - r e a l, n e t} (I) + δ (I) + ϵ_{c a l} (I) + Δ {\hat{K T D}}_{W}^{1 b i t} (I) .

Rearranging gives:

{\hat{K T D}}_{e f f}^{1 b i t, n e t} (I) - K T D_{a v g}^{s t a r t - r e a l, n e t} (I) = Δ {\hat{K T D}}_{W}^{1 b i t} (I) + ϵ_{c a l} (I) + δ (I) .

Since $0 \leq δ (I) < 1$ , the stated envelope follows immediately. If only $| ε_{cal} (I) | \leq ϵ$ is known, substituting the worst-case bounds $- ϵ \leq ε_{cal} (I) \leq ϵ$ gives the calibration-robust envelope.

This proves the theorem. $□$

The theorem separates three effects. The operational invalidation debit ${\hat{ΔKTD}}_{W}^{1bit} (I)$ is exact and comes from the ledger. The calibration error $ε_{cal} (I)$ comes from the mismatch between counted non-closure units and ideal binary discriminations. The coding gap $δ (I)$ comes from the standard sub-one-bit source-coding bracket.

The envelope is not an empirical guarantee produced by the operational ledger alone. It is a conditional envelope: the operational ledger supplies the exact debit term; B1-B2 plus Lemma 1 supply the entropy bracket.

Combining the ledger identity and the selection-equivalent debit, define equation (5) as the operational counterpart to the latent realized average starting Knowledge To Be Discovered for surviving closures: Equation (5) is operationally exact by accounting. Its interpretation as an estimator of the latent information-theoretic quantity ${KTD}_{avg}^{start-real,net} (I)$ is conditional on the calibration quality captured by $ε_{cal} (I)$ . If the calibration bridge is weak, the equation remains a valid operational ratio, but its reading as an entropy estimator becomes a proxy claim rather than a derived identity.

Practical calibration procedure

The calibration procedure is a method for refining the action partition to improve the calibration of the operational estimator to the ideal binary-question benchmark. The procedure is iterative and data-driven, and it relies on the observed information increments in the action stream.

Let $Δ$ denote the temporal resolution at which action is segmented into action units for counting, and let $A_{i}^{Δ}$ denote the response-relevant action unit observed in the i-th time bin. The calibrated estimate is not obtained by summing the raw variety of isolated action bins. It is obtained by summing conditional information increments:

Ê_{Δ} (I) = Σ_{i} H (A_{i}^{Δ} | A_{< i}^{Δ}, C_{i}^{Δ})

where $C_{i}^{Δ}$ contains the context already available before the action in that bin, including prior body state, prior action, available sensory information, task constraints, and relevant disturbance state. This prevents biomechanical continuation or already-determined motion from being counted as new response knowledge.

The calibration residual is then:

ϵ_{c a l} (Δ, I) = {\hat{K T D}}_{Δ} (I) - {\bar{E}}_{I, n e t} [q *]

The residual is reduced by refining the action partition only when the refinement preserves response-relevant distinctions and removes irrelevant motor detail.

As the action segmentation becomes finer and the conditioning context becomes richer, the estimated discriminative entropy should converge toward the ideal response-selection entropy.

In the ideal calibration limit, admissible refinements converge to a stable entropy-rate estimate, so that:

lim_{Δ \to 0} ϵ_{c a l} (Δ, I) = 0

This limit should be read as a calibration condition, not as a consequence of smaller time bins alone.

Knowledge-Discovery Efficiency (KEDE) Metric

Now we generalize the Knowledge-Discovery Efficiency (KEDE) - scalar metric that quantifies how efficiently a system closes the gap between the variety demanded by its environment and the variety embodied in its prior knowledge[28].

We rearrange the formula (5) and insted of $\hat{H} (X | Y)$ we use $H (X | Y)$ for notation simplicity. and get the formula for Knowledge-Discovery Efficiency (KEDE) metric[28]:

$KEDE = \frac{1}{1 + H (X | Y)} = \frac{S - W}{N}$

(8)

KEDE is a scalar metric that quantifies how efficiently a system closes the gap between the variety demanded by its environment and the variety embodied in its prior knowledge[28]. KEDE is an acronym for KnowledgE Discovery Efficiency. It is pronounced [ki:d].

Efficiency means the smaller the average number of selections made per outcome the better. In other words - the less knowledge to be discovered per outcome the more efficient the knowledge discovery process is.

KEDE has the properties:

It is a function of the missing information H
Its maximum value corresponds to H equals zero i.e. there is no need to make selections, all knowledge is already discovered.
Its minimum value corresponds to H equals Infinity i.e. we have no knowledge to start with.
It is continuous in the closed interval of [0,1]. This makes it very useful to be used as a percentage. This is because we need to be able to rank knowledge discovery processes by efficiency. The best ranked knowledge discovery process will have 100% and the worst 0%. That is practical and people are used to having such a scale.

What does KEDE measure?

Regulation consumes execution capacity to cope with missing knowledge.
Knowledge discovery converts that consumed capacity into persistent internal variety, reducing future consumtion of the execution capacity.
KEDE measures the efficiency of this conversion: how much execution capacity is spent on discovery versus production, under a successful-adaptation regime.

KEDE effectively converts the knowledge to be discovered H(X|Y), which can range from 0 to infinity, into a bounded scale between 0 and 1.

KEDE is a measure of how much of the required knowledge for completing tasks is covered by the prior knowledge.

Due to its general definition KEDE can be used for comparisons between organizations in different contexts. For instance to compare hospitals with software development companies! That is possible as long as KEDE calculation is defined properly for each context. In what follows we will define KEDE calculation for the case of knowledge workers who produce textual content in general and computer source code in particular.

Anchoring KEDE to Natural Constraints

In our model, N is always the theoretical maximum action rate (selections + outcomes) in an unconstrained environment, and S is the observed outcome rate under specific conditions over a given interval.

A key question is how to assign a natural constraint to N. That is, what constitutes an appropriate reference value for the maximum action rate (selections + outcomes)?

We may turn to physics for an instructive analogy. A quantum (plural: quanta) represents the smallest discrete unit of a physical phenomenon. For instance, a quantum of light is a photon, and a quantum of electricity is an electron. In this context, the speed of light in a vacuum serves as a fundamental upper bound for N. However, identifying an analogous natural constraint for human activity—particularly knowledge work—presents greater challenges.

Consider the example of typing. Here, the quantum can reasonably be defined as a symbol, since it is the smallest discrete unit of text. A symbol may be a letter, number, punctuation mark, or whitespace character. To determine the appropriate bin width Δt, we refer to empirical data on the minimum time required to produce a single symbol. Typing speed has been subject to considerable research. One of the metrics used for analyzing typing speed is inter-key interval (IKI), which is the difference in timestamps between two keypress events. We see that IKI is defined equal to the symbol duration time t. Hence we can use the research of IKI to find the symbol duration time t. Studies have reported an average IKI of 0.238 seconds [26], yielding a maximum human typing rate of approximately N=1/t=1/0,238=4.2 symbols per second

A similar approach can be applied to tasks such as furniture assembly. In this case, a plausible quantum is a single screw tightened, since it represents a minimal, repeatable unit of outcome. We then identify Δt as the average time required to tighten one screw. Empirical studies report that this task typically takes between 5 and 10 seconds[34]. Using the upper bound, we estimate the maximum screw-tightening rate as N=1/t=1/10=0.1 screws per second.

This methodology offers a principled way to estimate N using domain-specific quanta and empirically grounded time durations, enabling the application of our model to a broad range of human tasks.

The next question concerns the appropriate definition of outcome for measuring S and N.

Both N and S can always be discretized—or “binned”—in a way that preserves the total information rate, regardless of whether the outcome arises from natural processes, human behavior, or machines. By choosing a bin width Δt small enough (e.g., milliseconds), the range of possible tangible outcomes within each bin shrinks dramatically. This reduced range leads to less uncertainty in each bin, which compensates for the smaller time interval. Yet the ratio

\frac{total outcome in bin}{Δt}

remains an accurate measure of information rate.

As Δt becomes smaller, the measurements of S and N become more precise, as they reflect outcome over finer time intervals. But how small should Δt be? This dilemma is resolved by considering the granularity of outcomes associated with the outcome. The set E of outcomes can be thought of as the effects of the regulation process — the resulting states after the regulator responds to disturbances. In our model E is a sequence of {0,1}, where 0 = wrong outcome(failure to regulate) and 1 = acceptable outcome. So the presence of a concrete outcome leads to a natural binning of the outcomes, It also enables a clear distinction between signal (the entropy associated with producing the outcome) and noise (the residual variability unrelated to success or failure).

For example, two distinct symbols typed (e.g., ‘a' vs. ‘b') are clearly different outcomes. However, if one symbol is typed in 91 milliseconds and another in 92 milliseconds, this minute variation is inconsequential to the outcome. Such timing fluctuations are typically unintentional, irrelevant to task performance, and should not be considered part of the outcome. In practical terms, if the theoretical upper bound N is known—for instance, 4.2 symbols per second as derived from human typing speed, and the observed rate is S=1 symbol per second, then time should be partitioned into one-second bins. Each bin then yields a single outcome: either 1 (a symbol was successfully typed) or 0 (no symbol typed or incorrect input).

This binning principle generalizes beyond typing. Whether analyzing foot strikes in trail running (where negligible spatial change occurs over milliseconds) or the discrete moves in solving a Rubik's cube (where each turn resolves multiple potential states into a single action), binning ensures that no intermediate state need be modeled explicitly.

Physical applicability claim. For any isolated physical system to which a finite entropy bound applies, the number of physically distinguishable states is finite. Therefore the system admits a binary encoding whose length is bounded by the corresponding entropy bound expressed in bits. In holographic settings, this gives an upper bound of $N = \frac{A}{4 {l_{p}}^{2} \ln (2)}$ binary discriminations. Here they use the Planck length $l_{p} = {(\frac{ℏ G}{c^{3}})}^{1 / 2} m$ meters) and its associated surface area, the Planck area ${l_{p}}^{2} = \frac{ℏ G}{c^{3}}$ . Hence the Knowledge To Be Discovered Estimator applies to such physical systems after representing admissible states by a bounded sequence of binary discriminations.

Applications

The knowledge-centric perspective builds on Ashby's Law of Requisite Variety by emphasizing that successful outcomes depend not only on a system's range of possible responses, but also on its ability to select the right response for each disturbance. This requires internal “system knowledge” that maps disturbances to appropriate actions. As Francis Heylighen proposed in his “Law of Requisite Knowledge,” effective regulation demands more than variety—it demands informed selection[29]. This knowledge-centric lens provides a foundation for analyzing how systems—biological, technical, or organizational—achieve control not just through options, but through understanding. The model we present operationalizes this perspective by estimating the informational requirements a system must satisfy to achieve its observed level of regulatory performance.

In what follows, we apply this knowledge-centric perspective to a range of domains, including motor tasks and manual assembly, industrial assembly lines, software development processes, speed of light in a medium, intelligence testing and sports performance. In each case, the model enables us to estimate, in bits of information, the amount of knowledge a system must lack to produce its observed level of performance. By quantifying the knowledge to be discovered H(X|Y), we assess how much uncertainty was there in the system's ability to select appropriate responses. This allows us to compare systems not by tangible outcomes, but by the hidden knowledge structures required to achieve them, offering a unified lens for analyzing adaptation, skill, and control across diverse contexts.

Tightening screws

We can apply our model to motor tasks such as furniture assembly. In this context, a natural unit of outcome — or “quantum” — is the tightening of a single screw.

Skilled workers engaged in manual assembly tasks can typically insert and tighten standard screws at a rate of 6'-12 screws per minute under optimal, repetitive conditions — such as those found in furniture construction or industrial assembly lines. In contrast, automated screw-tightening machines can achieve significantly higher rates, often between 30 and 60 screws per minute [34] More complex manual tasks, such as high-torque applications involving ratchets or Allen keys, typically reduce the rate to 2'-4 screws per minute due to the increased effort and precision required. In surgical or medical contexts, such as orthopedic screw insertion, accuracy and the avoidance of overtightening are paramount; here, rates often fall to 1'-2 screws per minute, or approximately one screw every 30'-60 seconds [46].

Context	Typical Rate (screws/minute)	Notes
Automated (machine)	30'-60	For comparison, not manual
Fast, repetitive tasks	6'-12	Assembly line, minimal torque required
High-torque/manual	2'-4	Metalwork, ratchets, Allen keys
Surgical/precision	1'-2	Orthopedic, high accuracy, low speed

The key observation is that rates decrease as torque, task complexity, or required precision increases. If we take the machine rate as the maximum possible outcome N and the observed human rate as S, we can estimate the average number of bits of information H(X|Y) that the human operator must process per action.

KEDE = \frac{S}{N}

H (X | Y) = \frac{1}{KEDE} - 1 = \frac{N}{S} - 1 = \frac{60}{12} - 1 = 4 b i t s / s c r e w

This implies that the human must absorb approximately 4 bits of information, on average, to tighten a single screw under typical conditions.

The rate at which a person tightens screws depends on various factors, including:

Screw type and size
Material being fastened
Required torque
Tool used (screwdriver, ratchet, etc.)
Operator skill and fatigue

These constitute the disturbance variety D faced by the human operator. The operator, acting as a regulator, responds with selections from their internal repertoire of skills — the regulatory variety R.

This interpretation aligns with existing research, which suggests that task difficulty directly influences the amount of information a task imparts [47, 48]. When difficulty is appropriately matched to the individual's skill level, the task yields maximal informational value [49], and the time required reflects the interaction between task complexity and the individual's regulatory capacity [50].

Using our model, we transform a sequence of real-world actions in furniture assembly into a granular, time-based measure of regulatory capacity. This enables us to quantify — in bits — how much variety the individual must absorb in order to successfully complete the task.

Typing the longest English word

Let's use an example scenario to see Ashby's law applied to human cognition and knowledge work.

For that we'll have myself executing the task of typing on a keyboard the word “Honorificabilitudinitatibus”. It means “the state of being able to achieve honours” and is mentioned by Costard in Act V, Scene I of William Shakespeare's “Love's Labour's Lost”. With its 27 letters “Honorificabilitudinitatibus” is the longest word in the English language featuring only alternating consonants and vowels.

The way I will execute this task is to go to the "play text" or "script" of “Love's Labour's Lost”, look up the word and type it down. The manual part of the task is to type 27 letters. The knowledge part of the task is to know which are those 27 letters.

In order to track the knowledge discovery process I will put "1" for each time interval when I have a letter typed and "0" for each time interval when I don't know what letter to type.

I start by taking a good look at the word “Honorificabilitudinitatibus” in the script of “Love's Labours' Lost”. That takes me two time intervals. Then I type the first letters “H”, “o”, and “n”.I continue typing letter after letter: “o”, “r”. At this point I cannot recall the next letter. What should I do? I am missing information so I go and open up the script of “Love's Labours Lost” and I look up the word again. Now I know what the next letter to type is but acquiring that information took me one time interval. This time I have remembered more letters so I am able to type “i”,”f”,”i”,”c”,”a”,”b”,”i”. Then again I cannot continue because I have forgotten what were the next letters of the word, so I have to look it up again.in the script. That takes two more time intervals. Now I can continue my typing of “l”,”i”,”t”. At this point I stop again because I am not sure what were the next letters to type, so I have to think about it. That takes one time interval. I continue my typing with “u”,”d”,”i”. Then I stop again because I have again forgotten what were the next letters to type, so I have to look it up again in the script of “Love's Labours Lost”. That takes two more time intervals. Now I know what the next letter to type is so I can continue typing “n”,”i”.At this point I cannot recall the next letter. so I have to look it up again in the script. That takes two more time intervals. After I know what the next letter to type is I can continue typing “t”,”a”,”t”,”i”,”b”,”u”,”s”. Eventually I am done!

At the end of the exercise I have the word “Honorificabilitudinitatibus” typed and along with it a sequence of zeros and ones.

		H	o	n	o	r		i	f	i	c	a	b	i			l	i	t		u	d	i			n	i			t	a	t	i	b	u	s
0	0	1	1	1	1	1	0	1	1	1	1	1	1	1	0	0	1	1	1	0	1	1	1	0	0	1	1	0	0	1	1	1	1	1	1	1

In the table we have separated the manual work of typing from the knowledge work of thinking about what to type.

We made visible both the manual work and the knowledge discovery parts of a Knowledge Discovery process.

The first row of the table shows the knowledge I manually transformed into tangible outcome - in this case the longest English word. The second row of the table shows the way I discovered that knowledge. There is a "0" for each time interval when I was missing information about what to type next. There is "1" for each time interval when I had prior knowledge about what to type next. Each "0" represents a selection I needed to ask in order to acquire the missing information about what letter to type next. Each "1" represents prior knowledge.

We know that there is knowledge applied when we see the tangible outcome of the process. We know there was knowledge discovered when we see there was at least one selection made.

In the exercise above we witnessed the discovery and transformation of invisible knowledge into visible tangible outcome.

KEDE calculation

We can calculate the KEDE for this sequence of outcomes.

KEDE = \frac{S}{N} = \frac{27}{37} = 0.73

We can also calculate the knowledge discovered H(X|Y) in bits of information.

H (X | Y) = \frac{N}{S} - 1 = \frac{37}{27} - 1 = 0.37

We've turned a real-world sequence of action and hesitation into a fine-grained, time-based measurement of regulatory capacity — effectively measuring how much variety I needed to absorb with external help i.e. my knowledge discovered.

Measuring software development

In order to use the KEDE formula (8) in practice we need to know both S and N. We can count the actual number of symbols of source code contributed straight from the source code files. For N we want to use some naturally constrained value.

N is the maximum number of symbols that could be contributed for a time interval by a single human being.

In the below formula for N we want to use some naturally constrained value: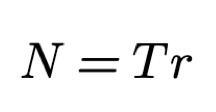

To achieve this, the following estimation is performed. We pick T = 8 hours of work because that is the standard length of a work day for a software developer.

To calculate the value of r we need to pick the symbol duration t.

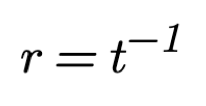
The value of the symbol duration time t is determined by two natural constraints:

the maximum typing speed of human beings
the capacity of the cognitive control of the human brain

Typing speed has been subject to considerable research. One of the metrics used for analyzing typing speed is inter-key interval (IKI), which is the difference in timestamps between two keypress events. We see that IKI is defined equal to the symbol duration time t. Hence we can use the research of IKI to find the symbol duration time t. It was found that the average IKI is 0.238s [26]. There are many factors that affect IKI [6]. It was also found that proficient typing is dependent on the ability to view characters in advance of the one currently being typed. The median IKI was 0.101s for typing with unlimited preview and for typing with 8 characters visible to the right of the to-be-typed character but was 0.446s with only 1 character visible prior to each keystroke [7]. Another well-documented finding is that familiar, meaningful material is typed faster than unfamiliar, nonsense material[8]. Another finding that may account for some of the IKI variability is what may be called the “word initiation effect”. If words are stored in memory as integral units, one may expect the latency of the first keystroke in the word to reflect the time required to retrieve the word from memory[55].

Cognitive control, also known as executive function, is a higher-level cognitive process that involves the ability to control and manage other cognitive processes that permit selection and prioritization of information processing in different cognitive domains to reach the capacity-limited conscious mind. Cognitive control coordinates thoughts and actions under uncertainty. It's like the "conductor" of the cognitive processes, orchestrating and managing how they work together. Information theory has been applied to cognitive control by studying the capacity of cognitive control in terms of the amount of information that can be processed or manipulated at any given time. Researchers found that the capacity of cognitive control is approximately 3 to 4 bits per second[32][33], That means cognitive control as a higher-level function has a remarkably low capacity.

Based on the above research we get:

Maximum typing speed of human beings to be r=1/t=1/0,238=4.2 symbols per second
Capacity of the cognitive control of the human brain to be approximately 3 to 4 bits per second. Since we assume one question equals one bit of information we get 3 to 4 questions per second.
Asking questions is an effortful task and humans cannot type at the same time. If there was a symbol NOT typed then there was a question asked. That means the question rate equals the symbol rate, as explained here.

Since the question rate needs to equal the symbol rate we consider that 4.2 symbols per second is a rate higher than 3 to 4 bits per second. We need to get a symbol rate between 3 and 4 symbols per second.

In order to get a round value of maximum symbol rate N of 100 000 symbols per 8 hours of work we pick symbol duration time t to be 0.288 seconds. That is a bit larger than what the IKI research found but makes sense when we think of 8 hours of typing. Having t of 0.288 seconds makes a symbol rate r of 3.47 symbols per second. That is between 3 and 4 and matches the capacity of the cognitive control of the human brain.

We define CPH as the maximum rate of characters that could be contributed per hour. Since r is 3.47 symbols per second we get CPH of 12 500 symbols per hour. We substitute T = h and r=CPH and the formula for N becomes:

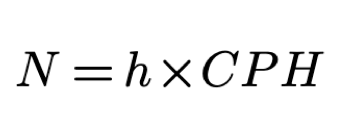
where h is the number of working hours in a day and CPH is the maximum number of characters that could be contributed per hour. We define h to be eight hours and get N to be 100 000 symbols per eight hours of work.

Total working time consist of four components:

Time spent typing (coding)
Time spent figuring out WHAT to develop
Time spent figuring out HOW to code the WHAT
Time doing something else (NW)

Let us assume an ideal system where the time spent doing something else T_NW is zero. Using the new formula for N the formula for H becomes

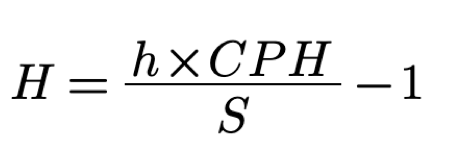
Note, that since N is calculated per hour so S also needs to be counted in an hour.

We see that the more symbols of source code contributed during a time interval the less missing information was there to be acquired. We want to compare the performance of different software development processes in terms of the efficiency of their knowledge discovery processes. Hence we rearrange the formula to emphasize that.

$\frac{S}{h \times C P H} = \frac{1}{1 + H}$

(8)

The right hand part is the KEDE we defined earlier. Thus, we define an instance of the metric KEDE - the general metric that we introduced earlier. This version of KEDE is for the case of knowledge workers that produce tangible outcome in the form of textual content:

$KEDE = \frac{S}{h \times C P H}$

(9)

KEDE from (9) contains only quantities we can measure in practice. KEDE also satisfies all properties we defined earlier. it has a maximum value of 1 and minimum value of 0; it equals 0 when H is infinite; it equals 1 when H is zero; it is anchored on a natural constraint—the maximum typing speed of a human being.

If we convert the KEDE formula into percentages then it becomes:

$KEDE = \frac{S}{h \times C P H} \times 100 %$

(10)

We can use KEDE to compare the knowledge discovery efficiency of software development organizations.

Testing Intelligence

Today all measure intelligence by the power of appropriate selection (of the right answers from the wrong). The tests thus use the same operation as is used in the theorem on requisite variety, and must therefore be subject to the same limitation. (D, of course, is here the set of possible questions, and R is the set of all possible answers). Thus what we understand as a man's “intelligence” is subject to the fundamental limitation: it cannot exceed his capacity as a transducer. (To be exact, “capacity” must here be defined on a per-second or a per-question basis, according to the type of test.)[3]

We can also use our model to the testing of human and AI intelligence. We infer this capacity from performance under variety — i.e., how many different problems a system or a person can solve correctly.

The dominant mathematical models for testing intelligence by the number of answered problems are benchmark datasets like MMLU, GSM8K, MATH, and FrontierMath. These models measure intelligence by the raw count or percentage of correctly solved problems, with more advanced benchmarks designed to minimize guessing and require deep reasoning.

From the knowledge-centric perspective:

The disturbances are the questions $Q = {q_{1}, q_{2}, q_{3}, . . . q_{n}}$
The person gives responses $R = {r_{1}, r_{2}, r_{3}, . . . r_{n}}$
The outcomes are $E = {e_{1}, e_{2}, e_{3}, . . . e_{n}} \in {0, 1}$

So: Intelligence is the capacity to consistently produce 1s in E, despite the variety in D.

Several mathematical models and benchmark datasets are used to evaluate intelligence—especially artificial intelligence (AI)—by measuring the number and complexity of math problems answered correctly. These models serve as standardized tests for both AI and, by analogy, human intelligence[52].

Massive Multitask Language Understanding (MMLU):

MMLU is a widely used benchmark that tests AI models on a broad range of subjects, including mathematics at various levels (high school, college, abstract algebra, formal logic).
The test is typically formatted as multiple-choice questions, and performance is measured by the percentage of correct answers out of the total number of questions
For example, advanced AI models have achieved up to 98% accuracy on math sections of MMLU, indicating high proficiency in standard math tasks but not necessarily deep reasoning

Grade School Math 8K (GSM8K)

GSM8K is a dataset of 8,500 high-quality, grade school-level word problems designed to test logical reasoning and basic arithmetic skills.
Evaluation is based on exact match accuracy: the number of problems answered exactly correctly divided by the total number attempted
This benchmark is used to assess step-by-step reasoning and the ability to handle linguistic diversity in problem statements.

MATH (Mathematics Competitions Dataset)

MATH consists of problems from high-level math competitions (e.g., AMC 10, AMC 12, AIME), focusing on advanced reasoning rather than rote computation.
Performance is measured by the percentage of correct answers, with human experts (e.g., IMO medalists) providing a reference for top-level performance
The dataset is challenging for both humans and AI, with LLMs typically scoring much lower than expert humans.

FrontierMath[53]

FrontierMath is a new benchmark featuring hundreds of original, expert-level math problems spanning major branches of modern mathematics.
Problems are designed to be "guessproof" and require genuine mathematical understanding, with automatic verification of answers
The benchmark is used to assess how well AI models can understand and solve complex mathematical problems, similar to human performance.

In human intelligence testing, Psychometric models such as IQ tests or psychometric approaches also use the number of correctly answered problems as a key metric. These tests are standardized, and the raw score (number of correct answers) is often converted into a scaled score or percentile.

As an example we will use the Exact Match metric as the evaluation method[52]. Given that each question in our benchmark dataset has a single correct answer and the model produces a response per query, Exact Match ensures a rigorous evaluation by comparing the extracted answer to the ground truth.

Let $ŷ_{i}$ represent the extracted answer from the model's outcome for the $i^{th}$ question, and let $y_{i}$ be the corresponding ground truth answer. The Exact Match accuracy is computed as:

$Exact Match (%) = \frac{\sum_{i = 1}^{N} 𝟙 (normalize (ŷ_{i}) = normalize (y_{i}))}{N} x 100$

where:

$N$ is the total number of evaluated questions.
$𝟙 (\cdot)$ is the indicator function, returning 1 if the extracted model response matches the ground truth after preprocessing, and 0 otherwise.
$normalize (\cdot)$ is a function that standardizes formatting, trims spaces, and normalizes numerical values.

The knowledge discovery efficiency of an LLM can be calculated as:

Exact Match accuracy = \frac{S}{N} = KEDE

where S is the number of correct answers and N is the total number of evaluated questions..

Let's pick the case of the performance of GPT-4o on the MATH benchmark, which achieved a significantly lower accuracy of 64.88%, lagging behind its peer models[52]. Now, we can calculate the average knowledge discovered H(X|Y).

H (X | Y) = \frac{1}{KEDE} - 1 = \frac{100}{64.88} - 1 = 1.54 b i t s / problem

Basketball Game

We can also use this model to assess the performance of a basketball player.

Timeframe is a basketball game.
We observe N total shot attempts.
S of them are successful (shot made).
We record a binary outcome sequence
$E \in {0, 1}^{N}$
The empirical success rate:
$θ = \frac{S }{N}$
is our observed probability of success.

Interpretation using Ashby's Law

The basketball shot is a regulation problem: the player must control their body and respond to the game environment to produce the desired outcome. The player is faced with a series of disturbances (D) in the form of different shots to make under different conditions. The player responds with a selection, drawn from their internal skills (regulatory variety R) in the form of different shooting techniques. Each shot is uncertain whether it will be successful. The outcome E is whether the shot is made (2) or missed (0).

Over N shots, the success rate

θ = \frac{S ​}{N}

reflects how often the player's internal variety is sufficient to absorb the variety in the environment — an operational measure of regulatory success.

In this case, θ becomes a practical proxy for how often the regulator (player) has sufficient internal variety to absorb the disturbance presented by the game. However, it is important to note that this is a simplified model and does not account for all the complexities of basketball performance. For example, the player may have different success rates depending on the type of shot, the position on the court, or the level of defense. These factors can all affect the player's ability to regulate their performance and should be considered when interpreting the results. Thus, as explained here θ is a useful heuristics for P(E=1), but the full picture includes the quality of mapping, not just quantity.

Applying the Model

NBA keeps track of field goal attempts and makes for each player. The most field goal attempts by a player in a single NBA game is 63, achieved by Wilt Chamberlain during his legendary 100-point game against the New York Knicks on March 2, 1962 We take this as the natural constraint so N=63. We can also take the number of successful shots S=36, which is the most field goals made in a single game by a player[13].

We can calculate the KEDE for this sequence of outcomes.

KEDE = \frac{S}{N} = \frac{36}{63} = 0.571

We can also calculate the knowledge discovered H(X|Y) in bits of information.

H (X | Y) = \frac{N}{S} - 1 = \frac{63}{36} - 1 = 0.75

That means that the player needed to absorb 0.75 bits of information on average to make the shot.

We've turned a real-world sequence of basketball shots into a fine-grained, time-based measurement of a regulatory capacity — effectively measuring how much variety the player needed to absorb.

We can also use this model to assess the performance of a basketball team. In this case the success rate coincides with the field goal percentage (FG%) of the team which is the percentage proportion of made shots over total shots that a player or a team takes in games. There is a statistical distribution for NBA field goal percentage (FG%) [10]. Analysts and researchers often study the distribution of FG% across players or teams to understand scoring efficiency and trends[11]. The NBA record for the highest FG% in a single game by a team is 69.3%, set by the Los Angeles Clippers on March 13, 1998, when they made 61 of 88 shots[12].

For example, in the 2023-24 season, team FG% ranged from about 43.5% (lowest) to 50.6% (highest), with the league average typically falling in the mid-to-high 40% range[11]. if we take the average FG% of 45% , we can calculate the average knowledge discovered H(X|Y).

H (X | Y) = \frac{1}{KEDE} - 1 = \frac{1}{F G %} - 1 = \frac{1}{0.45} - 1 = 1.22

That means that a team needed to absorb 1.22 bits of information on average to make a shot.

Assembly Line

We can also use this model to assess the knowledge discovery efficiency of an assembly line.

The assembly line is a system that transforms raw materials into finished products. The assembly line has a set of disturbances (D) in the form of different raw materials, machines, and processes. The assembly line responds with a selection, drawn from its internal structure (R) in the form of different machines, processes, and workers.

From a knowledge-sentric perspective most of the knpwledge discovery happens in the design phase of the assembly line. This is the planning for design, fabrication and assembly. This activity has also been called design for manufacturing and assembly (DFM/A) or sometimes predictive engineering. It is essentially the selection of design features and options that promote cost-competitive manufacturing, assembly, and test practices[51]. Thus most of the disturbances D are already absorbed by the design of the assembly line. That means when the workers have most of the knowledge built into the assembly line and the operational procedures.

Assembly line efficiency (AE) is the ratio of the outcome to the maximum possible outcome, often expressed as a percentage.

The efficiency of the assembly line can be calculated as:

AE = \frac{S}{N} = KEDE

where S is the actual outcome and N is the maximum possible outcome.

We can assume that an assembly line is designed to produce a certain number of successful products (S) with a maximum rate of N products per hour. So for example, a shoe manufacturer has an actual outcome of 100 shoes per day, and a maximum potential outcome of 120 shoes per day. Their production line efficiency would be 83%. Now, we can calculate the average knowledge discovered H(X|Y).

H (X | Y) = \frac{1}{KEDE} - 1 = \frac{1}{A E} - 1 = \frac{100}{83} - 1 = 0.2 b i t s / s h o e

To optimize the AE, companies can apply DFA guidelines, such as minimizing the number and variety of parts, standardizing the fasteners and connectors, and simplifying the assembly sequence and orientation[51].

Interpreting the results involves a comprehensive analysis of the data to understand where and why inefficiencies occur. In general, the higher the AE, the better the design. On the other hand, AE close to 100% might indicate under-utilised capacity. It's essential to compare high efficiency with industry capacity standards to determine if an increase in production is feasible and beneficial.

If AE is consistently below industry benchmarks, this could highlight several potential issues:

Machinery: It may indicate that machines are outdated, malfunctioning, or not suitable for the required tasks.
Labour Skills: Low efficiency might be due to workforce training gaps.
Process Design: Sometimes, the workflow or layout of the production line itself causes inefficiencies.

Speed of Light in Medium

We can also use this model to support an interpretation of Ashby's Law of Requisite Variety to assess the speed of light in a medium where the medium acts as a disturbance to photon flow. Here's how this perspective aligns with the physics of light-matter interactions:

Disturbance: The medium's atomic/molecular structure introduces spatial and electromagnetic inhomogeneities (e.g., refractive index variations, turbulence).
Control Mechanism: Photons' ability to "counteract" disturbances through wavelength compression and phase synchronization.
Requisite Variety: Photons require sufficient adaptability (e.g., frequency range, polarization states) to navigate the medium's complexity without scattering or losing coherence.

The speed of light in a vacuum is 299,792,458 m/s. In a medium, the speed of light is reduced by a factor n, called the refractive index defined as:

n = \frac{c}{v}

where c is the speed of light in vacuum and v is the speed of light in the medium.

The refractive index is a measure of how much the speed of light is reduced in the medium. The higher the refractive index, the more the speed of light is reduced.

For example, the refractive index of water is 1.33, which means that the speed of light in water is:

v = \frac{299 792 458}{1.33} \approx 225 000 000 m / s

The knowledge discovery efficiency of the speed of light in a medium can be calculated as:

KEDE = \frac{v}{c} = \frac{1}{n}

where v is the actual speed of light in the medium and c is the maximum possible speed of light in vacuum.

Now, we can calculate the average knowledge discovered H(X|Y) by a photon in water:

H (X | Y) = \frac{1}{KEDE} - 1 = \frac{1}{\frac{1}{n}} - 1 = n - 1 = 1.33 - 1 = 0. 33 b i t s / p h o t o n

Appendix

Example: A Two-Dimensional Parabola

Consider the parabola as an example of the distinction between a variable, the set of its possible values, the set of realized values, and the graph of a mapping.

Let D be the disturbance variable, and let its set of possible values be

D = R

Let Z be the outcome variable, with possible outcome-values

Z = R_{\geq 0}

and define the realized outcome map by

z_{ρ} : D \to Z

z_{ρ} (d) = d^{2}

The parabola is then the graph

G = {(d, z) \in D \times Z : z = d^{2}}

Thus:

the x-axis contains disturbance-values $d \in D$
the y-axis contains outcome-values $z \in Z$
the parabola itself is the graph of the map $z_{ρ} (d)$

Distinct disturbance-values may yield the same outcome-value:

z_{ρ} (- 2) = 4, z_{ρ} (2) = 4

The repetition belongs to the mapping, not to the set 𝒴. The set of possible outcome-values still contains the value 4 only once.

Where are $E$ and its acceptable subset η?

The essential-value space $E$ appears only once one specifies how outcomes are evaluated. There are two natural cases:

Case 1: The y-axis already represents the essential values

If the outcome-values themselves are the essential values, then

E = Z

and the evaluation map is simply the identity:

φ : Z \to E, φ (z) = z

In that case, E is represented directly by the y-axis and the acceptable subset is literally a subset of the y-axis. For example,

η = [0, 4] \subseteq E

Geometrically, η is the allowed vertical segment on the y-axis.

Then the question of successful regulation becomes: $z_{ρ} [D] \subseteq η$

If $D = R$ then $z_{ρ} [D] = [0, \infty]$ so success fails if $η = [0, 4]$ , because outcomes larger than 4 occur. But if disturbances are restricted to $D = [- 2, 2]$ then $z_{ρ} [D] = [0, 4]$ so success holds since $η = [0, 4]$ .

Case 2: $E$ is an evaluative space distinct from the y-axis

If the y-axis shows fine-grained outcomes, while regulation cares only whether those outcomes are acceptable, then define

E = {acceptable, unacceptable}

with evaluation map

φ : Z \to E

φ (z) = {\begin{matrix} acceptable & if 0 \leq z \leq 4 \\ unacceptable & if z > 4 \end{matrix}}

Then the y-axis is still $Z$ but E is now a coarser evaluative variable and the acceptable subset is

η = {acceptable} \subseteq E

In this second case, E is not directly identical with the y-axis unless you add the extra evaluation layer. Rather, the y-axis is first mapped into an evaluative space by φ.

In one sentence, in the parabola example, the curve shows the mapping from disturbance-values to outcome-values; E appears only after you decide how those outcome-values are to be evaluated for survival or acceptability; and $η$ is the acceptable part of that evaluative space.

The Parabola as Possibility, and Realization as a Subset of Possibility

This full graph G the possible disturbance-outcome relation generated by the mapping.. Actuality appears only after a realized disturbance subset $D_{r} \subseteq D$ is specified.

Then the set of realized outcome-values is

Y = z (D_{r}) \subseteq Z

and the realized part of the graph is

G_{r} = {(d, z (d)) : d \in D_{r}} \subseteq G

Thus, the x-axis contains possible disturbance-values, the y-axis contains possible outcome-values, the full parabola represents the possible disturbance–outcome relation, and only a subset of its points need be realized in fact.

For example, if the realized disturbances are

D_{r} = {- 2, 0, 3}

then the realized outcome-values are

Y = {0, 4, 9}

not because these are all possible outcome-values, but because these are the values generated by the disturbances that actually occurred.

Example of a Human Knowledge Discovery Process with Goal-Model Revision

We now apply the same set-based structure to a simple human knowledge-discovery task: typing the word “Honorificabilitudinitatibus”.

The authoritative target word is:

Honorificabilitudinitatibus

It has 27 letters. Let $P = {1, ..., 27}$ be the set of target-word positions, and let $A$ be the set of possible typed symbols. Let $w_{i}$ denote the authoritative correct symbol at position $i$ in the target word.

Outcome-value space

The outcome-value space records what symbol was typed for what intended target position. Thus we define:

Z = P \times A

An outcome-value has the form:

z = (p, a) \in Z

where $p$ is the intended position in the target word, and $a$ is the typed symbol. For example, $(1, H)$ means that the symbol H was typed for position 1.

This is different from the closure-event index. The closure-event index $u$ records when the typing act occurred. The target-position index $p_{u}$ records which position the act attempted to satisfy. Therefore, $u \neq p_{u}$ in general.

Essential-variable space

In this example, both the outcome-value space and the essential-variable space are two-dimensional. The two dimensions are target-word position and symbol. Thus the outcome-value space has coordinates $(p, a)$ , and the essential-variable space uses the same two goal-relevant dimensions: which symbol occupies which target-word position for purposes of judging success.

There are two equivalent ways to read this example.

Reduced correspondence. In the reduced case, the concrete outcome-value is already the essential-variable value:

E = Z = P \times A

φ = {id}_{E}

So, in the reduced case:

z = (p, a) = e

Bijective correspondence. In the bijective case, the outcome-value space and the essential-variable space are conceptually distinct, but every relevant outcome-value corresponds to exactly one essential-variable value, and every relevant essential-variable value corresponds to exactly one outcome-value.

For the bijective reading, the outcome-value space and essential-variable space are conceptually distinct but have the same two-dimensional coordinate structure:

Z = P \times A

E = P_{E} \times A_{E}

where $P_{E}$ is the essential-variable coordinate for target position, and $A_{E}$ is the essential-variable coordinate for the symbol occupying that position. Thus an essential-variable value may be written as $e = (p, a)_{E}$ , where $e$ means: “the goal-relevant state in which symbol $a$ occupies target position $p$ .”

The outcome-to-essential-variable map is:

φ ((p, a)) = (p, a)_{E}

This map is bijective on the relevant modeled spaces. The concrete outcome $(p, a)$ and the essential-variable value $e_{p, a}$ are not the same object, but they carry the same distinctions for this regulatory model.

Authoritative acceptable essential-variable region

The authoritative acceptable essential-variable region is the set of goal-relevant states corresponding to the correct position-symbol pairs in the target word:

η^{*} := {e_{i, w_{i}} : i \in P} \subseteq E

For example:

e_{1, H} \in η^{*}

but:

e_{1, x} \notin η^{*} and e_{1, q} \notin η^{*}

The authoritative acceptable region does not change during the exercise. The target word remains the same. The Shakespeare text did not change. The required symbol at position $i$ did not change.

Authoritative acceptable outcome-set

The authoritative acceptable outcome-set is the pullback of the authoritative acceptable essential-variable region along $φ$ :

O^{*} := φ^{- 1} [η^{*}]

In the bijective case, this gives:

O^{*} = {(i, w_{i}) : i \in P} \subseteq Z

In the reduced case, since $φ = {id}_{E}$ , the same condition reduces to:

O^{*} = η^{*}

Thus the example can be read either way. In the reduced reading, outcome-values already are essential-variable values. In the bijective reading, outcome-values and essential-variable values are conceptually distinct but informationally equivalent under $φ$ .

Believed acceptable outcome-set

The typist does not initially know the authoritative acceptable outcome-set perfectly. At time $t$ , the typist acts under a believed model of the acceptable essential-variable region:

\hat{η}_{t} \subseteq E

This induces the typist's believed acceptable outcome-set:

\hat{O}_{t} := φ^{- 1} [\hat{η}_{t}]

In the reduced representation:

\hat{O}_{t} = \hat{η}_{t}

From the typist's subjective perspective, an incorrect symbol may initially appear to belong to the acceptable outcome-set. Later checking against the authoritative word reveals that it does not. This is not external goal revision, because $η^{*}$ and $O^{*}$ remain fixed. What changes is the typist's believed model: $\hat{η}_{t}$ and therefore $\hat{O}_{t}$ .

That is goal-model revision, not goal revision.

Closure events

Each typed symbol is a closure event:

c_{u} = (u, d_{u}, r_{u}, z_{u})

where:

$u$ is the closure-event index;
$d_{u}$ is the current demand to type a symbol for an intended target position;
$r_{u}$ is the selected keypress;
$z_{u}$ is the resulting typed outcome-value.

The produced outcome-value is:

z_{u} = (p_{u}, a_{u})

where $p_{u}$ is the intended target position and $a_{u}$ is the typed symbol.

For example:

					z₁ = (1, x)   provisionally accepted, later invalidated
					z₂ = (1, q)   provisionally accepted, later invalidated
					z₃ = (1, H)   survives authoritative checking
					z₄ = (2, o)   survives authoritative checking
					z₅ = (3, n)   survives authoritative checking

This preserves the distinction between event order and target position. Events 1, 2, and 3 are three different closure events, but all three attempt to satisfy position 1.

Operational trace

The following trace contains 37 typed closure events. The letters marked with 1 are the closure events that survive authoritative checking. The letters marked with 0 are provisional closure events that are later invalidated.

Closure event	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37
Target position pᵤ	1	1	1	2	3	4	5	6	6	7	8	9	10	11	12	13	13	13	14	15	16	16	17	18	19	19	19	20	21	21	21	22	23	24	25	26	27
Typed symbol aᵤ	x	q	H	o	n	o	r	e	i	f	i	c	a	b	i	o	r	l	i	t	m	u	d	i	p	v	n	i	y	k	t	a	t	i	b	u	s
Ledger status	0	0	1	1	1	1	1	0	1	1	1	1	1	1	1	0	0	1	1	1	0	1	1	1	0	0	1	1	0	0	1	1	1	1	1	1	1

Reading only the surviving closure events, the events marked 1, gives the final accepted output:

Honorificabilitudinitatibus

Reading the events marked 0 gives the provisional closures that were later rejected:

x, q, e, o, r, m, p, v, y, k

Provisional closure history

Let the observation window be:

I = (t_{a}, t_{b}]

A closure is provisionally accepted when produced if its outcome-value belongs to the typist's believed acceptable outcome-set at that time:

z_{u} \in \hat{O}_{u}

The provisional closure history in the window is:

C_{I}^{\hat{+}} := (c_{u} : t_{a} < u \leq t_{b}, z_{u} \in \hat{O}_{u})

In this example, all 37 typed symbols were provisionally accepted when produced. Therefore:

S_{gross}^{\hat{}} (I) := | C_{I}^{\hat{+}} | = 37

Authoritative survival and model invalidation

A provisional closure survives if its produced outcome-value belongs to the authoritative acceptable outcome-set:

z_{u} \in O^{*}

The net surviving closures are:

S_{net} (I) := # {c_{u} \in C_{I}^{\hat{+}} : z_{u} \in O^{*}} = 27

A provisional closure is invalidated by goal-model revision if it was accepted under the believed model when produced, but later judged outside the authoritative acceptable outcome-set:

z_{u} \in \hat{O}_{u} but z_{u} \notin O^{*}

The goal-model invalidation load is:

W_{model} (I) := # {c_{u} \in C_{I}^{\hat{+}} : z_{u} \notin O^{*}} = 10

Therefore the ledger identity is:

S_{gross}^{\hat{}} (I) = S_{net} (I) + W_{model} (I)

37 = 27 + 10

Interpretation

In the reduced case, the typed outcome-value already is the essential-variable value. In the bijective case, the typed outcome-value is a concrete outcome description, and the essential-variable value is the corresponding goal-relevant description.

In this example, the 10 invalidated events are actual typed outputs. Each one was a provisional closure produced under the typist's then-current belief i.e. their model of the goal. Later, after checking the authoritative word in the script, the typist discovered that those provisional closures did not belong to the authoritative acceptable outcome-set.

Quantity	Value	Meaning
$S_{gross}^{\hat{}} (I)$	37	All provisionally accepted typed closures.
$S_{net} (I)$	27	Typed closures that survived authoritative checking and form the final word.
$W_{model} (I)$	10	Typed closures invalidated after goal-model revision.

This ledger makes visible a kind of knowledge discovery process: acting from an incorrect believed model, then discovering that some completed closures must be invalidated and replaced.

In this example, the authoritative goal did not change. The word to be typed remained the same. What changed was the regulator's model of the goal. The process therefore involved goal-model revision, invalidation of provisional closures, and corrective replacement, not external goal revision.

Knowledge To Be Discovered perspective

In this example, the demand space is $D_{τ} = {demand to type position p : p \in P}$ , rthe esponse space is $R_{τ} = A$ , because the concrete response is the selected keypress or typed symbol $r_{u} = a_{u} \in A$ . The closure outcome records that response together with the intended target position: $z_{u} = (p_{u}, a_{u}) \in P \times A$ . For knowledge accounting, we use the lifted response-equivalence space $X_{τ} = P \times A$ , where the response class is represented together with the target position, because the required response-class is not merely a symbol, but a symbol-for-a-position, because the closure records which symbol was typed for which intended position.

The task class $τ_{letter}$ is: type the correct symbol for a target-word position in “Honorificabilitudinitatibus.” Under that task class, every closure event in the trace is one episode of the same regulatory problem: given a target position p, determine and emit the authoritative symbol required at that position. Thus all closure events in the example are comparable under the same task class $τ_{letter}$ They share the same disturbance space $P$ , the same concrete response space $A$ , the same outcome space $P \times A$ , and the same lifted target response-class space $X_{τ} = P \times A$ .

This example makes explicit why Knowledge To Be Discovered should be defined over the authoritative target response-class, not over the actual response-class emitted by the regulator. The typist produces actual closures, but those closures are not automatically the closures required by the authoritative goal.

For a closure event $u$ , the actual produced outcome-class is:

X_{u} = z_{u} = (p_{u}, a_{u})

where $p_{u}$ is the intended target position and $a_{u}$ is the symbol actually typed.

But the authoritative target response-class for that same event is:

X_{u}^{*} = (p_{u}, w_{p_{u}})

where $w_{p_{u}}$ is the authoritative symbol required at the intended target position.

Thus the central distinction is:

X_{u} = what the typist actually produced

X_{u}^{*} = what the authoritative goal required

Knowledge To Be Discovered is the remaining uncertainty, given the typist's current information state, about the authoritative target response-class:

Knowledge To Be Discovered = H_{M_{t}} (X_{t}^{*} | Y_{u})

In the generic time-indexed notation used elsewhere, this is:

Knowledge To Be Discovered = H_{M_{t}} (X_{t}^{*} | Y_{t})

Here $Y_{t}$ represents the disturbance, observation, or demand presented to the regulator at time $t$ . In this example, $Y_{u}$ can be read as the current demand to type the symbol for target position $p_{u}$ . The typist's current knowledge, memory, belief, and goal-model state is represented separately by $M_{t}$ .

The subscript $M_{t}$ means that the entropy is evaluated relative to the regulator's current model. The conditioning variable $Y_{t}$ specifies the disturbance or demand currently being faced. In this example, the demand may identify the target position, while the model $M_{t}$ determines how much uncertainty remains about the authoritative symbol required at that position.

In this example, if the typist is attempting to satisfy position 1, the authoritative target response-class is:

X^{*} = (1, H)

But the actual produced response-classes were:

							X₁ = (1, x)   actual closure, later invalidated
							X₂ = (1, q)   actual closure, later invalidated
							X₃ = (1, H)   actual closure, survives authoritative checking

Therefore:

X_{1} \neq X_{1}^{*}

X_{2} \neq X_{2}^{*}

X_{3} = X_{3}^{*}

This is why the strong alignment assumption:

X_{t} = X_{t}^{*}

does not hold during this knowledge-discovery process. The typist's actual closures are not yet reliably aligned with the authoritative target closures. Some actual closures are exploratory, mistaken, provisional, or based on an incorrect believed goal model.

Consequently, the entropy of the actual response-class:

H_{M_{t}} (X_{t} | Y_{t})

does not necessarily measure Knowledge To Be Discovered. It measures residual variation in what the regulator actually does. That variation may come from several sources: randomness, indecision, exploration, implementation variation, motor error, or even consistently wrong behavior. From an outside black-box perspective, these sources are not directly separable merely by observing the emitted closures.

By contrast:

H_{M_{t}} (X_{t}^{*} | Y_{t})

measures uncertainty about the target response-class that would satisfy the authoritative goal. That is the knowledge the regulator must acquire, infer, retrieve, or otherwise make available in order to close the demand correctly.

Why the ledger is evidence of discovery, not the entropy itself

The closure ledger:

37 = 27 + 10

is not itself an information-theoretic entropy identity. It is an operational accounting identity:

$provisional closures = surviving closures + invalidated closures$

The 10 invalidated closures are not 10 bits of Knowledge To Be Discovered. They are observable consequences of acting before the relevant target knowledge was fully available. They show that the typist's believed model allowed closures that the authoritative goal later rejected.

Thus:

W_{model} (I) = 10

measures model-invalidation load, not Knowledge To Be Discovered directly. It is a trace left by knowledge discovery in the closure history. The entropy measure remains:

H_{M_{t}} (X_{t}^{*} | Y_{t})

because the unresolved question is not merely “what will the typist type?” but “what response-class is required for authoritative success, given what the typist currently knows?”

Role of goal-model revision

The authoritative goal does not change in this example. The word remains:

Honorificabilitudinitatibus

Therefore $O^{*}$ and $η^{*}$ remain fixed. What changes is the typist's believed model:

\hat{O}_{t}, \hat{η}_{t}

This is why the process is goal-model revision, not external goal revision. The typist discovers that the believed acceptable outcome-set was too permissive. After checking, some provisional closures are removed from the believed acceptable region, and replacement closures are produced.

From the Knowledge To Be Discovered perspective, checking the authoritative word changes the information state:

Y_{t} \to Y_{t + 1}

and therefore can reduce:

H_{M_{t}} (X_{t}^{*} | Y_{t})

When the typist finally knows that position 1 requires H, the uncertainty about the authoritative response-class for that position collapses:

H_{M_{t}} (X^{*} | Y = (1, H) is known) = 0

At that point, no further knowledge must be discovered for that particular target-position closure. The remaining task is execution: producing the known required response.

Why this example supports the present definition

This example supports the definition:

Knowledge To Be Discovered := H (X_{t}^{*} | Y_{t})

because the discovered knowledge is knowledge about the target response-class required for successful regulation. The target is not whatever the regulator happens to emit. The target is the authoritative closure that would place the outcome inside the acceptable region.

The actual response-class $X_{t}$ can be wrong, exploratory, random, inconsistent, or provisionally accepted under a mistaken model. Therefore:

H (X_{t} | Y_{t}) \neq Knowledge To Be Discovered

in the general case.

Only under the strong alignment assumption:

X_{t} = X_{t}^{*}

does the actual response-class entropy coincide with target response-class uncertainty:

H (X_{t} | Y_{t}) = H (X_{t}^{*} | Y_{t})

This example is valuable precisely because it shows that the strong alignment assumption fails during knowledge discovery. The typist does not begin with perfect knowledge of the authoritative target closure. The typist emits closures, invalidates some of them, revises the believed goal model, and eventually aligns actual closures with authoritative target closures.

The example therefore serves as a reference case for why Knowledge To Be Discovered is H(X_t^*|Y_t): the uncertainty that matters is uncertainty about the authoritative target closure, not merely variation in the closures actually produced.

A Realized Knowledge Discovery Trace

This example shows how a concrete execution trace can be used to estimate the amount of knowledge discovered during a task. The purpose of the example is not to estimate the entropy of English, nor the entropy of a word. The purpose is to make visible the knowledge-discovery burden experienced during one realized execution of one task.

The Task

Consider the task of typing the word “Honorificabilitudinitatibus” on a keyboard. The word has 27 letters. The manual part of the task is to press the correct keys. The knowledge part of the task is to know which 27 letters must be typed, and in which order.

In this example, the typist does not remember the whole word at once. Sometimes the next required letter is already available from memory. At other times, the typist has to stop, think, or look up the word again. We record this process with a binary trace:

1 means the required next letter was already available for action.
0 means the typist was missing information and had to ask a question, think, or look up the word before continuing.

Thus, the letters typed are the surviving closures of the process, while the zeros are the counted missing-information intervals required to produce those closures.

The Observed Trace

The realized trace can be summarized as follows:

Segment	Trace	Questions $Q_i$	Typed letters $S_i$	Missing information $H_i = Q_i / S_i$	Total intervals $N_i = Q_i + S_i$
Initial lookup and first remembered chunk	`00 11111`	2	5	2/5	7
Second remembered chunk	`0 1111111`	1	7	1/7	8
Third remembered chunk	`00 111`	2	3	2/3	5
Fourth remembered chunk	`0 111`	1	3	1/3	4
Fifth remembered chunk	`00 11`	2	2	2/2	4
Final remembered chunk	`00 1111117`	2	7	2/7	9
Total	Realized execution trace	$\sum Q_i = 10$	$\sum S_i = 27$		$\sum N_i = 37$

There are 27 typed letters and 10 counted missing-information intervals. Therefore:

\[ Q = 10,\qquad S_{net} = 27,\qquad N = Q + S_{net} = 37. \]

Aggregating Missing Information Across Subsets

The trace can also be analyzed by decomposing the task into six subsets. Each subset has its own number of questions $Q_i$, its own number of typed symbols $S_i$, and therefore its own local missing-information value:

\[ H_i = \frac{Q_i}{S_i}. \]

However, the total missing information for the whole task is not obtained by simply summing the six $H_i$ values, nor by taking their unweighted arithmetic average. The subsets have different sizes. A subset of seven typed symbols must contribute more to the aggregate value than a subset of two typed symbols.

Therefore, the aggregate missing information is computed as a weighted average, where each local value $H_i$ is weighted by the proportion of symbols in that subset:

$H = \frac{\sum_{i = 1}^{n} Q_{i}}{\sum_{i = 1}^{n} S_{i}} = \frac{1}{\sum_{i = 1}^{n} S_{i}} \sum_{i = 1}^{n} Q_{i} = \frac{1}{S} \sum_{i = 1}^{n} (N_{i} - S_{i}) = \frac{1}{S} \sum_{i = 1}^{n} S_{i} (\frac{N_{i} - S_{i}}{S_{i}}) = \frac{1}{S} \sum_{i = 1}^{n} S_{i} (\frac{N_{i}}{S_{i}} - 1) = \frac{1}{S} \sum_{i = 1}^{n} S_{i} H_{i} .$

Here:

$n$ is the number of subsets;
$S_i$ is the number of typed symbols in subset $i$;
$Q_i$ is the number of questions in subset $i$;
$H_i = Q_i/S_i$ is the missing information in subset $i$;
$N_i = Q_i + S_i$ is the total number of intervals in subset $i$;
$S = \sum_{i=1}^{n} S_i$ is the total number of typed symbols.

Using the six subsets from the table:

$H = \frac{1}{S} \sum_{i = 1}^{n} S_{i} H_{i} = \sum_{i = 1}^{n} \frac{S_{i}}{S} \frac{Q_{i}}{S_{i}} = \frac{5}{27} \times \frac{2}{5} + \frac{7}{27} \times \frac{1}{7} + \frac{3}{27} \times \frac{2}{3} + \frac{3}{27} \times \frac{1}{3} + \frac{2}{27} \times \frac{2}{2} + \frac{7}{27} \times \frac{2}{7} = \frac{10}{27} \approx 0.37 .$

So the aggregate missing information remains $0.37$ missing-information units per typed symbol. The subset calculation gives the same result as the direct calculation, but it makes clear why the local $H_i$ values must be weighted by subset size.

Subset missing-information values cannot be added directly. The correct aggregate is the symbol-weighted average: $H = \frac{1}{S}\sum_{i=1}^{n}S_iH_i$.

The Operational Estimator

The effective one-bit-equivalent Knowledge To Be Discovered over this interval is:

\[ \widehat{KTD}_{eff}^{1bit,net}(I) = \frac{N(I)}{S_{net}(I)} - 1. \]

Substituting the observed values gives:

\[ \widehat{KTD}_{eff}^{1bit,net}(I) = \frac{37}{27} - 1 = \frac{10}{27} \approx 0.37. \]

So, in this realized execution, the typist needed approximately 0.37 counted missing-information units per typed symbol.

This number is an operational one-bit-equivalent estimate. It is exact as a ratio over the observed trace, but it should not be confused with the Shannon entropy of English or the entropy of the word itself.

Why This Corresponds to $H(X \mid Y = y_u)$

The important point is that this calculation is based on the actual observed knowledge state of the typist during the task. We are not averaging over all possible memory states, all possible words, or all possible observations. We are looking at the realized case: this typist, this word, this sequence of remembered and forgotten chunks.

For that reason, the corresponding latent quantity is the realized row-level conditional uncertainty:

\[ H_u^{start} := H_{M_u}(X_u \mid Y_u = y_u). \]

Here, $X_u$ is the required response-equivalence class for closure event $u$, and $Y_u = y_u$ is the actual knowledge state available at the start of that episode. The estimator uses the realized value $y_u$, not the full distribution of possible values of $Y_u$.

By contrast, $H_{M_u}(X_u \mid Y_u)$ would be an ex-ante quantity. It would require a probability distribution over possible knowledge states before the realized state is known. That is not what the trace records. The trace records what actually happened.

The operational ledger estimates realized Knowledge To Be Discovered:

H (X ∣ Y = y_{u})

The theoretical quantity

H (X ∣ Y)

belongs to an ex-ante model that averages over possible observation states.

What if $E$ changes?

The above definitions assume that the essential-variable space $E$ and the outcome-to-essential-variable map $φ$ are held fixed. Under that assumption, addition, deletion, and substitution are changes in acceptability-status caused by a change in the acceptable region $η$ .

if $E$ changes, then the logic changes conceptually. This is not merely a different acceptable region. It is a different evaluative model: different dimensions of what counts as goal-relevant.

That matters because Ashby treats the system as a set of variables selected for analysis; changing the selected variables changes the modeled system/criterion, not just the acceptable subset. Ashby's framework is explicitly functional and behavior-oriented rather than material-object-oriented, so the selected variables are part of the formal description[1]. Umpleby also emphasizes that, for Ashby, the “system” is a set of variables selected by an observer[57].

If the essential-variable space itself changes, then the change is no longer merely a revision of the acceptable region. It is a change in the evaluative model. In that more general case, one would write $φ_{t} : Z \to E_{t}$ and $η_{t} \subseteq E_{t}$ . The acceptable outcome-set would still be comparable across time if the outcome-space $Z$ remains fixed:

O_{acc, t} := φ_{t}^{- 1} [η_{t}] \subseteq Z

In that case, deletion, addition, and substitution can still be defined as set differences inside $Z$ , but their interpretation changes: they may result from a changed acceptable region, a changed essential-variable space, a changed mapping from outcomes to essential variables, or some combination of these.

If the outcome-space $Z$ remains fixed, then we can still define:

O_{acc, t_{1}} := φ_{t_{1}}^{-1} [η_{t_{1}}] \subseteq Z

O_{acc, t_{2}} := φ_{t_{2}}^{-1} [η_{t_{2}}] \subseteq Z

Now both acceptable outcome-sets are again subsets of the same $Z$ , so our deletion/addition/substitution logic still works.

L_{12} = O_{acc, t_{1}} ∖ O_{acc, t_{2}}

G_{12} = O_{acc, t_{2}} ∖ O_{acc, t_{1}}

P_{12} = O_{acc, t_{1}} \cap O_{acc, t_{2}}

But the interpretation is different.

The change may now be caused by:

a changed acceptable region $η_{t}$
a changed essential-variable space $E_{t}$
a changed outcome-to-essential-variable map $φ_{t}$
or some combination of the above.

So we can still say: outcome-value z lost acceptability, but we should not say: z lost acceptability only because the goal region changed.

It may have lost acceptability because the system is now being evaluated through different essential variables.

Example

At $t_{1}$ , suppose success is evaluated only by temperature:

E_{t_{1}} = E_{temp}

At $t_{2}$ , success is evaluated by temperature and blood sugar:

E_{t_{2}} = E_{temp} \times E_{glucose}

An outcome z that was acceptable at $t_{1}$ may become unacceptable at $t_{2}$ , not because the acceptable temperature range changed, but because blood sugar is now included as a goal-relevant dimension.

So the outcome has been “deleted” from the acceptable outcome-set, but this deletion comes from a change in evaluation space, not merely a narrower acceptable region.

In summary, changing $E$ does not destroy the deletion/addition/substitution logic if we compare pulled-back acceptable outcome-sets inside the same fixed $Z$ . But it changes the meaning of those changes. They are no longer purely goal-region revisions; they may be changes in the evaluative model itself.

What learning could also do (but we are explicitly excluding)

Not every form of learning improves regulation H(E|Y) in Ashby's sense. Other possibilities include:

Expanding action variety without selectivity
Learning might increase $H (X)$ (more possible actions, tools, behaviors) without reducing $H (X | Y)$ .
- The system becomes more capable in principle
- But still does not know which action to take
- Regulation does not improve
This violates Ashby's requirement that variety must be constrained, not merely expanded.
Improving buffering instead of knowledge
Learning might increase buffering capacity $q$ (delay, slack, tolerance), so disturbances are absorbed without better action selection.
- Outcomes may improve
- But $I (X : Y)$ does not increase
- Regulation improves without learning the mapping
This is explicitly separated from knowledge in Ashby's extended formulation.
Changing goals or success criteria
Learning could redefine what counts as success $E$ .
- Apparent performance improves
- But the structural coupling (mapping) is unchanged
- Information-theoretically, nothing about $H (X | Y)$ need change
This is semantic drift, not cybernetic learning.
One-off adaptation without structural retention
The system may succeed through exploration $Z$ without storing the result.
- Regulation succeeds this time
- Next encounter repeats the same uncertainty
- No accumulation of $I (X : Y)$
This is regulation, not learning.

Cumulative Knowledge To Be Discovered

Using

H (S) = \frac{N}{S} - 1

from (5) with constant

N

, the cumulative residual variety (C) as a function of performance level (S) has a clean closed form.

Cumulative w.r.t. S
Choose a baseline $S_{0}$ > 0.
Define:

C (S; S_{0}) = \int S_{0} S H (u) d u = \int S_{0} S (\frac{N}{u} - 1) d u = N ln \frac{S}{S_{0}} - (S - S_{0}) .

Key properties:

$\frac{d C}{d S} = H (S) = \frac{N}{S} - 1$
$\frac{d^{2} C}{d^{2} S} = - \frac{N}{S^{2}} < 0$ → $C$ is concave in $S$ .

Domain: $S$ ∈ (0, N]. Since $H (S)$ > 0 for $S < N$ , $C (S; S_{0})$ increases with $S$ (for $S \geq S_{0}$ ) and is finite as long as $S_{0} > 0$ .

Useful normalizations:
Dimensionless form with $\hat{S} = \frac{S}{N}$ : $\frac{C (\hat{S}; {\hat{S}}_{0})}{N} = ln \frac{\hat{S}}{{\hat{S}}_{0}} - (\hat{S} - {\hat{S}}_{0}) .$

Total cumulative up to completion S = N: $C (N; S_{0}) = N \cdot ln (\frac{N}{S_{0}}) - (N - S_{0}) .$

This can be thought of as the total knowledge-effort curve or “cumulative residual variety as a function of performance level” i.e. how much “knowledge work” has been consumed to reach performance level S.

**Fig.2 Total Knowledge-Effort Curve** Here we see the cumulative residual variety as a function of performance level.

Blue curve: instantaneous 𝐻(𝑆)=𝑁/𝑆−1H(S)=N/S−1 (residual variety ratio).

Green dashed curve: cumulative residual variety C(S) as we accumulate uncertainty over growing performance level S.

Each point on the curve says “At performance level S, there are *H(S)* bits of uncertainty to be eliminated for perfect regulation.” We can see how H(S) declines hyperbolically, while C(S) rises concavely.

How to cite:

Bakardzhiev D.V. (2025) Knowledge Discovery Efficiency (KEDE) and Ashby's Law https://docs.kedehub.io/knowledge-centric-research/kede-ashbys-law.html

Works Cited

1. Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal. 1948;27(3):379-423. doi:10.1002/j.1538-7305.1948.tb01338.x

2. Ashby, W.R. (1956). An Introduction to Cybernetics; Chapman & Hall,

3. Ashby, W. R. (2011). Variety, Constraint, And The Law Of Requisite Variety. 13, 18.

4. MacKay, D. M. (1950). Quanta! aspects of scientific information. Philosophical Magazine; 41, 289-311;

5. Cover, T. M. and Thomas, J. A. (1991), Elements of Information Theory, John Wiley and Sons, New York. page.95 in 5.7 SOME COMMENTS ON HUFFMAN CODES

6. Wheeler, J. A. (1990). Information, physics, quantum: The search for links. In W. H. Zurek (Ed.), Complexity, entropy, and the physics of information (Vol. 8, pp. 3'-28). Taylor & Francis.

7. Yaneer Bar-Yam.(2004) Multiscale variety in complex systems. Complexity, 9(4):37{45,

8. Ashby, W.R. (1991). Requisite Variety and Its Implications for the Control of Complex Systems. In: Facets of Systems Science. International Federation for Systems Research International Series on Systems Science and Engineering, vol 7. Springer, Boston, MA. https://doi.org/10.1007/978-1-4899-0718-9_28

9. Shannon, C. E. Communication theory of secrecy systems. Bell System technical Journal, 28, 656-715, 1949

10. Kubatko J, Oliver D, Pelton K, et al. A starting point for analyzing basketball statistics. J Quant Anal Sports 2007; 3: 1'-22.

11. Sports Reference LLC. "NBA League Averages." Basketball-Reference.com - Basketball Statistics and History. https://www.basketball-reference.com/leagues/NBA_stats_totals.html.

12. Bucks post highest single-game field-goal percentage by any team in 21st century https://sports.yahoo.com/article/bucks-post-highest-single-game-040313061.html

13. https://www.statmuse.com/nba/ask/most-field-goals-made-record-in-a-game-nba-player

14. Lewis, G. J., & Stewart, N. (2003). The measurement of environmental performance: an application of Ashby's law. Systems Research and Behavioral Science, 20(1), 31'-52. https://doi.org/10.1002/sres.524

15. Norman, J., & Bar-Yam, Y. (2018). Special Operations Forces: A Global Immune System? In Springer Unifying Themes in Complex Systems IX (pp. 486'-498). Springer International Publishing. https://doi.org/10.1007/978-3-319-96661-8_50

16. Norman, J., & Bar-Yam, Y. (2019). Special Operations Forces as a Global Immune System. In Springer Evolution, Development and Complexity (pp. 367'-379). Springer International Publishing. https://doi.org/10.1007/978-3-030-00075-2_16

17. O'Grady, W., Morlidge, S., & Rouse, P. (2014). Management Control Systems: A Variety Engineering Perspective. SSRN Electronic Journal. https://doi.org/10.2139/ssrn.2351099

18. Love, T., & Cooper, T. (2007). Digital Eco-systems Pre-Design: Variety Analyses, System Viability and Tacit System Control Mechanisms. 2007 Inaugural IEEE-IES Digital EcoSystems and Technologies Conference, 452'-457. https://doi.org/10.1109/dest.2007.372013

19. Love, T., & Cooper, T. (2007). Complex built‐environment design: four extensions to Ashby. Kybernetes, 36(9/10), 1422'-1435. https://doi.org/10.1108/03684920710827391

20. Bushey, D. B., & Nissen, M. E. (1999). A Systematic Approach to Prioritizing Weapon System Requirements and Military Operations Through Requisite Variety. Defense Technical Information Center. https://doi.org/10.21236/ada371943

21. Jones, H. P. (2018). Evolutionary stakeholder discovery: requisite system sampling for co-creation.

22. Grimm, D. A. P., Gorman, J. C., Robinson, E., & Winner, J. (2022). Measuring Adaptive Team Coordination in an Enroute Care Training Scenario. Proceedings of the Human Factors and Ergonomics Society Annual Meeting, 66(1), 50'-54. https://doi.org/10.1177/1071181322661074

23. Becker Bertoni, V., Abreu Saurin, T., & Sanson Fogliatto, F. (2022). Law of requisite variety in practice: Assessing the match between risk and actors' contribution to resilient performance. Safety Science, 155, 105895. https://doi.org/10.1016/j.ssci.2022.105895

24. Tworek, K., Walecka-Jankowska, K., & Zgrzywa-Ziemak, A. (2019). Towards organisational simplexity — a simple structure in a complex environment. Engineering Management in Production and Services, 11(4), 43'-53. https://doi.org/10.2478/emj-2019-0032

25. Chester, M. V., & Allenby, B. (2022). Infrastructure autopoiesis: requisite variety to engage complexity. Environmental Research: Infrastructure and Sustainability, 2(1), 012001. https://doi.org/10.1088/2634-4505/ac4b48

26. van der Hoek, M., Beerkens, M., & Groeneveld, S. (2021). Matching leadership to circumstances? A vignette study of leadership behavior adaptation in an ambiguous context. International Public Management Journal, 24(3), 394'-417. https://doi.org/10.1080/10967494.2021.1887017

27. Ulrik, S., & Isabella, A. (2023). Variety versus speed: how variety in competence within teams may affect performance in a dynamic decision-making task.

28. Bakardzhiev, D., Vitanov, N.K. (2025). KEDE (KnowledgE Discovery Efficiency): A Measure for Quantification of the Productivity of Knowledge Workers. In: Georgiev, I., Kostadinov, H., Lilkova, E. (eds) Advanced Computing in Industrial Mathematics. BGSIAM 2022. Studies in Computational Intelligence, vol 641. Springer, Cham. https://doi.org/10.1007/978-3-031-76786-9_3

29. Heylighen, F., & Joslyn, C. (2001). Cybernetics and Second Order Cybernetics. In R. A. Meyers (Ed.), Encyclopedia of Physical Science and Technology, Eighteen-Volume Set, Third Edition (pp. 155-170). Academia Press. http://pespmc1.vub.ac.be/Papers/Cybernetics-EPST.pdf

30. Schwaninger, M., & Ott, S. (2024). What is variety engineering and why do we need it? Systems Research and Behavioral Science, 41(2), 235'-246. https://doi.org/10.1002/sres.2964

31. AULIN‐AHMAVAARA, A.Y. (1979), "THE LAW OF REQUISITE HIERARCHY", Kybernetes, Vol. 8 No. 4, pp. 259-266. https://doi.org/10.1108/eb005528

32. Wu, T., Dufford, A. J., Mackie, M. A., Egan, L. J., & Fan, J. (2016). The Capacity of Cognitive Control Estimated from a Perceptual Decision Making Task. Scientific Reports, 6, 34025.

33. Abuhamdeh S (2020) Investigating the “Flow” Experience: Key Conceptual and OperationalIssues. Front. Psychol. 11:158.doi: 10.3389/fpsyg.2020.00158

34. Automatic Screw Tightening Machine and Its Hidden Features

35. Keating, C. B., Katina, P. F., Jaradat, R., Bradley, J. M., & Hodge, R. (2019). Framework for improving complex system performance. INCOSE International Symposium, 29(1), 1218-1232. https://doi.org/10.1002/j.2334-5837.2019.00664.x

36. S. Engell (1985). An information-theoretical approach to regulation.

37. K. Kijima, Y. Takahara, B. Nakano (1986). ALGEBRAIC FORMULATION OF RELATIONSHIP BETWEEN A GOAL SEEKING SYSTEM AND ITS ENVIRONMENT.

38. W. Kickert, J. Bertrand, J. Praagman (1978). Some Comments on Cybernetics and Control. IEEE Transactions on Systems, Man and Cybernetics.

39. S. Engell (1985). Information-theoretical bounds for regulation accuracy. IEEE Conference on Decision and Control.

40. Hui Zhang, Youxian Sun (2003). Bode integrals and laws of variety in linear control systems. Proceedings of the 2003 American Control Conference, 2003.

41. R. Conant (1969). The Information Transfer Required in Regulatory Processes. IEEE Transactions on Systems Science and Cybernetics.

42. S. Engell (1987). Analysis of Regulation Problems based on Real-Time Rate-Distortion Theory. American Control Conference.

43. Hui Zhang, Youxian Sun (2003). Information theoretic limit and bound of disturbance rejection in LTI systems: Shannon entropy and H/sub /spl infin// entropy. SMC'03 Conference Proceedings. 2003 IEEE International Conference on Systems, Man and Cybernetics. Conference Theme - System Security and Assurance (Cat. No.03CH37483).

44. N. C. Martins, M. Dahleh (2008). Feedback Control in the Presence of Noisy Channels: “Bode-Like” Fundamental Limitations of Performance. IEEE Transactions on Automatic Control.

45. Hui Zhang, Youxian Sun (2003). H/sub /spl infin// entropy and the law of requisite variety. 42nd IEEE International Conference on Decision and Control (IEEE Cat. No.03CH37475).

46. Tsuji, M., Crookshank, M., Olsen, M., Schemitsch, E. H., & Zdero, R. (2013). The biomechanical effect of artificial and human bone density on stopping and stripping torque during screw insertion. Journal of the mechanical behavior of biomedical materials, 22, 146'-156. https://doi.org/10.1016/j.jmbbm.2013.03.006

47. Akizuki, K., & Ohashi, Y. (2015). Measurement of functional task difficulty during motor learning: What level of difficulty corresponds to the optimal challenge point?. Human movement science, 43, 107'-117. https://doi.org/10.1016/j.humov.2015.07.007

48. Bootsma, J. M., Hortobágyi, T., Rothwell, J. C., & Caljouw, S. R. (2018). The Role of Task Difficulty in Learning a Visuomotor Skill. Medicine and science in sports and exercise, 50(9), 1842'-1849. https://doi.org/10.1249/MSS.0000000000001635

49. Akizuki, K., & Ohashi, Y. (2013). Changes in practice schedule and functional task difficulty: a study using the probe reaction time technique. Journal of physical therapy science, 25(7), 827'-831. https://doi.org/10.1589/jpts.25.827

50. Goldhammer, F.; Naumann, J.; Stelter, A.; Tóth, K.; Rölke, H.; Klieme, E.: The time on task effect in reading and problem solving is moderated by task difficulty and skill. Insights from a computer-based large-scale assessment - In: The Journal of educational psychology 106 (2014) 3, S. 608-626 - URN: urn:nbn:de:0111-pedocs-179679 - DOI: 10.25656/01:17967; 10.1037/a0034716

51. Boothroyd, G., and P. Dewhurst, "DESIGN FOR ASSEMBLY", Dept. of Mechanical Engineering, University of Massachusetts, Amherst, Massachusetts, 1983.

52. Jahin, A., Zidan, A. H., Bao, Y., Liang, S., Liu, T., & Zhang, W. (2025). Unveiling the mathematical reasoning in deepseek models: A comparative study of large language models. arXiv preprint arXiv:2503.10573.

53. FrontierMath: A Benchmark for Evaluating Advanced Mathematical Reasoning in AI

54. Francis Heylighen, Cybernetic Principles of Aging and Rejuvenation: The Buffering- Challenging Strategy for Life Extension, Current Aging Science; Volume 7, Issue 1, Year 2014, . DOI: 10.2174/1874609807666140521095925

55. Ostry, D. J. (1980). Execution-time movement control. In G. E. Stelmach & J. Requin (Eds.), Tutorials in motor behavior (pp. 457-468). Amsterdam: North-Holland.

56. Siegenfeld, A. F., & Bar-Yam, Y. (2025). A Formal Definition of Scale-Dependent Complexity and the Multi-Scale Law of Requisite Variety. Entropy, 27(8), 835. https://doi.org/10.3390/e27080835

57. Umpleby, S. A. (2009). Ross Ashby's general theory of adaptive systems. International Journal of General Systems, 38(2), 231–238. https://doi.org/10.1080/03081070802601509

Getting started

Frequently Asked Questions

About KEDE and KEDEHub

KEDEHub Features

All we need to analyze the efficiency of your organization

Knowledge-Centric Metrics

The complete set of concepts, terms and theories

Need help?

KEDEHub Documentation

Knowledge Discovery Efficiency (KEDE) and Ashby's Law of Requisite Variety

Related Articles

Abstract

Introduction

Core challenges in applying Ashby's Law to real systems

Solution

The Law of Requisite Variety

Set-based formulation

Requisite variety

Outcome map induced by a response rule at time t

Goal revision with fixed table and time-indexed acceptable outcomes

Revision of acceptability: deletion, addition, and substitution within the acceptable outcome-set

Strict substitution

Behavioral rework

Information-Theoretic Formulation

Random variables over the set-based regulatory geometry

Entropy, variety, and the outcome-to-essential-variable map

Probabilistic success and support-level success

Allowed residual variety

Response-equivalence and regulatory ignorance

Regulator's learned law of action

Knowledge To Be Discovered

Knowledge To Be Discovered and effective regulatory knowledge

Ashby-style residual-variety bounds

Point regulation

Knowledge Discovery Process

Set-based Formulation of Staged Selection

Action-unit protocols as partition-refinement updates

Rule regulation

Episodes and Closures

Count-Variety Selection

Information-Theoretic Formulation of Staged Selection

What the Information-Theoretic Model Adds

Notation and Modeling Assumptions

Staged Action Units and Realized Signals

Expected Staged Reduction of Knowledge To Be Discovered

Realized Conditioning Path Inside One Episode

Expected Selection Induced by the Action Protocol

Bridge to the Set-Based Candidate Trace

Lemma — Episode-Level Action-Unit Bridge

Bridge Lemma

Action Units, Signals, and Response-Class Commitment

Success, Closure, and Policy-Level Success

Summary

Learning (across episodes in a window)

Comparable episodes

Learning as stored transformation

From staged discovery to stored learning

Across-episode comparison of stored coupling

Learning axiom

Strong learning: posterior becomes prior

Learning, goal revision, and behavioral revision

Knowledge Discovery Accounting

Operational ledger

Closure events

Window

Gross counted closures

Historically realized outcome-set

Continuously surviving counted closures through the window

Invalidation load

Interpretation

Operational ledger for goal-model revision

Authoritative and believed acceptability

Provisional closure events

Provisional closure history

Gross provisional closures

Net surviving closures

Goal-model invalidation load

Ledger identity

Model-revision events

Corrective replacement

Relation to the criterion-revision ledger

Interpretation

Operational counting of action units as Effective non-net-progress load

Knowledge ledger

Closure-indexed knowledge ledger

KTD states at closure boundaries

Within-episode discovery and retained learning

Knowledge ledger stock-flow identity

Relation to the operational ledger

Where are $E$ and its acceptable subset η?

Case 2: $E$ is an evaluative space distinct from the y-axis